fit_line_contour_xld拟合直线的五种算法的准确度比较

 

大家在网上搜索“fit_line_contour_xld”应该很容易就能发现这样的几行字：（没耐心看的话，可以直接看文末三行研究结论）

 

regression：回归，标准的最小二乘法拟合

huber：加权的最小二乘法拟合，异常值的影响被减小基于Huber方法

tukey：加权的最小二乘法拟合，异常值的影响被减小基于Tukey方法（系统推荐方法）

gauss：加权的最小二乘法拟合，异常值的影响被减小基于最逼近线上的所有其轮廓点的平均值和距离标准方差

drop：加权的最小二乘法拟合，异常值的影响被消除

 

fit_line_contour_xld算子的签名如下：

 

fit_line_contour_xld(Contours : : Algorithm, MaxNumPoints, ClippingEndPoints, Iterations, ClippingFactor : RowBegin, ColBegin, RowEnd, ColEnd, Nr, Nc, Dist)

 

其中Algorithm参数可选择上面的5种算法之一。

如果有读者朋友图像处理理论基础深厚，自然知道每种算法拟合的准确度优劣和适应情况。但是就算不知道，也可以通过一定的方法研究得出结论。

 

 

我的研究方法如下：

 

① 找几十张有边可抓的图像。（待抓的边最好不要太直）

② 抓取图像的某一条边缘，抓边时会生成很多边缘交点，并生成最终拟合的直线。

③ 输出所有边缘交点到直线的距离，对这些距离进行从大到小排序。

④ 取第8号点（也可以取其他点，我这里拟合直线一共用了60个点）的值输出，命名为Offset，该值表示拟合的直线跟实际边缘点的近似最大偏差值。

 

分别采用 'regression'、'huber'、'tukey'、'gauss'、'drop'五种参数（Algortim算法）执行上述过程，并将每一张图的5个Offset值都输出到.csv文件中。

 

求出采用不同算法的每组数据的标准差，标准差越小，说明直线拟合准确度越高。（可以多测一些图片，多抓一些不同的边）

 

 

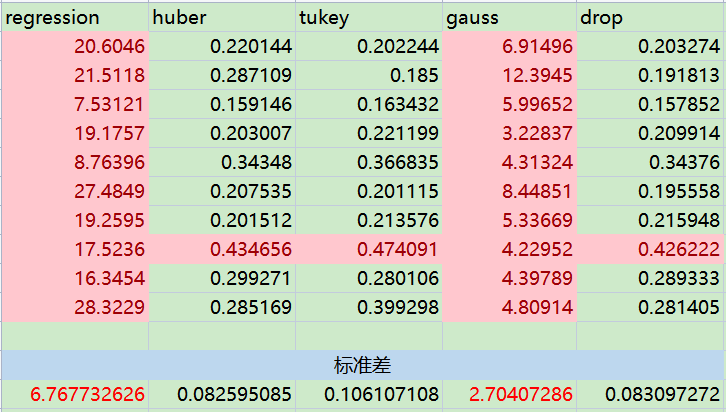
部分代码如下：

    get_image_size (ImageR, Width, Height)    
    gen_rectangle1 (Rect, 600, 0, Height - 600, 800)

    count_seconds (Seconds)
    find_line (ImageR, Rect, Line, Region1, Cross, 60, 8, 1, 12, 'positive', 'first', 'no', 5, Algortim)
    count_seconds (Seconds1)
  
    Time := (Seconds1 - Seconds) * 1000   
    
    area_center_xld(Cross, Area2, Row4, Column4, PointOrder)
    get_contour_xld(Line, row, col)
    distance_pl(Row4, Column4, row[0], col[0], row[1], col[1], Distance)
    
    tuple_sort(Distance, Sorted)
    tuple_inverse(Sorted, Inverted) //反转以后是从大到小排序
    
    Offset := Inverted[8]  //取第8号值是为了忽略偶然的极端值

注：拟合直线算子fit_line_contour_xld在第五行自己封装的find_line函数内部。

 

 

【研究结论】：

1、'regression'、'gauss'拟合效果很差，基本不用考虑。其他三种算法效果基本差不多。（五种算法的执行时间无明显差异）

2、少部分时候'tukey'拟合偏差有点大。虽然系统推荐的是'tukey'算法,，但经过我大量研究测试，效果最好的应该是'drop'。

3、如果非要对拟合准确度进行排序的话，那么我的结论是：'drop' > 'tukey' >≈ 'huber' > 'gauss' >> 'regression'。（>≈意思是左边的要好一些，但好得非常有限）