面向对象OO第一单元总结

面向对象第一单元总结

一、程序结构分析

第一次作业

第一次作业的要求为完成简单多项式的导函数求解，项包括变量因子和常数因子，其中变量因子只有幂函数,因此我只建造了三个类，分别为MainClass,Term和Expression。 其中MainClass类主要是控制输入字符串来生成Expression对象，而Exprssion类是用来解析字符串生成每个项Term，并且用HashMap来存储各个项的系数和指数的信息。Term类是用来返回每项的导函数的。类图如下：

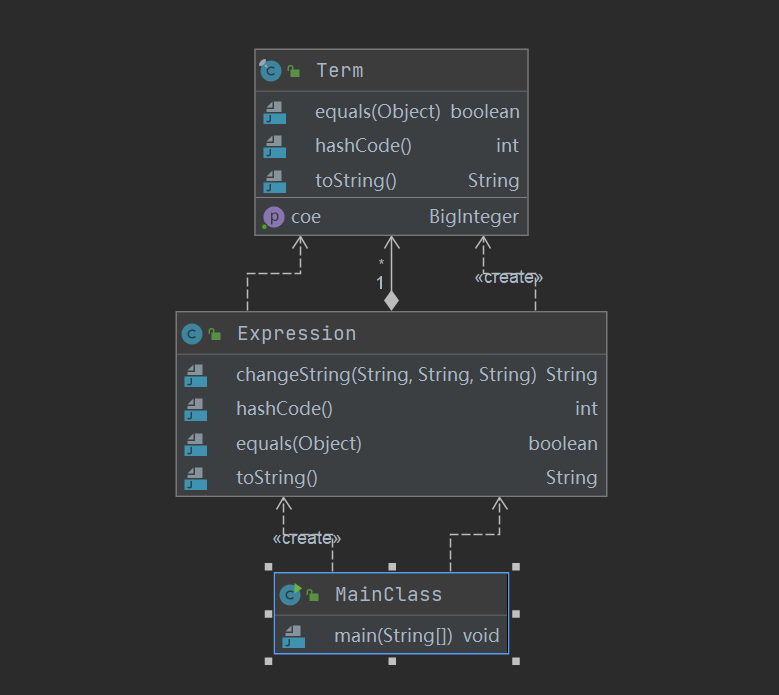
• MainClass类
  Main类的作用就是输入字符串来生成Expression对象，没有其他方法。
  
• Expression类
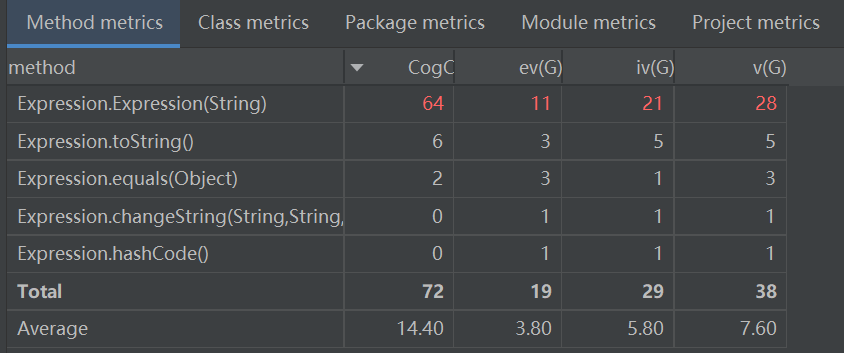
  Expression类通过调用Expression构造器，将字符串构造成一个个Item，将指数和系数存入map中，其中由于解析Item的过程中使用的算法未抽离出来，同时java的语法尚未了解清楚，故非常的面向过程，代码行数很多。为此，还专门写了一个changeString方法来进行字符串的相应替换，画蛇添足。
  在此类中，还对hashCode、equals和toString方法进行了重写，其中toString方法调用了map中Item类的toStirng方法，实现表达式的导函数输出。
  

可以看出，Expression方法的复杂度最高，方法规模也大。

• Term类
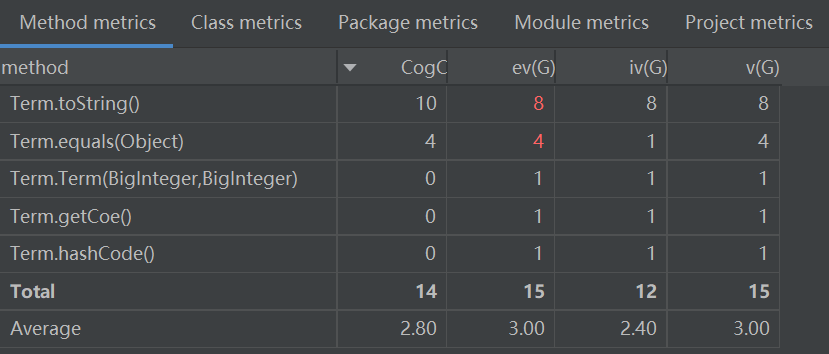
  Term类有含有四个方法，分别为重写的hashCode、重写的equal、输出相应项的导函数的toSting以及构造方法Term。
  
  同样，toString方法的复杂度最高。

优缺点分析

1. 优点
   • 思路简单
   • 对于0次系数等，通过Map有合并，对表达式进行了一定化简
2. 缺点
   • 方法冗长，重复代码过多。例如对于简单的格式替换，反复调用多次，既不便于检查，也不便于修改。
   • 代码风格极差。
   • 拓展性不强。对于之后的格式检查和嵌套规则，基本上这种正则表达式的构造方法很难有效进行功能拓展。

第二次作业

第二次作业需要完成的任务为包含简单幂函数和简单正余弦函数的导函数的求解。在第一次作业的基础上，增加了sin(x)和cos(x)这两个三角函数因子。这不仅带来因子的变化，还引入了新的求导规则。而在第一次作业中简单的多项式求导法则显然不能满足要求，因此我选择重构，将表达式用语法树来解析，再根据拆分出的叶子节点和其父节点的符号，来进行因子的求导和组合。
根据这个思路的类图如下：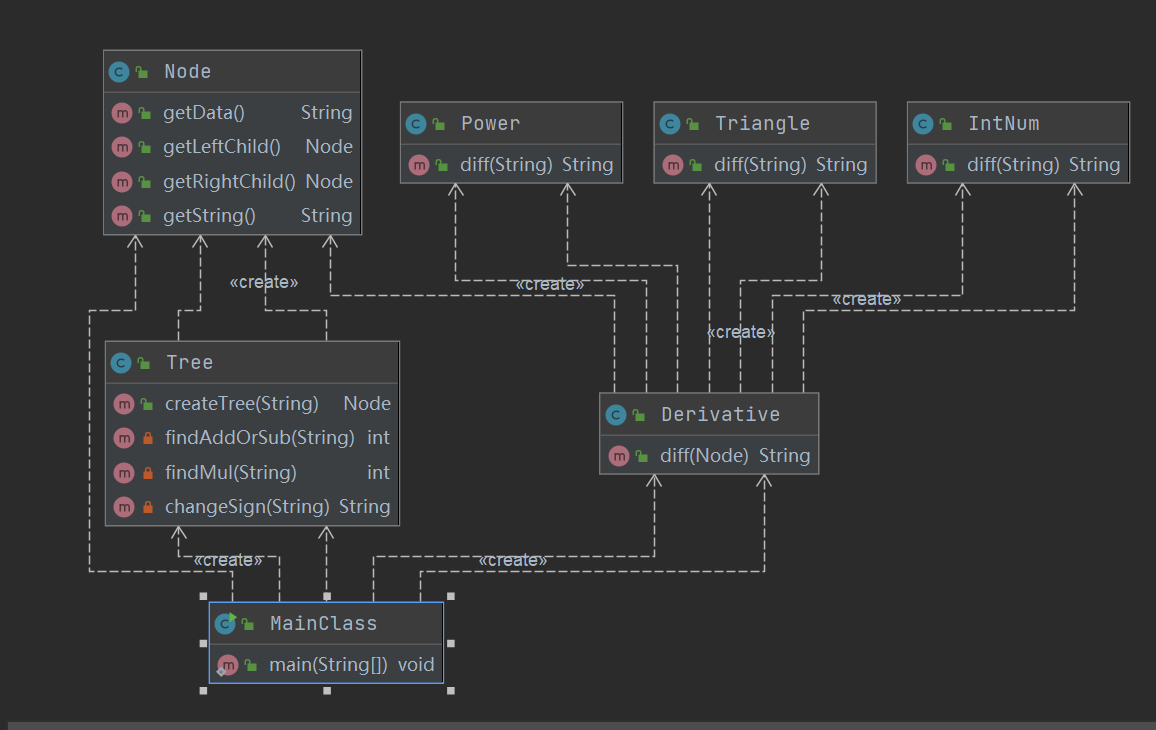

• MainClass
  由于没有格式检查，主类的功能没有多大变化，就是将表达式进行格式预处理之后，构造语法树。
  
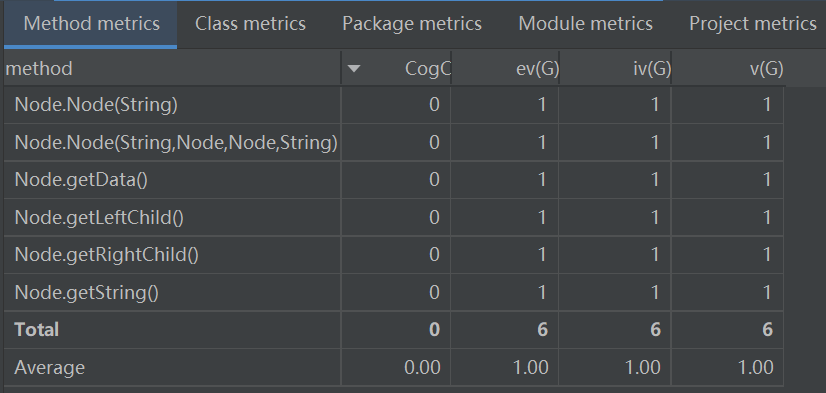
• Node
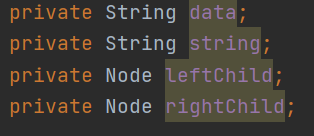
  这是语法树的结点类，包含了4个私有变量，分别为：
  其中，data用来存储符号，即表达式之间的+-或项之间的*，string用来存储项。其余两个分别为该结点的左右孩子。该类也定义了一些get方法来访问类中变量。
  
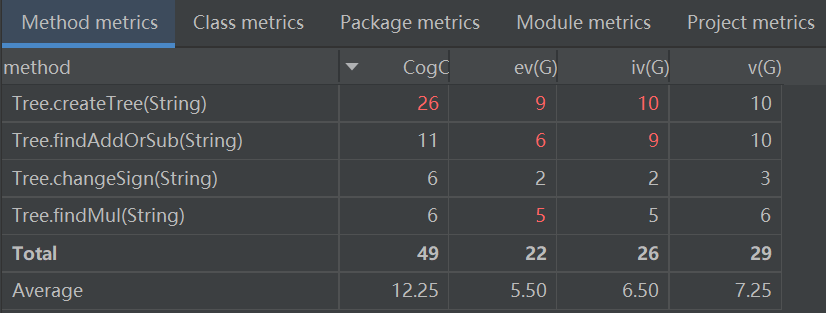
• Tree
  这是对语法树进行操作的类，包含有四个方法。其中createTree就是建造语法树的具体方法，它通过findAddOrSub方法和findMul方法找到符合条件的符号之后，通过changeSign方法将之后的项正确变号，生成一个二叉树。
• IntNum Power Triangle
  这三个类分别代表着常数因子、幂函数因子和三角函数因子。类中都带有一个方法diff来求对应因子的导函数。
  
• Derivative
  这是求导类，将树的根节点传入之后，根据Node类的data和string来识别对应因子创建相应的因子类，根据相应法则来进行导数组合。

优缺点分析

1. 优点
   • 采用语法树的构造方式，能有效分离各个因子或项，并对对应相应法则进行求导。
   • 有一定的拓展能力。
2. 缺点
   • 表达式由于嵌套括号的关系，会显得冗长。
   • 对于格式检查，只能重新分析。

第三次作业

第三次作业引入了简单正余弦函数及其嵌套组合函数的导函数的求解，还有格式检查。
对于嵌套组合函数而言，第二次的架构可以较为简单地修改，因为三角函数在语法树中是按叶子结点存储的，只需要将三角函数Triangle类中的求导方法中，对括号内的因子再次进行表达式树的构造，迭代之后即可表达出三角函数嵌套函数的导函数。
对于格式检查而言，引入了新类Gram来检查语法。检查语法采用递归下降的写法，根据形式性描述来验证表达式合法性。下列对有修改的类进行说明。

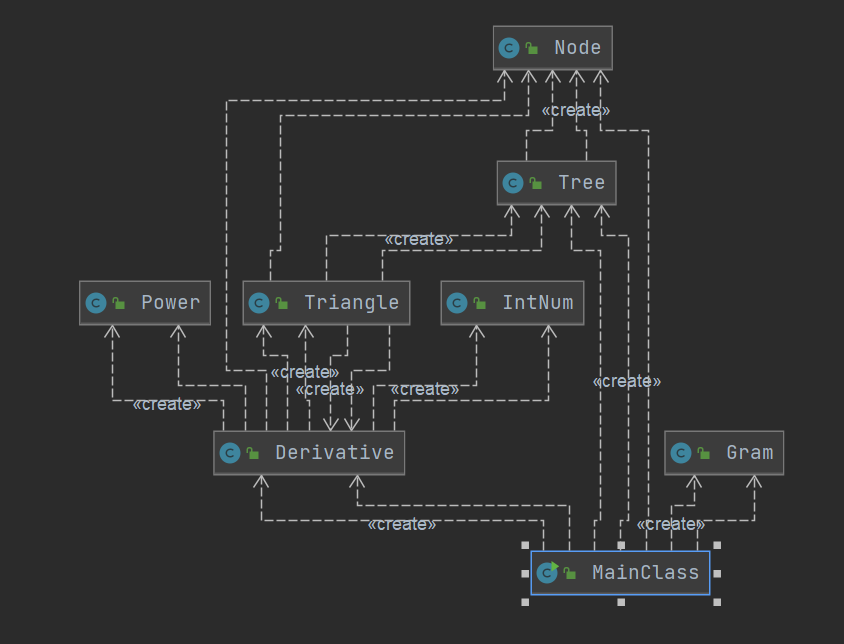
• MainClass
  与第二次作业相比，先通过字符串建立一个Gram类来验证形式，再通过建立语法树来求导。
  
• Triangle
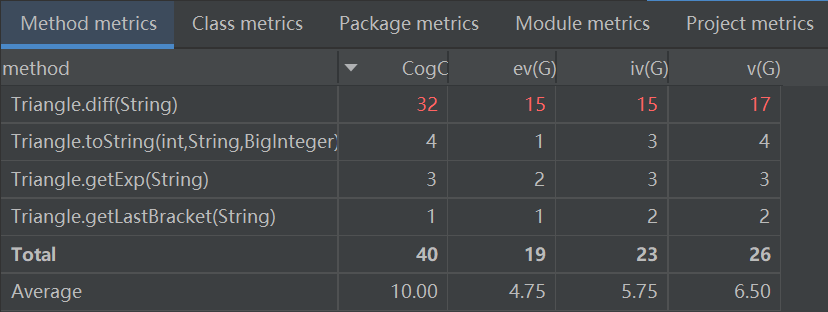
  新增方法getLastBracket来获取三角函数的最后一个‘*’的位置，新增了toString方法，对三角函数括号内的因子进行语法树构建以及求导，重写了diff方法，适合嵌套求导。
  
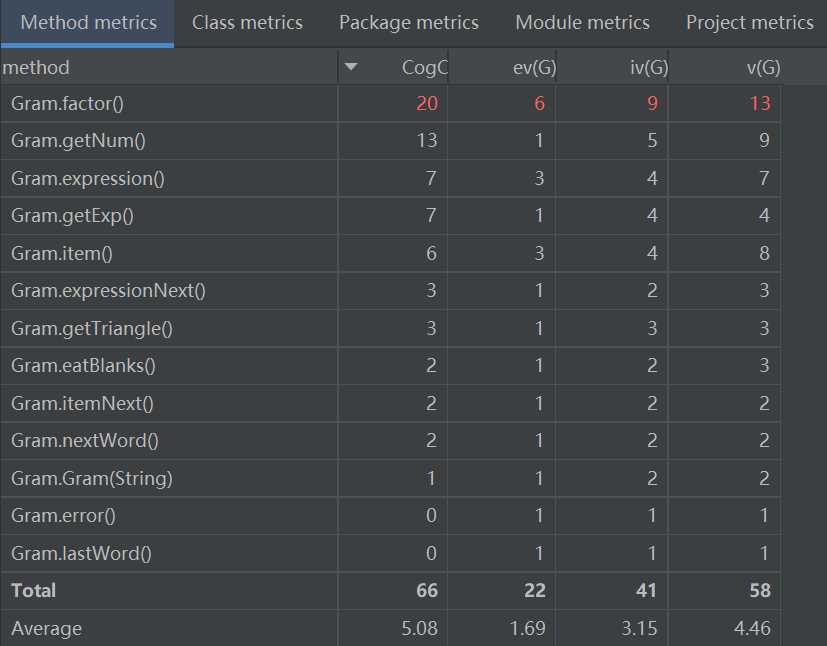
• Gram
  此类通过递归下降的方法来对表达式进行格式检查，具体规则参照形式性表述，遇错直接通过error方法退出程序。

优缺点分析

1. 优点
   • 将格式检查分离成单独一个类，体现了面向对象的思想。
2. 缺点
   • 格式检查之后再进行树的建立，这一步会多进行一次表达式的遍历，使得时间复杂度提高。

二、程序Bug分析

第一次作业

第一次作业的bug主要有以下两个方面：

1. 在字符串预处理的时候，画蛇添足的删去了前导0，但是正则表达式没有写正确，会导致删除*0+如此实际为0的数，或者会删除0之后的数。因此删去了前导0的替换工作，直接通过BigInteger的自带属性进行操作。
2. 对于最终表达式的输出，形式错误，因此将‘+-’之类的替换为相应的单个字符。
   以上两个bug都是细节问题，并没有对程序的实际性能造成多大影响，代码行数修改也在5行以内。

第二次作业

第二次作业我的是无效作业，究其原因bug实际上就是一种：
在提取到分离项的‘-’时，将‘-’提取为节点的data变量后，要将需要提取的右节点变号，并加上括号，这样才能防止符号错误。在提交样例中，思维混乱，想法是：利用之前的findAddOrSub方法找出减号的位置，再将分割后的字符串进行变号处理。这样写，方法的依赖性增强，再加上面向过程的思想，只能一个个特判，细节实现并不轻松，所以修改了很久的bug。修改时，独立写了一个changeSign方法，利用递归将一个字符串进行反复切割变号，很轻松就能解决这个问题。
这个bug是具体的实现问题，对于changeSign方法，它也反复调用了findAddOrSub方法，对圈复杂度影响集中在findAddOrSub上。
代码行数增加并不多，只有14行。

第三次作业

第三次作业的bug主要集中在格式检查上。由于对递归下降的理解并不深刻，没有牢牢地抓组形式性表达，因此只能在Gram类中进行特判，但许许多多特判是无止境的，说明从根本上这个结构就存在问题。在弱测和中测中始终有两个地方卡着。于是我按照形式化表述重新写了一遍，严格遵守它的规则，就能通过。
还有一个小bug，是细节问题，就是在嵌套函数求导时，使用的递归函数的条件有所欠缺，这里就不再阐述。
格式检查的bug思路没有问题，只是实现上的疏忽。

互测bug策略

在第一次作业中，我下载了几位同学的代码，看了一下大家的实现方法，然后综合了一些案例，进行构造数据互测，例如‘+-+’三个加减符号等等。但实际上，看代码是一个比较痛苦的过程，每个同学的思路不一样，在代码层次上的实现也不尽相同，代码风格更是参差不齐，读代码是一个非常耗时耗力的过程。读完代码之后，找到其中的bug也需要花费时间。第二次作业我并没有进入互测。第三次作业，就直接放弃了互测。

三、重构经历总结

我在写第二次作业的时候进行了重构。当我发现第一次作业的功能极为有限，并且后续功能还会继续增强的时候，就选择了重构。重构的方式选择很重要，需要提前想好构造思路，并且有可能的话还要思考除此之外还能增加什么功能，使程序的可拓展性增强。重构的基础，就是要把所需的结构理解透彻。第二次作业时候，考虑过语法树和递归下降，可递归下降是对我来说非常陌生的概念，而语法树在数据结构中曾学习过，因此我选择了语法树。还有一点非常重要，如果选择了重构，就一定要尽早开始，重构过程中会遇到大大小小的实现问题，需要查阅大量资料和修复大量bug，是需要很多时间的。

四、心得体会

第一单元对于我来说是无比艰难的。由于寒假的时间规划不合理，我的OO预习作业基本上没有完成，就直接进入了第一次作业。第一次作业的完成时的情况仿佛就在眼前：不会输出，不会调试，不懂得类与类之间的调用关系……诸多问题等待解决。仅仅是最简单的第一次作业，就让我感受到了无比沉重的压力。不过还好，感谢同学和助教的解答，让我强行上手了java。
这一单元最为痛苦的点就是第二次作业算为无效作业。那个星期，知道自己需要重构，但是对于递归下降这种方法一点也不熟悉，在网络上的资料也很难理清思路，因此迟迟没有动笔。直到周六中午，在讨论区发现了同学的语法树方法，结合了自己的能力，决定使用语法树。但时间已经很紧迫了，代码的具体实现总是会带来各种各样的问题，这种情况下，人的思路已经不清晰了，坐在电脑前也只是干坐着，好比一座僵尸，脑子早就不动了，只剩下焦虑。记得在周日晚九点40左右提交之后，发现还是没过，心已经凉了，虽然又发现自己的bug在哪了，但也是无济于事，因为在这种情况下你根本改不对。之后的两天，我没有看过OO。星期二晚上再次看起OO时，仅仅坐了一个小时，就把之前的方法全部重新修改并且正确提交了，心里滋味蛮复杂的，有可惜，但是明白了OO这门课一定要早点去思考，不能拖延。
第三次作业的时候，就吸取了上次的教训，很早就开始思考递归下降的写法了。看着博客，以及从其他同学那里找的互测房中使用递归下降写法的同学的代码，最终还是摸索出了一点皮毛。
因此，OO这门课需要查找的资料很多，需要提早学习，充足预习，要留出足够的时间思考，并且尽早动笔来具体实现。希望在吸取了第一单元的惨痛教训后，我能继续在OO上激流勇进。