网络流最小割，无向图建图法，求最小割点转换求最小割边

洛谷P1345

假设原来的点编号为i，总共有n个点，那么我们就把每个点拆成两个点，编号分别为i和i+n。其中点i负责连接原图中连入这个点的边，点i+n负责连原图中连出这个点的边。

add ( i, i+n, 1 ) ; 
add ( i+n, i, 0 ) ;

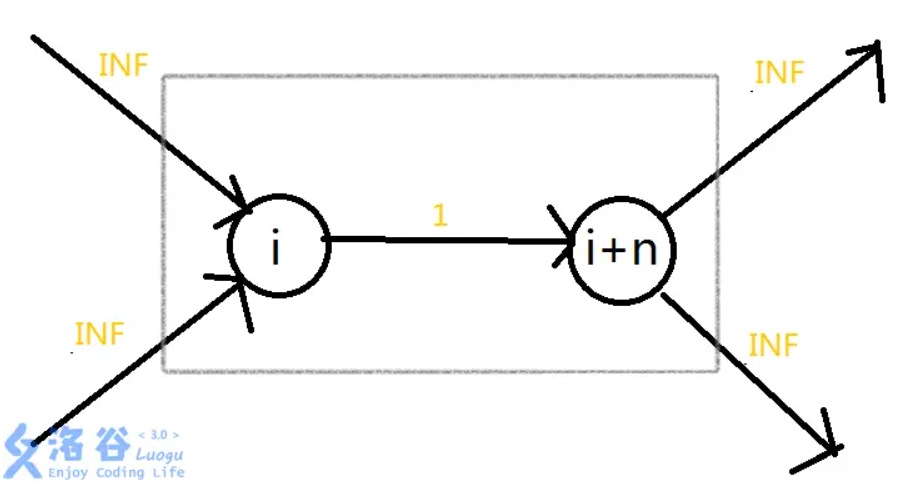
对于原图中本来就存在的边，它们只是有一个联通的作用，对于流量并没有限制，所以明确一点：这些边加入网络中限制应该为无限大。
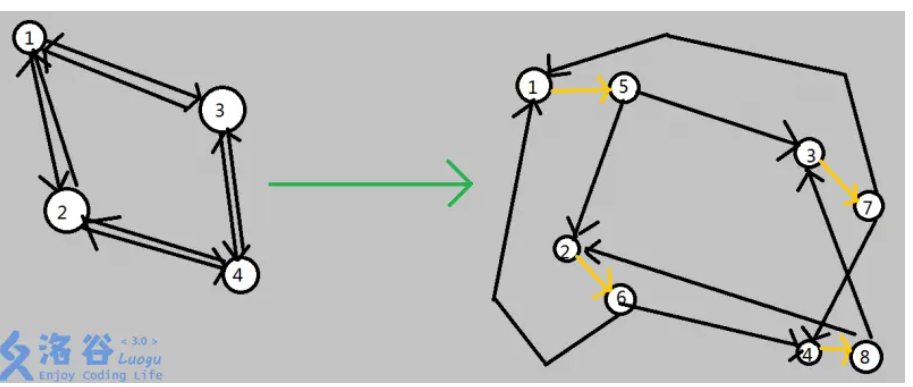
假设现在要从原图中添加一条从x到y的有向边（这道题是无向边，再依下面的方法添加一个y到x的就行了）到网络中去，对于点y来说，这条边的加入不应该影响通过它的流量限制（就是前面连的那个1）发生变化，所以前面那条y到y+n的边应该接在这条边的后面，所以这条边的终点连向网络中的y，相反的，这条边应该受到x的（前面连的1）限制。因为，假设x已经被删（x到x+n满流），那么这条边再加不加都是没有变化的。所以，这条边在网络中的起点应该是x+n，这样才保证受到限制。

add ( y+n, x, 无限大 ) ;
add ( x, y+n, 0 ) ;
add ( x+n, y, 无限大 ) ;
add ( y, x+n, 0 ) ;

code:

#include<bits/stdc++.h>
using namespace std;
const int N=210,M=(600<<2)+(N<<1),INF=0x3f3f3f3f;
struct edge{int v,c,ne;}e[M];
int h[N],cur[N],d[N],id=1;
int n,m,s,t;
void add(int u,int v,int c){
    e[++id]={v,c,h[u]};
    h[u]=id;
}
bool bfs(){
    memset(d,0,sizeof(d));
    queue<int> q;
    q.push(s);
    d[s]=1;
    while(q.size()){
        int u=q.front();
        q.pop();
        for(int i=h[u];i;i=e[i].ne){
            int v=e[i].v;
            if(d[v]==0&&e[i].c){
                d[v]=d[u]+1;
                q.push(v);
                if(v==t)
                    return true;
            }
        }
    }
    return false;
}

int dfs(int u,int mf){
    if(u==t)
        return mf;
    int sum=0;
    for(int i=cur[u];i;i=e[i].ne){
        int v=e[i].v;
        cur[u]=i;
        if(d[v]==d[u]+1&&e[i].c){
            int  f=dfs(v,min(mf,e[i].c));
            mf-=f;
            sum+=f;
            e[i].c-=f;
            e[i^1].c+=f;
            if(mf==0)
                break;
        }
    }
    if(sum==0)
        d[u]=0;
    return sum;
}
int dinic(){
    int flow=0;
    while(bfs()){
        memcpy(cur,h,sizeof(h));
        flow+=dfs(s,INF);
    }
    return flow;
}
int main(){
    cin.tie(nullptr)->sync_with_stdio(false);
    cin>>n>>m>>s>>t;
    add(s,s+n,INF);
    add(s+n,s,0);
    add(t,t+n,INF);
    add(t+n,t,0);
    for(int i=1;i<=n;i++){
        if(i==s||i==t)
            continue;
        add(i,i+n,1);
        add(i+n,i,0);
    }
    t=t+n;
    for(int i=1;i<=m;i++){
        int u,v;
        cin>>u>>v;
        add(u+n,v,INF);
        add(v,u+n,0);
        add(v+n,u,INF);
        add(u,v+n,0);
    }
    cout<<dinic()<<endl;
    return 0;
}