P9914 题解

这题在赛场是卡了我好久。

思路

首先，这些人是可以在非整数时间相遇的。

拿样例来说：

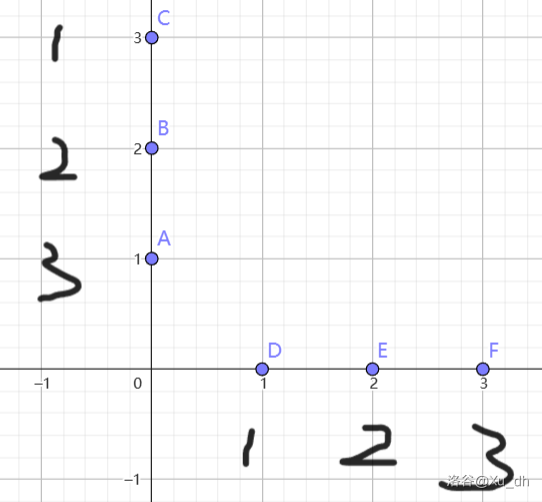
数字是速度，字母是我命名的编号。

为什么点 \(D\) 不能和点 \(A\) 在 \((1,1)\) 相遇呢。
因为他们到达的时间不一样。

而点 \(E\) 和点 \(B\) 能在 \((2,2)\) 相遇因为他们到达那里的时间一样。

由此可以得出暴力代码。

#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000005],b[1000005];
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int j=1;j<=m;j++){
		cin>>b[j];
	}
	long long ans=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(a[i]!=0&&b[j]!=0&&1.0*i/b[j]==1.0*j/a[i])ans++;
		}
	}
	cout<<ans;
	return 0;
}

如果两个点到达某个点时间一样，那么它们可以相遇。如下面这样的式子。

\[i \div b_j = j \div a_i \]

既然只要判断是否相等，那就用 unordered_map。

unordered_map 是 map 的变种，可以统计个数，但是不保证有序。

为了方便所以给式子移项。得到的式子如下。

\[i \times a_i = j \times b_j \]

接下来只需要将 \(i \times a_i\) 丢进 unordered_map 里面计数，再看看里面有多少个 \(b_j \times j\)，加上就好了。

注意 \(i \times a_i\) 时 \(a_i\) 是否等于 \(0\) 无所谓，但是 \(j \times b_j\) 时 \(b_j\) 必须不等于 \(0\)。

AC CODE

#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,m,a[1000005],b[1000005],ans;
unordered_map<int,int>mp;
signed main(){
	ios::sync_with_stdio(0);
	cin.tie(0),cout.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		cin>>a[i];
	}
	for(int j=1;j<=m;j++){
		cin>>b[j];
	}
	for(int i=1;i<=n;i++){
		if(a[i]!=0)mp[a[i]*i]++;
	}
	for(int j=1;j<=m;j++){
		if(b[j]!=0)ans+=mp[b[j]*j];
	}
	cout<<ans;
	return 0;
}