【Leetcode】84. 柱状图中最大的矩形

 

 

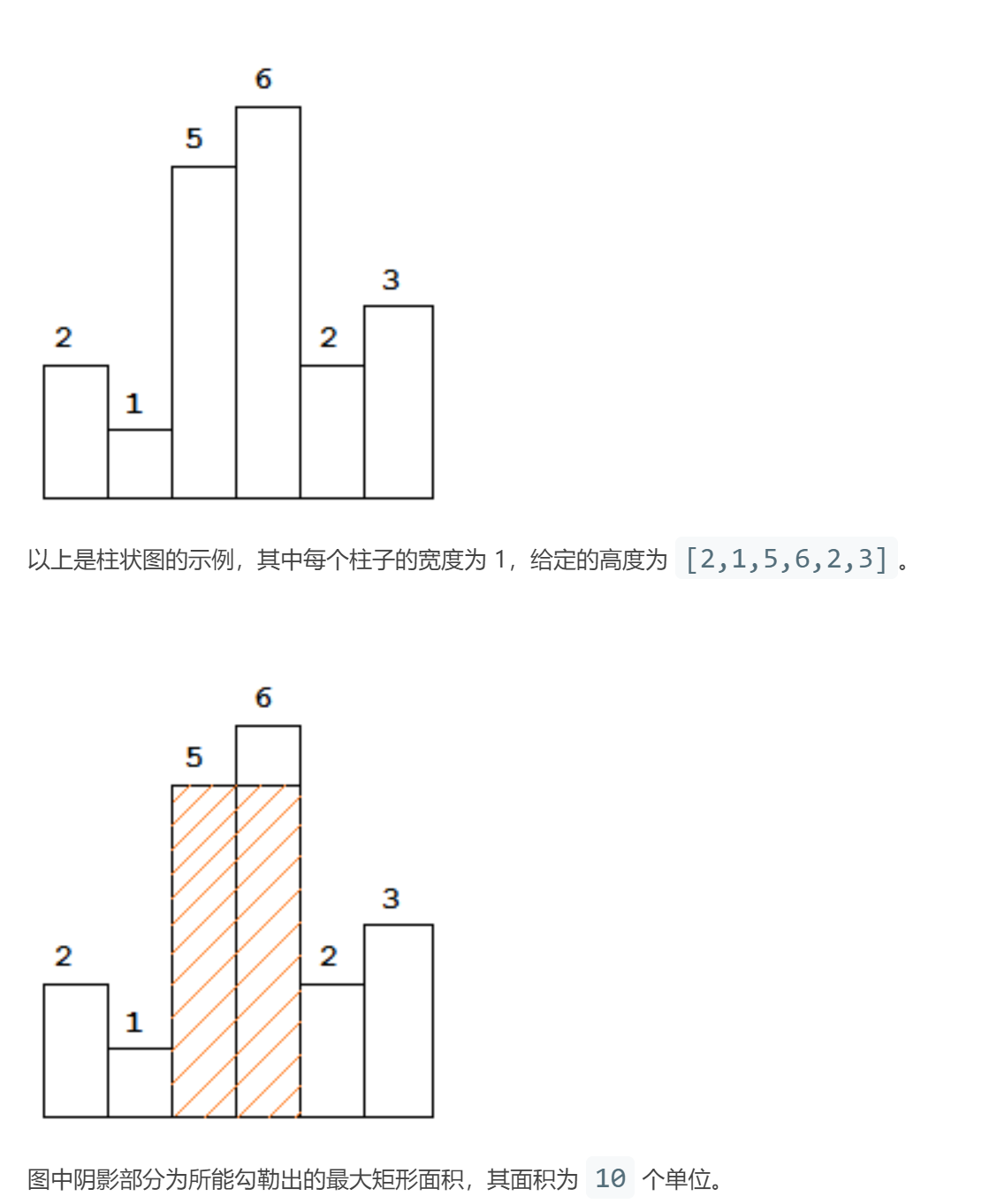
 暴力解法一：枚举宽度

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int ans = 0;
        // 枚举左边界
        for (int left = 0; left < n; ++left) {
            int minHeight = Integer.MAX_VALUE;
            // 枚举右边界
            for (int right = left; right < n; ++right) {
                // 确定高度
                minHeight = Math.min(minHeight, heights[right]);
                // 计算面积
                ans = Math.max(ans, (right - left + 1) * minHeight);
            }
        }
        return ans;
    }
}

暴力解法二：枚举高度

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        int ans = 0;
        for(int mid = 0; mid < n; mid++){
            int left = mid;
            int right = mid;
            int height = heights[mid];
            while(left-1 >= 0 && heights[left-1] >= height){
                left--;
            }
            while(right+1 < n && heights[right+1] >= height){
                right++;
            }
            ans = Math.max((right-left+1)*height,ans);
        }
        return ans;
    }
}

枚举高度的思路和单调栈结构是一样的，找到当前数字左右两边距离最近的比它小的值的位置。

单调栈的实现思路：始终保持一个栈的单调性，如果入栈元素A试图破坏单调性，栈顶元素X出栈，

我们可以获得X的两边小值的信息，让X出栈的入栈元素A就是X右边最近的小值，X出栈之后的栈顶元素B就是X左边最近的小值。

如果X弹出后入栈元素A还是破坏单调性，则继续弹出，重复上述过程；

如果不破坏单调性，A入栈。

遍历完数组之后，栈不空，依次弹出栈，且这些元素的右边没有比它小的值，左边比它小的值是弹出后的栈顶元素。

这道题是找左右两边较小的值，所以从栈顶到栈底是单调递减的

如果是找左右边较大的值，栈顶到栈底就该是单调递增的。

 

使用单调栈来解：

在单调栈中，如果左边和右边有没有比当前值小的返回（-1，-1）

在这里使用单调栈的关键就是弄清楚没有找到较小值的时候left和right的值怎么设置

当左边没有较小值的时候，说明从cur位置可以一直延申到0位置

当右边没有较小值的时候，说明从cur位置可以一直延申到数组末尾位置

class Solution {
    public int largestRectangleArea(int[] heights) {
        int n = heights.length;
        Stack<Integer> stack = new Stack<>();
        int ans = 0;
        //栈顶元素较大
        for(int i = 0; i < n; i++){
            while(!stack.isEmpty() && heights[stack.peek()]>heights[i]){
                int cur = stack.pop();
                int right = i;
                int left = stack.isEmpty()?-1:stack.peek();
                System.out.println(left+" "+cur+" "+right);
                ans = Math.max(ans, (right-left-1)*heights[cur]);
            }
            stack.push(i);
        }
        while(!stack.isEmpty()){
            int cur = stack.pop();
            int right = heights.length;
            int left = stack.isEmpty()?-1:stack.peek();
            System.out.println(left+" "+cur+" "+right);
            if(right == cur && left == -1){
                ans = Math.max(ans, heights[cur]);
            }
            ans = Math.max(ans, (right-left-1)*heights[cur]);
        }
        return ans;
    }
}