基础树形DP

曾经的黑历史(

有空了重构一下

模板

P1352 没有上司的舞会

树状\(dp\)模板题。

设\(f[i][0]\)为第\(i\)个人来了的方案数

\(f[i][1]\)为第\(i\)和人没来的方案数

若第\(i\)个人来了,那么其下属均不回来

若不来,其下属则有来和不来两种选择

因此状态转移方程为:

\(f[i][0]+=f[son][1]\)
\(f[i][1]+=max(f[son][0],f[son][1])\)

P2015 二叉苹果树

树上背包模板题

每一个枝条都有"剪"和"不剪"两种可能

把每一个儿子都看成一个"分组背包"

设\(dp[i][j]\)表示第\(i\)个子树保留\(j\)条边

每加入一个"儿子"后,枚举该"儿子"保留的边数,如图

(ps:这里i-k后面还要减1是因为还要多保留从u->v这条边)

故状态转移方程为:

\(f[u][i]=max(f[v][i-k-1]+f[u][k]+w[u][v])(i\in[1,m+1)]\)

树上背包

P2014 [CTSC1997]选课

P1273 有线电视网

P1270 “访问”美术馆

P1272 重建道路

P2014 [CTSC1997]选课

和二叉苹果树一样的套路。

把每一个子课程都看作是一个"分组背包",倒序枚举即可

由于题目中可能有多棵树

因此多开一个节点把所有"树根"连在一起

同时,在倒序枚举时也要把这个新节点算进去

转移方程:

\(f[u][i]=max(f[v][i-k-1]+f[u][k]+w[v])(i\in[1,m+1])\)

核心代码:

void dp(int k){
	vis[k]=1;
	for(int i=0;i<son[k].size();i++){
		if(vis[son[k][i]]!=1){
			dp(son[k][i]);
			for(int v=m+1;v>=1;v--){
				for(int K=0;K<v;K++){
					 f[k][v]=max(f[k][v],w[son[k][i]]+f[son[k][i]][K]+f[k][v-K-1]);
				}
			}
		}
	}
	return;
}

P1273 有线电视网

也是比较经典的一个树上背包问题

题目中要求的是在不亏本的情况下最多的观看用户个数

设\(f[i][j]\)表示第\(i\)个站传输给\(j\)个用户观看最终剩余的钱数

若最终剩余钱数大于等于0,则说明未亏本

反之,则说明亏本

转移方程则为:

\(f[u][i]=max(f[v][k]+f[u][i-k]-w[u][v])\)

\(dp\)完后从总人数开始倒序判断是否亏本即可

贴个核心代码:

\(dp部分\)

void dfs(int x){
	dp[x][0]=0;
	if(val[x]){//如果是根节点
		size[x]=1;//人数加一
		dp[x][1]=val[x];
		return;
	}
	for(int i=0;i<son[x].size();i++){
		dfs(son[x][i]);
		size[x]+=size[son[x][i]];//计算x节点下的人数总和
		for(int j=size[x];j>=0;j--){//滚动数组,倒序枚举
			for(int k=1;k<=size[son[x][i]];k++){//枚举子树传输的观众数量
				dp[x][j]=max(dp[x][j],dp[x][j-k]+dp[son[x][i]][k]-W[x][son[x][i]]);
			}
		}
	}
	return;
}

\(判断部分\)

     for(int i=m;i>=0;i--){
	if(dp[1][i]>=0){//如果不亏本
	cout<<i;
	break;
	}
}

P1270 “访问”美术馆

跟P1273 有线电视网一样的套路

设\(f[i][j]\)为在第\(i\)个节点下偷\(j\)幅画所需要的最小总时间

状态转移方程也就呼之欲出了

\(f[u][i]=min(f[v][k]+f[u][i-k]-2w[u][v])\)

这里\(w[u][v]\)要乘2是因为要进出各一趟

核心代码:

int dfs(int x){
	if(paint[x]!=0){
		return paint[x];
	}
	int s=0;
	for(int i=0;i<son[x].size();i++){
		
		int v = son[x][i];
		int t=dfs(v);
		s+=t;
		for(int j =s;j>0;j--){
			for(int k=0;k<=t;k++){
				dp[x][j] = min(dp[x][j] , dp[v][k] + dp[x][j-k]+w[x][v]*2);
			}
		}
	}
	return s;
}

P1272 重建道路

同样也是一道比较经典的树上背包问题

设\(f[i][j]\)为第\(i\)个节点断出一个大小为\(j\)的子树所需要的断开总数

状态转移方程:

\(f[u][i]=min(f[v][k]+f[u][i-k]-1)\)

(\(v\)为根的子树提供\(k\)个节点,\(u\)和其他儿子提供\(j-k\)个节点)

同时,由于一开始时一个子树都没有加进来

即把\(u\)的所有"儿子"都切断了

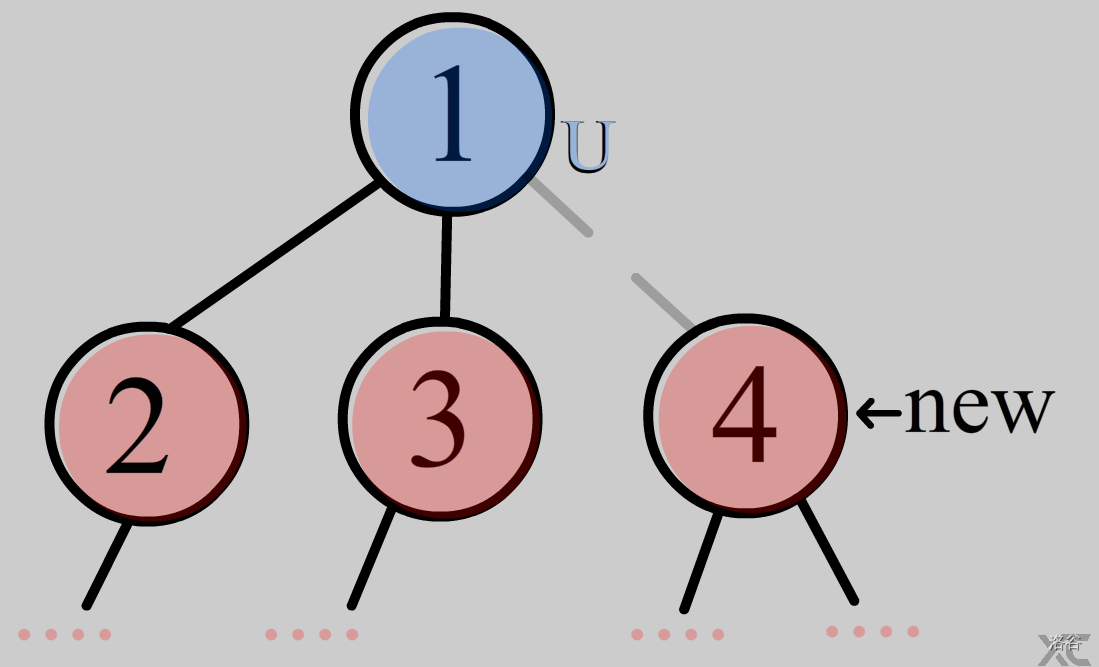
因此当把\(v\)儿子加进来的时候要把之前那段减去的边加回来

核心代码:

void dfs(int x){
	size[x] = 1;
	if(!is_son[x]){
		dp[x][1] = 0;
		size[x] = 1;
		return;
	}
	for(int i=0;i<son[x].size();i++){
		int v = son[x][i];
		dfs(v);
		size[x]+=size[v];
		for(int j = size[x];j>=0;j--){
			for(int k = 1;k<=size[v];k++){//这里题解里很多人都写成了<j,问题是子树可能本身就没有这么多子节点,感觉有些问题
				dp[x][j] = min(dp[x][j],dp[x][j-k]+dp[v][k]-1);
			}
		}
	}
}

普通树形\(DP\)

P2016 战略游戏

P2458 [SDOI2006]保安站岗题解

P4084 [USACO17DEC]Barn Painting G

P2585 [ZJOI] 三色二叉树

P2279 消防局的设立

P2016 战略游戏

带了点贪心思想的树形\(DP\)

如果父节点放了一个守卫

那其子节点就都不用放守卫了

反之,子节点都要放一个守卫

转移方程:

\(f[u][0]+=f[v][1]\)
\(f[u][1]+=min(f[v][1],f[v][0])\)

为什么不用儿子的儿子("孙子")节点来看守儿子节点?

如果一个节点不是叶子节点,那他的子节点数必定大于或等于\(1\),因此如果用儿子节点来看守其父节点,花费的数量肯定会更多(或不变)。

遗憾的是题解里似乎没人说正确性的证明?,还是说太简单了都懒得证了

核心代码:

void dfs(int x){
   if(x!=1509)
	dp[x][1]=1,dp[x][0]=0;
	for(int i=0;i<son[x].size();i++){
		dfs(son[x][i]);
		dp[x][0]+=dp[son[x][i]][1];
		dp[x][1]+=min(dp[son[x][i]][1],dp[son[x][i]][0]);		
	}
}

关于这道题目的带点权版:

P2458 [SDOI2006]保安站岗

题解链接

P4084 [USACO17DEC]Barn Painting G

树上\(DP\)求方案数。

还算是比较简单的题目吧...

设:

\(f[i][0]\)为第\(i\)个节点涂红色的方案数

\(f[i][1]\)为第\(i\)个节点涂绿色的方案数

\(f[i][2]\)为第\(i\)个节点涂蓝色的方案数

假设第\(i\)号节点涂了红色,那么它的上一个节点就只能涂绿色和蓝色

其他情况也同理

用乘法定理乘一下即可。

转移方程:

\(\begin{cases}f[u][1]=f[u][1]*((f[v][2]+f[v][3]))\\f[u][2]=f[u][2]*((f[v][1]+f[v][3]))\\f[u][3]=f[u][3]*((f[v][1]+f[v][2]))\end{cases}\)

换根\(DP\)

一种形式十分优美的树形\(DP\)

P3478 [POI2008]STA-Station

P2986 [USACO10MAR]Great Cow Gathering G

P3047 [Nearby Cows G]Great Cow Gathering G

CF708C Centroids

CF1187E Tree Painting

P3478 [POI2008]STA-Station

换根DP的模板题。

这里我们设

\(size[i]\)为以\(1\)为根节点时节点\(i\)的子树大小
\(dep[i]\)为以\(1\)为根节点时节点\(i\)的深度大小
\(dp[i]\)为以\(i\)为根节点时深度之和的大小

很明显,我们可以通过一遍DFS求出以\(1\)为根节点时的深度之和

如果一个个的去算的话

照这个数据范围,显然会T飞

这个时候就要用到换根DP了

换根\(DP\)优化

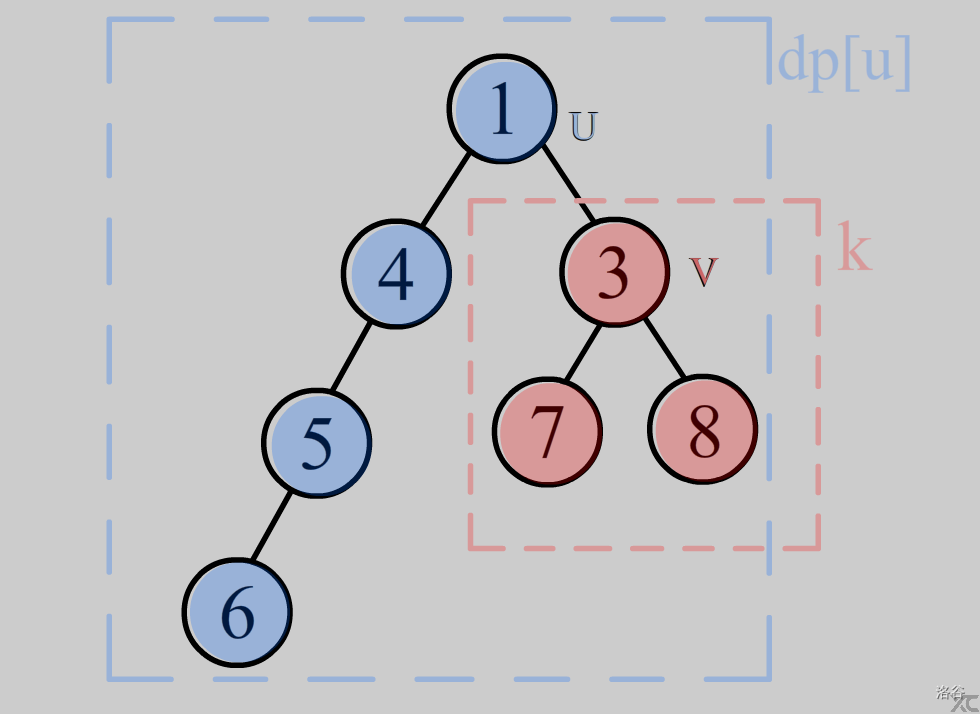
可以看出,当我们把根节点从1换到3时

对子节点3的贡献由两部分组成

1.自己子树的贡献(图中的k)

2.父亲节点\(1\)的贡献

如何转移

首先是\(k\),作为自己子树所产生的贡献肯定要加上
\(dp[u]\)为以\(u\)为根节点时的深度总值,在计算时,要减去\(v\)的子树所产生的贡献,不然就重复计算了,同时

在以 \(u\)为根时,v节点及其子树内的所有节点的深度都增加了\(1\),需要减去

(图中红色的节点)

合起来就是\(dp[u]-(size[v]+k)\)

除v子树外的其他节点也一样

在以\(v\)为根时，除\(v\)节点及其子树外的其他节点的深度都增加了\(1\)

(图中蓝色的节点)

合起来就是\((size[1]-size[v])\)

得到转移方程

\(dp[v] = k+(dp[u]-(k+size[v]))+(size[1]-size[v])\)

化简一下

\(dp[v] = dp[u]-2size[v]+size[1]\)

核心代码:

void dfs1(int x){
	size[x] = 1;
    vis[x] = 1;
	for(int i=0;i<son[x].size();i++){
		int v = son[x][i];
		if(!vis[v]){
		dep[v] = dep[x] +1;
		dfs1(v);
		size[x]+=size[v];	
		}
			
	}
}
void dfs2(int x){
    vis[x] = 1;
	for(int i=0;i<son[x].size();i++){
		int v = son[x][i];
		if(!vis[v]){
		dp[v] = dp[x] +size[1] - 2*size[v];
		dfs2(v);	
		}
	}
}

P2986 [USACO10MAR]Great Cow Gathering G

前面那道题目的带权值版

一模一样的思路,只需要把状态转移方程转换一下即可。

 void dfs(int u,int fa){
	
	
    for(int i=head[u];i;i=edge[i].next){
    	int v =edge[i].v;
    	if(v==fa) continue;
    	dfs(v,u);
    	size[u] += size[v];
    	sum[u]+=(sum[v]+edge[i].w*size[v]);	
	}
}

 void dp(int u,int fa){
	for(int i=head[u];i;i=edge[i].next){
    	   int v =edge[i].v;
			   	if(v==fa) continue;
			f[v] = 1LL*f[u] + AN*edge[i].w - 2*size[v]*edge[i].w;
			ans = min(ans,f[v]);
			dp(v,u);
	}
}

P3047 [Nearby Cows G]

1.\(状态表示\)

设\(size[i][j]\)为第i个节点向下\(j\)层所包含的点权和

\(f[i][j]\)为第\(i\)个点距离它不超过 \(j\)的所有节点权值和

2.状态转移

对于\(size[i][j]:\)

\(size[u][j] =\sum\ size[v][j-1]\) 自己向下\(j\)层即为儿子向下\(j-1\)

对于\(f[i][j]:\)

儿子对它的贡献:

\(size[v][j]\)

自己向下\(j\)层,儿子节点肯定也要向下\(j\)层

父亲对它的贡献:

\(f[u][j-1]-size[v][j-2]\)

父亲节点扩展\(j-1\)层的值减去和儿子节点的值所重复包含的\(j-2\)层值

转移方程:

\(f[v][j] = f[u][j-1]+size[v][j]-size[v][j-2]\)

核心代码:

void dfs(int u,int fa){
	
	for(int i=head[u];i;i=edge[i].next){
		int v =edge[i].v;
		if(v==fa) continue;
		dep[v]=dep[u]+1;
		dfs(v,u);
		for(int i=1;i<=k;i++){
			size[u][i]+=size[v][i-1];
		}
	}
}
void dp(int u,int fa){
	
	for(int i=head[u];i;i=edge[i].next){
		int v=edge[i].v;
		if(v==fa) continue;

		for(int i=1;i<=k;i++){
			if(i-2>=0)
			f[v][i] = size[v][i]+f[u][i-1] - size[v][i-2];
			else f[v][i] = size[v][i]+f[u][i-1];
		}
			
		dp(v,u);
	}
}

CF708C Centroids

一道做起来比较麻烦的换根\(DP\)

分析

首先对于一个节点来说,大小大于\(n/2\)的节点肯定只有一个，这个显而易见

再来看如何改造

如果说该节点本身的重儿子就小于\(n/2\),那肯定可以成为树的重心

反之,肯定要在重儿子里找出一个重量最大的且小于等于\(n/2\)的子树,并将其断开,连接到根节点上(相当于删去这颗子树)

如果重儿子的大小减去被删去儿子的大小小于等于\(n/2\),则说明可以改造

反之,无法改造

如何转移

分两种情况来讨论

\(1\).该节点不是其父亲节点重儿子

其父节点的重儿子不会被改变,只需要判断该节点的重儿子是否改成其父节点即可

\(2\).该节点是其父亲节点的重儿子

其父亲节点的重儿子会变为其"次大"儿子,其儿子节点的重儿子不会改变

核心代码：

void dfs(int u){
	vis[u] = 1;
	size[u] = 1;
	for(int i=0;i<son[u].size();i++){
		int v = son[u][i];
		if(!vis[v]){
		dfs(v);
		size[u]+=size[v];
		if(size[v] > size[maxson[u]])
			maxson[u] = v;	
	  }	
	 }
	   
			if(maxson[u]!=0){
				
				if(size[maxson[u]]<=n/2) dp[u] = size[maxson[u]]; 
				else dp[u] = dp[maxson[u]];
			}
}


void exchange(int u,int v){
        size[u] = size[u] - size[v];
		size[v] = size[v] + size[u];
		if(v==maxson[u]){
			maxson[u] = 0;
			for(int i=0;i<son[u].size();i++){
				int V = son[u][i];
				if(V!=v&&size[V] > size[maxson[u]]){
					maxson[u] = V;
				} 
			}
			if(maxson[u]!=0){
				
				if(size[maxson[u]]<=n/2) dp[u] = size[maxson[u]];
				else dp[u] = dp[maxson[u]];
			}
		}
		if(size[maxson[v]]<size[u]){
			maxson[v] = u;
			if(maxson[v]!=0){
				
				if(size[maxson[v]]<=n/2) dp[v] = size[maxson[v]];
				else dp[v] = dp[maxson[v]];
			}
		}	
}
void dfs2(int u){
	vis[u]  = 1;
    
	 if(size[maxson[u]]<=n/2||size[maxson[u]] - dp[maxson[u]]<=n/2) ans[u]=1;
	for(int i=0;i<son[u].size();i++){
		int v = son[u][i];
		if(!vis[v]){
			exchange(u,v);
			dfs2(v);
			exchange(v,u);
		}
	}
}

end.

基环树部分还是先缓缓吧,暂时还未完全掌握

posted @ 2020-08-02 21:15 xcxc82 阅读(178) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

xcxc82

基础树形DP

模板

P1352 没有上司的舞会

P2015 二叉苹果树

(ps:这里i-k后面还要减1是因为还要多保留从u->v这条边)

树上背包

P2014 [CTSC1997]选课

P1273 有线电视网

P1270 “访问”美术馆

P1272 重建道路

普通树形\(DP\)

P2016 战略游戏

遗憾的是题解里似乎没人说正确性的证明?,还是说太简单了都懒得证了

P2458 [SDOI2006]保安站岗

题解链接

P4084 [USACO17DEC]Barn Painting G

换根\(DP\)

P3478 [POI2008]STA-Station

换根\(DP\)优化

如何转移

P2986 [USACO10MAR]Great Cow Gathering G

P3047 [Nearby Cows G]

1.\(状态表示\)

2.状态转移

CF708C Centroids

分析

如何转移

公告