一阶Lipschitz连续性对GAN的帮助

若\(x\)属于有界空间\(\mathbb{R}^n\)，则定义在实数域上的函数\(f(x)\)有界的充分条件是函数\(f\)满足Lipschitz（一般指的是一阶的）连续性。
但却不是必要条件，因为反过来论述是不对的。

证明非常简单：
充分性是成立的
若函数\(f\)满足Lipschitz连续性，则必定满足，对任意\(a, b \in \mathbb{R}^n\), 存在常数K满足

\[|f(b) - f(a)| \leq K\cdot|b-a| \]

接下来，先证明\(f(x)\)中必定存在一个非无穷大值\(f(x_0)\)。
采用反证法：
若\(f(x)\)中所有值都是无穷大，那么对任意\(a, b \in \mathbb{R}^n\)，都有\(|f(b) - f(a)| = +\infty\) .
然而，由于\(\mathbb{R}^n\)是有界的，因此必定存在非无穷大值常数\(C\)满足\(|b-a|\leq C, C\geq 0\)，
那么，必然可得：

\[|f(b) - f(a)| = +\infty > K\cdot C \geq K\cdot |b-a| \]

该结论显然和Lipschitz连续性的假设冲突，因此，\(f(x)\)中不都是无穷大。
也即，至少存在一个非无穷大值\(f(x_0)\)。
回到主线，继续证明充分性：
假设\(f(x_0)\)是一个非无穷大值，对任意\(x\in \mathbb{R}^n\)，由于\(f(x)\)满足Lipschitz连续性，因此必然存在

\[|f(x) - f(x_0)| \leq K\cdot|x - x_0| \leq K\cdot C \]

从而，

\[K\cdot C - f(x_0) \leq f(x)\leq K\cdot C + f(x_0) \]

因此，\(f(x)\)是有界的，命题的充分性得证。

必要性是不成立的
当\(f(x)\)有界时，不存在常数\(K\)使得任意\(a, b\in\mathbb{R}^n\)满足\(|f(b)-f(a)|\leq K\cdot|b-a|\)。
换言之，对于任意给定的常数\(K\)，总能找到\(a, b\in\mathbb{R}^n\)使得\(|f(b)-f(a)|>K\cdot|b-a|\)。
可以举个非常特殊的例子，这个例子可以打破你的一切幻想（不管你设想的条件多么苛刻，这个例子都能满足，但却始终不满足Lipshitz连续性：

\[\begin{equation} f(x)=\left\{ \begin{aligned} \sqrt{x} & , & x >= 0 \\ -\sqrt{-x} & , & x < 0 \end{aligned} \right. \end{equation} \]

画出其曲线为下图

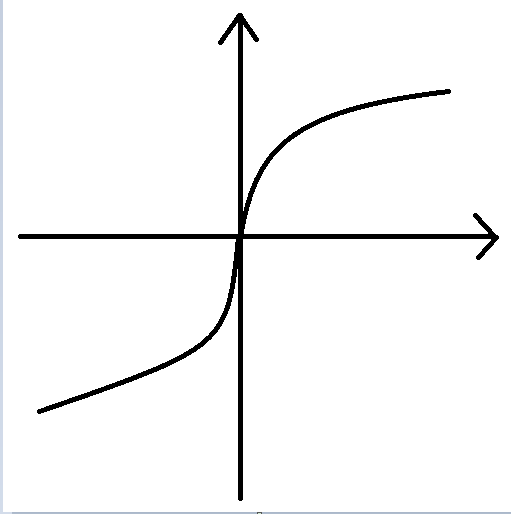
从图上来看\(f(x)\)在定义域上是连续的，但在\(x=0\)处不可微，对于该函数分段求一阶导数，发现此处的一阶微分是\(+\infty\)，
因此根据无穷大的定义，如果在\(x=0\)附近的邻域\(\Omega_{x=0}\)内取点，对于任意给定的\(K\)，我们总能找到\(a,b\in \Omega_{x=0}\)，
使得\(\frac{f(b)-f(a)}{b-a} > K\)，也即对任意给定的\(K\)，都能在0附近找到\(a, b\)，使得\(|f(b)-f(a)| > K\cdot|b-a|\)。显然必要性是不成立的。

在GAN的训练过程中，为了避免GAN发生模式崩溃，通常会采用梯度裁剪的方式来稳定GAN的训练过程，事实上，其他归一化手段也有类似的效果。
梯度裁剪中采用的是梯度L1归一化，起到的效果就是使得由梯度塑造的生成器模型(Generator)，在各点的局部具有Lipshitz连续性，
这种超出本愿（只想稳定GAN，约束输出的值域）的过强假设，将损害生成器模型的构造能力，（类似于限制一个人的思考组合空间，
而强行让一个人的思维具备连续性，违背了思维的可跳跃性的基本假设。）生成器生成的样本的多样性将大打折扣。