网络流小结

网络流小结

之前培训讲过的网络流一直没懂，经过一周的不懈努力，终于搞定了这个网络最大瘤，特此总结一下。

一. 定义

有向图 G = ( V , E ) 中：有唯一的源点 S（入度为 0，出发点），有唯一的汇点 T（出度为 0，结束点），图中每条弧（u , v）都有一个非负容量 c ( u , v )，满足上述条件的图 G 被称为网络流图 。

太抽象？给个图李姐李姐：

 

 

何为最大流？

简单来说就是水流从一个源点 s 通过很多路径，经过很多点，到达汇点 t，问你最多能有多少水能够到达 t 点 。 

例如上面的图的最大流就是 6+4+2=12

怎么求得呢？

或许你会有一个这样的思路：从 s 开始找所有能到达t的路径，然后找每条路径上权值最小的边（或者说能承受水流最小的管子），再进行其它操作，就能找到这张图的最大流。

于是我们就有了 EK（Edmond—Karp）算法

二. EK算法

引入一个概念：

增广路：增广路是指从s到t的一条路，流过这条路，使得当前的流（可以到达t的人）可以增加。

那么我们求最大流的问题，就是转化为不断求增广路的问题，这就是 EK 算法的核心思想！

那怎么做呢？

其实很简单，直接从 s到 t 广搜即可，从 s 开始不断向外广搜，通过权值大于 0 的边（因为后面会减边权值，所以可能存在边权为 0 的边），直到找到 t 为止，然后找到该路径上边权最小的边，记为 flow，然后最大流加 flow，然后把该路径上的每一条边的边权减去 flow，直到找不到一条增广路（从 s 到 t 的一条路径）为止。 

还是以图为例啦：

 

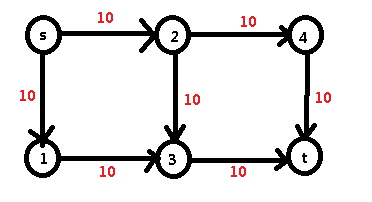
假如我们先走 s -> 2 -> 3 -> t，找到的增广路的大小为 10（路径上的最小容量），路径每个边减 10，然后答案加 10：

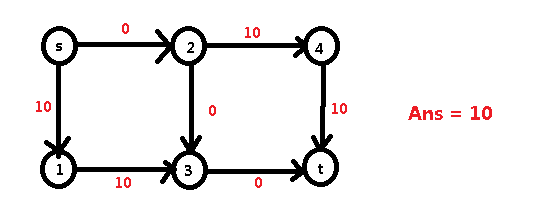
然后我们发现我们找不到其余的增广路了，那么最后的答案就是 10 嘛？

当然不是啊，明显有更优的走法嘛：

假如我们先走 s -> 2 -> 4 -> t ：

 

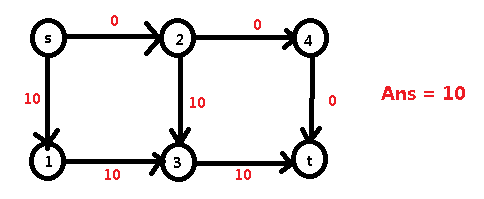
然后我们还可以继续走 s -> 1 -> 3 -> t ：

 

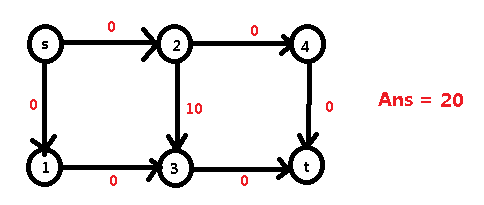
通过这样的走法，我们得到了真正的答案 20 ！ 

但是问题来了：程序知道要这么走？

显然不知道啊 qwq

那我们还需要回溯嘛？ 

其实我们可以不用回溯，用一种更加高级的方法：建反向边！

 

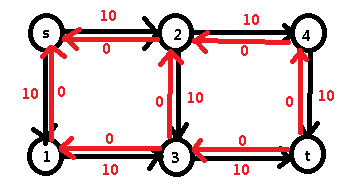
随后我们的每次增广，当某一条减去某个数时，它的相反边对应就加上那个数 。

 

假如我们又走了 s -> 2 -> 3 -> t 的错误路径的话：

 

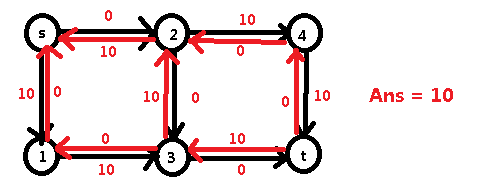
然后发现了什么？我们可以利用红色的边又找到一条增广路：s -> 1 -> 3 -> 2 -> 4 -> t ：

 

然后这下是真的找不到增广路了，整个算法就结束了 。

发现这个最后的情况是不是和我们之前最优走法剩下的情况是一样的？

说明我们可以利用反向边来实现无论怎么走都能求出最大流。

但是原理何在呢？为什么又要建反向边呢？

我们观察 ( 2 , 3 ) 这条边：在第一次增广的时候，正向边的容量已经流满了，不能再流了，而反向边的大小记录了这条边流了多少，可以粗略的记为正向边的容量都流到反向边那里去了；但是在第二次增广的时候，反向边又流满了，都流到正向边那里去了。这样一次往复操作，就是相当于 ( 2 , 3 ) 这条边没有流 。

其实到这里原理就出来了：在程序瞎跑的过程中，难免会走错路，但是我们还能通过反向边再走回来，也就是说这个反向边提供了反悔的机会，就相当于回溯的效果了 。

理解了反向边的作用，恭喜你已经理解了EK求解最大流算法的原理了。

 

现在还有一个小问题：怎么知道一条边的反向边是谁？

由于正向边和反向边是一起加的，所以反向边的编号与正向边的编号只相差1，那就好办了。

如果第一条边的编号是偶数，就有：

正向边的编号 ^ 1 == 反向边的编号；反向边的编号 ^ 1 == 正向边的编号。（为什么？）

那么接下来就来证明：

当正向边的编号为 2n 时反向边的编号为 2n+1。设 n 的二进制表示为 XXXXX，则 2n == n << 1 因此 2n 的二进制表示：XXXXX0，而 2n+1 的二进制表示：XXXXX1。那肯定（2n）^ 1 == 2n+1；(2n+1）^ 1 == 2n。

都讲完了，那么就附上完整代码：

#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
int read()
{
    char ch=getchar();
    int a=0,x=1;
    while(ch<'0'||ch>'9')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9')
    {
        a=(a<<1)+(a<<3)+(ch-'0');
        ch=getchar();
    }
    return a*x;
}
int n,m,s,t,u,v,w,ans,edge_sum=1;        //一定一定注意边数从1开始,保证第一条边的编号是偶数     
int head[100001],pre[200001],vis[100001],water[100001];
/*
pre[i]:点i的前一条边是谁,用来记录增广路径的
vis[i]:点i是否被遍历过
water[i]:从s到i的最大流是多少 
*/
struct node
{
    int to,next,dis;
}a[400001];
void add(int from,int to,int dis)                
{
    edge_sum++;
    a[edge_sum].next=head[from];
    a[edge_sum].to=to;
    a[edge_sum].dis=dis;
    head[from]=edge_sum;
}
bool bfs()                               //bfs找增广路 
{
    for(int i=1;i<=n;i++)                //初始化 
    {
        vis[i]=0;
        water[i]=0;
    }
    queue<int> q;
    q.push(s);
    vis[s]=1;
    water[s]=1e9;                        //起点s的流量无穷无尽 
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=a[i].next)
        {
            int v=a[i].to;
            if(a[i].dis==0||vis[v]) continue;  //如果这个点被遍历过,或者当前边的容量为0时,就跳过 
            water[v]=min(water[u],a[i].dis);   
            pre[v]=i;                    //当前路有可能是增广路,先记上再说 
            if(v==t) return 1;           //如果一直遍历到了t,说明存在增广路,直接返回 
            q.push(v);
            vis[v]=1;
        }
    }
    return 0;
}
void Add()                               //对增广路上的所有边进行减流量的操作         
{
    int x=t;                             //从终点t开始往前找 
    while(x!=s)                    
    {
        int edge=pre[x];                 //前驱边 
        a[edge].dis-=water[t];        
        a[edge^1].dis+=water[t];         //注意反向边要加上 
        x=a[edge^1].to;                  //反向边的终点就是当前点的前驱点 
    } 
    ans+=water[t];
}
int main()
{
    n=read();m=read();s=read();t=read();
    for(int i=1;i<=m;i++)
    {
        u=read();v=read();w=read();
        add(u,v,w);
        add(v,u,0);                      //反向边的容量一开始要设为0 
    }
    while(bfs()) Add();                  //如果找到增广路,那就增广 
    printf("%d",ans);
    return 0;
}

时间复杂度：O ( m² n )，能处理 1000 以内范围的网络流图 。

有没有更高效的算法呢？

既然我这么问了那么说明肯定有啦qwq 

考虑一下，我们的 EK 算法的原理是找增广路然后进行增广，但是这增广路是一条一条找的，对于下图来说可就麻烦大了：

 

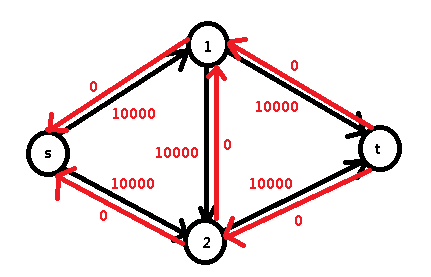
 都能一眼看出来先来一遍 s -> 1 -> t 增广 10000 的流量，然后再来一遍 s -> 2 -> t 增广 10000 的流量，然后就跑完了 。

但是想象很美好，现实很骨感；

假如我们走了 s -> 1 -> 2 -> t ：

 

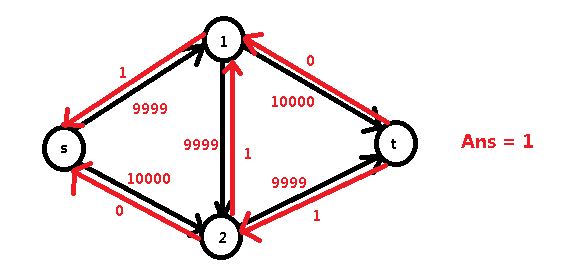
然后我们又很不幸，程序走了 s -> 2 -> 1 -> t：

 

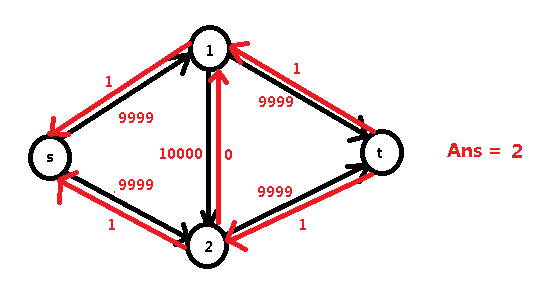
然后又走了 s -> 1 -> 2 -> t ……

这样算下来，原来两步搞定的事，程序傻傻的跑了 20000 次 ……

那么怎么高效的求出最大流呢？

Dinic 算法！

三. Dinic算法

为了学习这个高效的算法，我们要先引入分层图的概念：

就是从源点 s 出发开始 bfs，给每一个点分配一个深度 deep ，注意到一个点可能被多个点所连接，所以可能对应就有多个不同的 deep 值，我们保留最小的那个就好了。

如图：

 

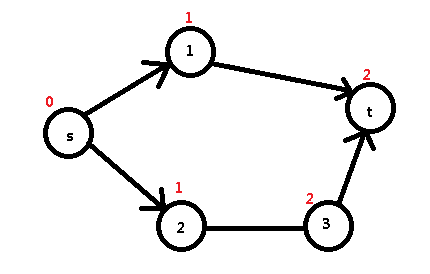
如果我们按照 s -> 2 -> 3 -> t 这条路线来更新每个点的 deep 值，那么 t 的 deep 值应该是 3，但是 s -> 1 -> t 这条路径可以使 t 的 deep 值更新为 2，所以我们舍弃 3 而保留 2；换句话说，一个点 u 的最小 deep 值一定是由 s -> u 的最短路径来更新的（若每条边的长度为 1），那么如果对于一条边 ( u , v ) ，若有 deep [ v ] == deep [ u ] + 1，则说明 ( u , v ) 这一条边是在 s -> t 的最短路径上的，然后我们在之后用 dfs 求增广路时就只走这样的边。

下面是 bfs 求深度的代码：

bool bfs()                         //bfs求每个点的深度 
{
    for(int i=1;i<=t;i++)          //初始化 
    {
        deep[i]=inf;
        vis[i]=0;
    }
    queue<int> q;
    deep[s]=0;                     //源点的深度记为0 
    vis[s]=1;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i;i=a[i].next)
        {
            int v=a[i].to;
            if(deep[v]>deep[u]+1&&a[i].dis)  //如果点v的深度能被更新,并且这条边的容量不为0 
            {
                deep[v]=deep[u]+1;           //此时v的深度一定比原来小了 
                if(!vis[v])
                {
                    q.push(v);
                    vis[v]=1;
                }
            }
        }
    }
    if(deep[t]==inf) return 0;               //如果t没被更新到,说明不存在增广路了,返回0 
    return 1;                                //否则的话就存在增广路 
}

 

如果我们 bfs 找到了增广路的话，我们就要用 dfs 去更新最大流啦，那怎么弄呢？