热题100_20230422

41、缺失的第一个正数

题目说明

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：
输入：nums = [1,2,0]
输出：3

示例 2：
输入：nums = [3,4,-1,1]
输出：2

示例 3：
输入：nums = [7,8,9,11,12]
输出：1

解题思路1：标记

题目要求时间复杂度为O(n)，且使用常数级别的额外空间，所以不能用一个新的数组或者HashSet来存储数字，也不可以对数组进行排序，最好是在给定数组上进行原地操作借助个别变量实现

标记的意思是，一个数组如果出现了[1 ~ n]的数字，那么就可以把对应的位置（假如排好序）设置一个标记，在本题中可以将标记置为负数，所以需要对负数先进行处理（反正没意义），对数组遍历完标记完数组之后，再遍历一遍标记好的数组，哪个位置没有被标记则说明缺乏这个位置对应的数字

• 首先对负数和0进行处理，将其处理成n + 1，方便后续的标记
• 然后遍历数组，当出现了在[1 ~ n]之间的数字nums[i]时，就把对应位置nums[nums[i] - 1]置为负数。应该注意的是，在一开始数组是没有负数的，在操作后可能出现还没遍历的数字变成负数的情况，因此在取nums[i]时应取绝对值
• 最后对处理好的数组进行遍历，如果对应的位置 i 不是负数，返回其对应的i + 1即可，如果遍历结束都是满足条件的，则返回nums.length + 1

解题思路2：交换

交换的思路有点类似排序，但并没有要求对整个数组进行排序，只是把符合条件[1 ~ n]的数字放到正确的位置即可，并把正确位置的数字换过来，重新对其进行判断以及后续的操作，直到该位置数字不符合条件，或者当前位置的数字就是应该放在这个位置，因此在循环中要额外加一个判断nums[nums[i] - 1] != nums[i]，放对了当然不用再交换，否则就是一个死循环了。

因为换好位置的数字今后再遇到是不用再操作的，可以直接跳过，所以实际上最多的交换次数就是nums.length，符合O(n)的时间复杂度

在交换完位置对数组处理好之后，再一次遍历数组，看位置是否对应到了正确的数字，如果没对应到，返回该位置对应的数字i + 1即可，否则返回nums.length + 1

48、旋转图像

题目说明

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

解题思路

要求使用原地算法，所以不能用一个新的数组，只能在原先的基础上修改。可以很清晰的看出来，位置的变化是有规律可循的，且是分为四个板块的，如下图所示

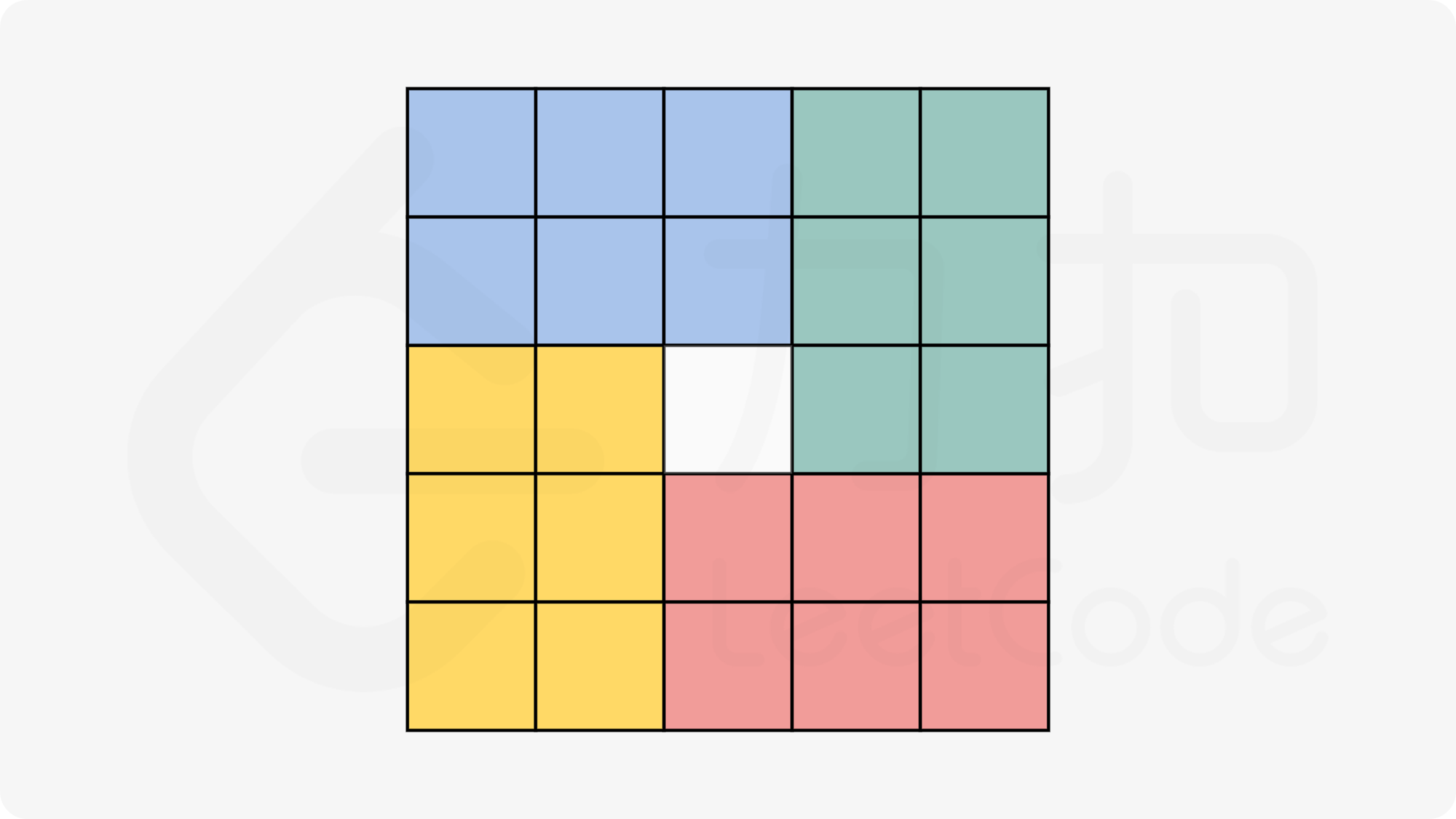
那么我们可以依据规律找出四个位置，遍历完一个板块即可，每次进行四次更替，四个位置可推出分别是

(i, j)，(j, n - i - 1)，(n - i - 1, n - j - 1)，(n - j - 1, i)

(i, j)为第一个板块，可以设置出以下两层循环将其遍历完

for (int i = 0; i < n / 2; i++) {
    for (int j = 0; j < (n + 1) / 2; j++) {
    }
}

73、矩阵置零

题目说明

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

解题思路1：额外的数组标记

可以知道，如果当某一位置出现0时，对应的行和列都置为0，那么就设置一个行标记数组row和一个列标记数组col，当matrix[i][j] == 0时，将row[i]和col[j]置为0。等数组遍历完之后，依据row和col把matrix数组置零即可

解题思路2：将第一行和第一列用于标记

原理就是把matrix的第一列和第一行用于标记，那么就需要额外的变量来标记第一行和第一列需不需要变成0，设置变量row和col，先对第一行和第一列进行遍历，如果有0则对变量进行标记修改。此后对第二列第二行开始的数组进行遍历并在第一行和第一列标记（标记0），处理好之后依据第一行第一列对后面的子矩阵进行修改，最后根据row和col标记对第一行和第一列进行修改

240、搜索二维矩阵 II

题目说明

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

解题思路1：暴力

暴力遍历，把matrix直接过一遍，找到就返回true，没有则返回false

解题思路2：递归

编写search函数进行递归处理，递归的返回条件分为三类

• 超限或者已经找过当前位置：先判断位置是否是合法的是否超出范围，通过一个同样大小的boolean数组来判定当前位置是否被遍历过，如果超限或遍历过则返回false
• 判定当前位置是不是targer，是则返回true
• 判定是否当前位置大于target，是的话则返回false，表示不能往这个方向找了
• 还小的话可以从两个方向找，于是返回当前位置的正下方坐标和正右方坐标

解题思路3：z字查找

设定初始位置为矩阵的右上角，可以理解为是一个中间的位置，此时坐标为（0，matrix[0].length - 1）

反复对当前的位置与target进行判断，如果等于targer则返回true，如果小于target则说明当前行的数据都小于targer，target只可能出现在下一行，row++；如果大于target则说明当前列的数据都大于targer，target只可能出现在左边，col--。当col < 0或者row > martrix.length - 1时则说明target不存在，返回false