容器的主要用途就是对其中存储的数据进行“增删改查”。那么不同的数据结构的设计,增删改查的效率是不一样的。
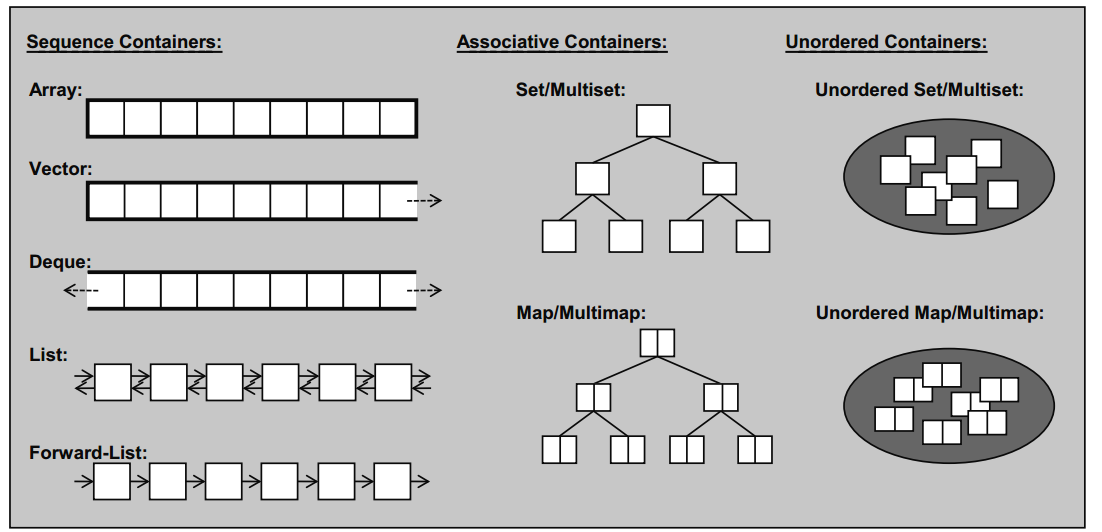
顺序容器
元素按顺序存储,支持动态调整大小和顺序访问
【arry-静态数组】
存储结构---所有的元素会严格按照内存地址线性排列,使用连续的内存空间存储数据元素。
创建了arry,编译的时候就固定了大小,不支持动态扩展。比较适合大小固定并且已知大小的数据集合。
⚠️注意:对两个array执行swap会交换两个数组范围内的元素,但是不会改变内存地址,也就是不会改变两个容器各自的迭代器的依附属性。
array 和 C++语法中的[]符号无限接近,访问速度与普通数组几乎无差,只是多了 STL 接口。支持begin(), end(), front(), back(), at(), empty(), data(), fill(), swap(), ... 等等标准接口
| 方法 | 含义 |
|---|---|
operator[] / at() |
随机访问元素;at 有越界检查 |
size() |
返回固定大小(编译期常量) |
front() / back() |
第一个和最后一个元素 |
fill(value) |
所有元素填充为 value |
begin()/end() |
返回起始/结束迭代器 |
cbegin()/cend() |
常量迭代器(只读) |
data() |
返回指向原始数组的指针 |
swap(array) |
与另一个 std::array 交换内容 |
empty() |
如果 size 为 0,返回 true |
举例:
//声明方式
std::array<int, 4> arr1 = {1, 3, 4, 9}; // 创建了一个元素为int类型,一共四个元素的确定数组
std::array<int, 4> arr2 = {}; // 创建了一个元素为int类型,一共四个元素,但是元素未知的数组
std::array<int, 4> arr3 = {5}; // 创建了一个元素为int类型,一共四个元素,但是只有第一个元素已知,其余未知的数组
//基本操作
arr1.at(2); // 访问位置2处的元素
arr1[3]; // 访问位置3处的元素
arr1.size(); // 获取数组大小
arr1.front(); //获取第一个元素
arr1.back(); // 获取最后一个元素
arr2.fill(1); // 全部填充1
【vector-动态数组】
存储结构---所有的元素会严格按照内存地址线性排列,使用连续的内存空间存储数据元素,这样就表明可以使用普通的++或者--指针来访问里面的元素(与arry相同)
与arry不同的地方就是它的存储空间可以自动调整,也就是vector就是能够动态调整大小的arry。
template<typename T>
class Vector {
T* _start; // 指向数据块起始地址
T* _finish; // 当前元素末尾(下一可插入位置)
T* _end_of_storage; // 总容量末尾
};
✅扩容机制:vector使用动态分配的array,当现有的空间无法满足增长需求的时候,会重新分配一个更大的array(C++里面一般设置为2倍),然后把元素移动过去。也就是vector的容量一般会比实际的size大。
重新分配内存的操作步骤:
(1)分配新内存
(2)拷贝旧数据到新内存
(3)释放旧内存
优缺点---使用vector访问随即元素和尾部添加删除元素效率高,但是在尾部以外的地方增删元素效率很低,并且迭代器的一致性比较差。
| 方法 | 含义 |
|---|---|
vec.begin() |
返回指向首元素的迭代器 |
vec.end() |
返回指向末尾后一个位置的迭代器 |
vec.front() |
返回首元素(引用) |
vec.back() |
返回末尾元素(引用) |
vec.push_back(x) |
在末尾插入一个元素 |
vec.pop_back() |
删除末尾一个元素 |
vec.size() |
当前元素个数 |
vec.empty() |
返回是否为空 |
vec.clear() |
清空所有元素 |
举例:
//声明方式
//底层代码提供了template<type T> ==>可以支持创建不同数据类型的动态数组
vector<int> vec;
vector<char> vec;
vector<pair<int,int> > vec;
struct node{...};
vector<node> vec;
vector<int> v1; // 空向量
vector<int> v2(5); // 5 个元素,值为 0
vector<int> v3(5, 42); // 5 个元素,每个为 42
vector<int> v4 = {1, 2, 3, 4}; // 列表初始化
【list-双向链表】
存储结构---list的底层结构是一个双向链表,每个元素存储在独立的节点中,节点之间通过前向指针和后向指针连接;
//底层结构
template<typename T>
struct Node {
T val;
Node* prev;
Node* next;
};
优缺点---支持在任意位置快速的插入和删除元素,并且支持双向遍历。但是list不支持随机访问,我们要访问一个元素的话,需要从一个已知元素(begin/end)朝一个方向遍历,直到遍历到要访问的元素,此外,list会需要更多的内存空间,用来保存各个元素的关联信息。
| 方法 | 功能说明 |
|---|---|
push_back(val) |
在尾部插入元素 |
push_front(val) |
在头部插入元素 |
pop_back() |
删除尾部元素 |
pop_front() |
删除头部元素 |
insert(pos, val) |
在指定位置插入元素(迭代器) |
erase(pos) |
删除指定位置的元素(迭代器) |
remove(val) |
删除所有值为 val 的元素 |
clear() |
清空容器 |
size() |
返回元素个数 |
empty() |
检查是否为空 |
begin()/end() |
获取首/尾迭代器 |
rbegin()/rend() |
反向迭代器 |
sort() |
排序(必须自己实现比较器) |
unique() |
去除连续重复元素 |
merge(other) |
合并两个已排序的 list |
reverse() |
反转 list 顺序 |
举例:
//声明方式
list<int> l = {1, 2, 3};
std::list<int> l1; // 空链表
std::list<int> l2(5); // 5个默认值为0的int元素
std::list<int> l3(5, 10); // 5个值为10的元素
std::list<int> l5(l); // 拷贝构造
l.push_back(4);
l.push_front(0);
for (int x : l) cout << x << " "; // 输出 0 1 2 3 4
【forward_list-单向链表】
存储结构---forward_list与list的存储结构类似,相比于 list 的核心区别是它是一个单链表,因此每个节点只存储一个后向指针。每个元素只会与相邻的下一个元素关联!
由于关联信息少了一半,因此 forward_list 占用的内存空间更小,且插入和删除的效率稍稍高于 list。作为代价,forward_list 只能单向遍历。
//底层结构
template<typename T>
struct Node {
T value;
Node* next;
};
?设计 forward_list 的目的是为了达到不输于任何一个C风格手写链表的极值效率!为此,forward_list 是一个最小链表设计,没有size()接口,因为内部维护一个size变量会降低增删元素的效率。所以要想知道大小就需要遍历。
总结就是:list 兼顾了接口丰富性牺牲了效率,而 forward_list 舍弃了不必要的接口只为追求极致效率。
| 方法 | 功能说明 |
|---|---|
push_front(val) |
插入头部元素 |
pop_front() |
删除头部元素 |
insert_after(pos, val) |
在指定位置后插入 |
erase_after(pos) |
删除指定位置后的元素 |
remove(val) |
删除所有值为 val 的元素 |
unique() |
删除连续重复元素 |
sort() |
排序 |
reverse() |
反转顺序 |
merge(list2) |
合并两个升序的 forward_list |
before_begin() |
获取头结点前的一个迭代器(用于插入) |
begin()/end() |
获取首/尾迭代器 |
empty() |
判断是否为空 |
clear() |
清空链表 |
举例:
//声明方式
forward_list<int> fl = {1, 2, 3};
std::forward_list<int> fl1; // 空单向链表
std::forward_list<int> fl2 = {0, 0, 0, 0, 0}; // 用初始化列表填充,不能写 forward_list<int> fl(5);
std::forward_list<int> fl3;
fl3.assign(5, 100); // 5个值为100的元素
std::forward_list<int> fl4(fl); //拷贝构造
fl.push_front(0); // 插入头部
auto it = fl.before_begin(); // 必须使用前驱节点进行插入
fl.insert_after(it, -1);
for (int x : fl) cout << x << " "; // 输出 -1 0 1 2 3
【deque-双端队列】
存储结构---不同的库对deque的实现可能不同,但大体上都是使用分段连续内存块 + 中控表(map)的结构管理数据,内存块称为 “缓冲区”(buffer):每个 buffer 大小固定,通常 512 字节或一个指针大小的整数倍,中控结构是一个指针数组,称为 map(控制中心):它记录了所有 buffer 的地址。通过一个中控结构(map-like)连接这些块,支持前后动态扩容。vector使用的是单一的array,deque则会使用很多个离散的array来组织数据,因此vector是连续的,deque 则是分段连续,也就是deque 会维护不同 array 之间的关联信息。由于deque不保证存储区域一定是连续的,因此不能用指向元素的普通指针做++和--操作。
//底层结构
//控制结构
T** map; // map 是指针数组,指向多个 buffer
size_t map_size;
_Deque_iterator start, finish;
template<typename T>
struct _Deque_iterator {
T* cur; // 当前元素指针
T* first; // 当前 buffer 的起始地址
T* last; // 当前 buffer 的末尾地址
T** node; // 当前 buffer 在 map 中的指针位置
};
扩容机制:
(1)当我们执行 push_back() 或 push_front() 等操作时检查空间,当前 buffer 满了,就需要:申请一个新的 buffer 内存块,allocate_node(),将其指针挂到 map 的合适位置上,更新迭代器指针,如 start 或 finish。
(2)当 map 本身不够大时,分配更大的 map、拷贝旧指针、调整 start/finish 的 node 指针、删除旧 map。
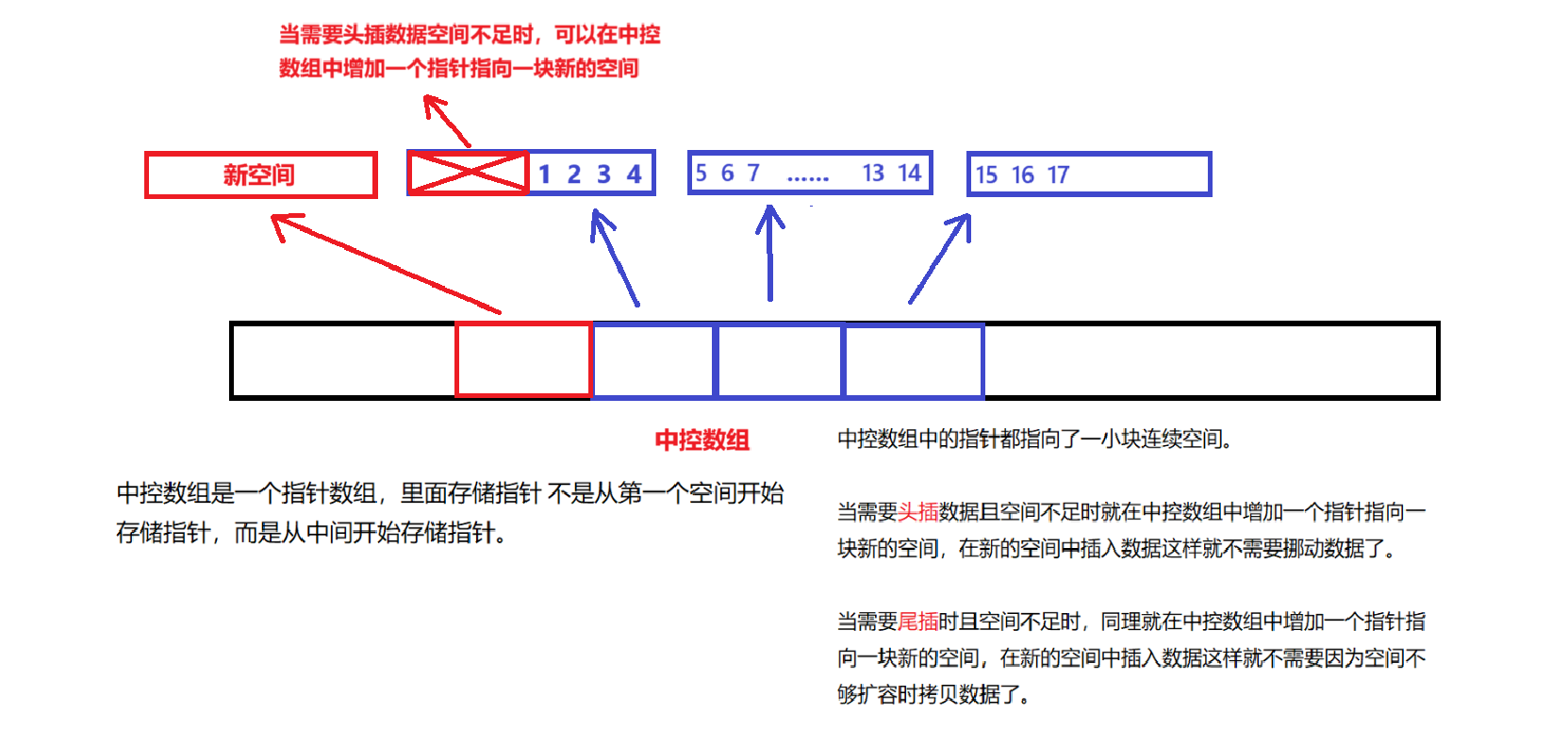
支持头尾两端高效插入/删除(都是 O(1) 时间复杂度,摊还)、支持随机访问(O(1))、自动扩展容量(不需要手动扩容),但是deque 并不适合遍历。因为每次访问元素时,deque 底层都要检查是否触达了内存片段的边界,造成了额外的开销
| 分类 | 方法 | 描述 |
|---|---|---|
| 构造函数 | deque<T> d |
默认构造空队列 |
deque<T> d(n) |
n 个默认值元素 | |
deque<T> d(n, val) |
n 个 val 元素 | |
deque<T> d{...} |
列表初始化 | |
| 元素访问 | d[i]、d.at(i) |
访问第 i 个元素 |
d.front() / d.back() |
访问头部/尾部元素 | |
| 修改 | d.push_back(val) |
末尾插入元素 |
d.push_front(val) |
头部插入元素 | |
d.pop_back() / pop_front() |
删除尾部 / 头部元素 | |
d.insert(pos, val) |
插入元素到指定位置(迭代器) | |
d.erase(pos) |
删除指定位置元素 | |
d.clear() |
清空容器 | |
| 大小 | d.size() / d.empty() |
返回元素个数 / 是否为空 |
| 其他 | d.swap(other) |
与另一个 deque 交换 |
| 迭代器 | begin(), end(), rbegin(), rend() |
支持正向、反向迭代 |
举例:
//声明方式
deque<int> dq = {1, 2, 3};
deque<string> names;
deque<pair<int, int>> pointPairs;
deque<int> d1; // 空
deque<int> d2(3); // [0, 0, 0]
deque<int> d3(3, 5); // [5, 5, 5]
deque<int> d4{1, 2, 3, 4}; // [1, 2, 3, 4]
dq.push_front(0); // 头部插入
dq.push_back(4); // 尾部插入
for (int x : dq) cout << x << " "; // 输出 0 1 2 3 4
dq.pop_front(); // 删除 0
dq.pop_back(); // 删除 4
cout << "\nsize: " << dq.size(); // 输出 3
常见使用deque的题目:
滑动窗口最大值(如单调队列)
LRU 缓存淘汰策略
BFS(广度优先搜索)队列
双向模拟队列系统
【性能对比】
| 操作 | deque |
vector |
list |
|---|---|---|---|
| 随机访问 | O(1) | O(1) | ❌ 不支持 |
| 尾部插入/删除 | O(1) | O(1) | O(1) |
| 头部插入/删除 | O(1) | O(n) | O(1) |
| 中间插入/删除 | O(n) | O(n) | O(1)(已知位置) |
| 内存结构 | 分段数组 | 连续内存 | 双向链表 |
关联容器
元素以键值对方式存储,对所有元素的检索都是通过元素的 key 进行的(而非元素的内存地址),实现高效查找;数据存储有序,底层实现是平衡二叉树(红黑树)
【map-键值对容器】
存储结构---map通过底层的红黑树数据结构来将所有的元素按照 key 的相对大小进行排序,所实现的排序效果也是严格弱序特性,为此,开发者需要重载 key 的<运算符或者模板参数中的 class Compare。【解释:插入、查找、删除等操作都依赖于 key 之间的大小比较。比较规则默认使用operator<,因为如果你的 key 是用户自定义类型(struct/class),STL 默认不知道怎么排序。也可以通过模板参数传入自定义的比较器。比较规则定义了 map 的排序标准,必须满足“严格弱序”的条件,才能构建稳定可靠的有序结构。】
🚫严格弱序 ≠ 全序,不要求所有元素都可以比较大小
| 条件 | 描述 |
|---|---|
| 非自反性 | !(x < x) 必须为 true(即,元素不能小于自己) |
| 反对称性 | 如果 x < y 为 true,则 y < x 必须为 false |
| 传递性 | 如果 x < y 且 y < z,则 x < z |
| 不可比性 | 如果 !(x < y) 且 !(y < x),那么 x 和 y 被认为是等价的,不是相等,而是“无法区分大小” |
当 key 为自定义类型(如 struct),必须提供比较方式(operator< 或自定义比较器)。
struct Point {
int x, y;
bool operator<(const Point& other) const {
return x < other.x || (x == other.x && y < other.y);
}
};
std::map<Point, string> pointMap; // key的类型是Point,里面自定义了比较器
优缺点---大多数情况下,map的查找、插入、删除操作都在 对数时间 O(logN) 内完成,由于底层是红黑树结构不会退化为链表形式。支持自动排序,范围查询。但是查询效率比其他的容器效率低一些,并且占用的内存比较大(使用红黑树结构+指针进行管理),删除和插入效率也不是最好的。就是更加稳定!
| 函数原型 | 说明 | 返回值 / 备注 |
|---|---|---|
size() |
返回元素个数 | size_t 类型 |
empty() |
判断是否为空 | true 或 false |
clear() |
清空所有元素 | 无 |
insert(pair<key, value>) |
插入键值对 | pair<iterator, bool> |
erase(key) |
删除指定 key 的元素 | 删除数量(0 或 1) |
erase(iterator) |
删除指定位置元素 | 返回下一个有效迭代器 |
find(key) |
查找 key 对应元素 | 找到返回迭代器,找不到返回 end() |
count(key) |
判断 key 是否存在 | 0 或 1 |
operator[] |
访问或插入 key 对应的 value | 如果不存在 key,则默认插入 |
at(key) |
安全访问(若 key 不存在抛异常) | 返回引用,异常:out_of_range |
begin() / end() |
返回迭代器(起始 / 末尾) | 双向迭代器 |
rbegin() / rend() |
反向迭代器(逆序遍历) | 反向双向迭代器 |
lower_bound(key) |
返回 >= key 的首个元素迭代器 |
支持区间查找 |
upper_bound(key) |
返回 > key 的首个元素迭代器 |
|
equal_range(key) |
返回 pair<lower, upper> | 用于范围操作 |
swap(map2) |
与另一个 map 交换内容 | 无 |
emplace(key, value) |
原地构造元素(C++11起) | 返回 pair<iterator, bool> |
emplace_hint(pos, key, value) |
提供插入位置提示的原地构造 | 返回 iterator |
举例:
std::map<std::string, int> ageMap;
ageMap["Tom"] = 20;
【set-集合容器】
存储结构---它的底层结构是红黑树,和 map 不一样的是,set 是直接保存 value 的,或者说,set 中的 value 就是 key。set 中的元素必须是唯一的,不允许出现重复的元素,且元素不可更改,但可以自由插入或者删除。并且元素按照一定规则自动排序(默认用 < 运算符,从小到大)
set和map类似,具有稳定的插入、删除、查找操作复杂度,都是 O(log n)。 插入效率低于哈希表,无法直接访问下标,对比map,由于map需要维护pair<key, value> 结构,比单一 key 的 set稍复杂,占用空间更多。set只关心元素是否存在,map可以记录额外的关联信息。
| 函数原型 | 功能说明 | 返回值 / 说明 |
|---|---|---|
insert(val) |
插入元素(自动排序+去重) | pair<iterator, bool> |
erase(val) |
删除指定值的元素 | 删除个数(0或1) |
erase(iterator) |
删除指定位置元素 | 返回下一个有效迭代器 |
find(val) |
查找元素 | 找到返回迭代器,未找到返回 end() |
count(val) |
判断某个值是否存在 | 返回 0 或 1 |
size() |
返回元素个数 | size_t 类型 |
empty() |
判断容器是否为空 | true / false |
clear() |
清空所有元素 | 无 |
begin() / end() |
返回迭代器(起始 / 尾后) | 支持前向遍历 |
rbegin() / rend() |
反向迭代器 | 逆序遍历 |
lower_bound(val) |
返回 >= val 的第一个元素 | iterator |
upper_bound(val) |
返回 > val 的第一个元素 | iterator |
equal_range(val) |
返回 pair<lower, upper> | 可用于区间遍历 |
emplace(val) |
原地构造插入(C++11) | pair<iterator, bool> |
swap(set2) |
与另一个 set 交换数据 | 无 |
举例:
std::set<int> s1; // 创建一个空的整数 set
std::set<std::string> s2; // 创建一个空的字符串 set
std::set<int> s = {3, 1, 4, 1, 5, 9}; // 自动去重、排序 ==> s 中为:{1, 3, 4, 5, 9}
//自定义规则
struct cmp {
bool operator()(const int &a, const int &b) const {
return a > b; // 降序排序
}
};
std::set<int, cmp> s = {5, 2, 8, 1}; // 输出顺序:8 5 2 1
//利用数组初始化
int arr[] = {4, 2, 5, 2, 3};
std::set<int> s1(arr, arr + 5);
std::vector<int> v = {10, 20, 10, 30};
std::set<int> s2(v.begin(), v.end());
无序容器
基于哈希表实现,以哈希表形式存储,查找性能更好,但数据无序
【unordered_map-基于哈希实现】
存储结构---map以红黑树作为底层结构组织数据,而 unordered_map 以哈希表(通常使用开链法 + vector)(hash table)作为底层数据结构来组织数据,其中哈希冲突的解决办法:默认使用开链法:一个桶存多个元素链表
优缺点:
- unordered_map 不支持排序,在使用迭代器做范围访问时(迭代器自加自减)效率更低;
- 但 unordered_map 直接访问元素的速度更快(尤其在规模很大时),因为它通过直接计算 key 的哈希值来访问元素,是O(1)复杂度
map 增删元素的效率更高,unordered_map 访问元素的效率更高,另外,unordered_map 内存占用更高,因为底层的哈希表需要预分配足量的空间。
| 函数原型 | 功能说明 |
|---|---|
insert({key, value}) |
插入一个键值对(不覆盖旧值) |
operator[] / at(key) |
插入或访问 key 对应的 value |
erase(key) / erase(it) |
删除指定键或迭代器位置元素 |
find(key) |
查找 key,返回迭代器 |
count(key) |
判断 key 是否存在(返回 0 或 1) |
size() / empty() / clear() |
容器状态操作 |
begin() / end() |
迭代器遍历 |
emplace(key, value) |
原地构造,性能优于 insert |
bucket_count() |
哈希桶的数量 |
load_factor() |
当前负载因子(元素 / 桶数) |
rehash(n) |
重新分配至少 n 个桶 |
reserve(n) |
预分配空间避免频繁扩容 |
举例:
std::unordered_map<std::string, int> umap1;
std::unordered_map<std::string, int> umap2 = {
{"one", 1},
{"two", 2},
{"three", 3}
};
使用场景:
频繁插入/查找 key-value 映射,如计数器(词频、字符统计等)
不关心元素顺序的哈希查找场景
替代 map 获取更高性能
【unordered_set-基于哈希实现】
存储结构---以哈希表(开链法)作为底层结构,每个元素在容器中唯一,不允许重复。
元素顺序不固定,由哈希函数决定。查找效率极高,平均复杂度为 O(1)。
| 函数原型 | 作用描述 |
|---|---|
insert(val) |
插入元素(自动去重) |
emplace(val) |
原地构造,性能优 |
erase(val) |
删除指定元素 |
find(val) |
查找元素,返回迭代器 |
count(val) |
返回是否存在(0或1) |
size() / empty() |
获取大小 / 是否为空 |
clear() |
清空容器 |
begin() / end() |
迭代器遍历 |
load_factor() |
查看当前负载因子 |
rehash(n) / reserve(n) |
手动控制桶数和容量 |
举例:
std::unordered_set<int> us1;
std::unordered_set<int> us2 = {4, 2, 7, 2}; // 自动去重,us = {2, 4, 7}
//自定义哈希函数初始化
struct Point {
int x, y;
bool operator==(const Point &p) const {
return x == p.x && y == p.y;
}
};
struct HashFunc {
size_t operator()(const Point &p) const {
return hash<int>()(p.x) ^ hash<int>()(p.y << 1);
}
};
std::unordered_set<Point, HashFunc> points;
容器适配器
🧩作为适配器,需要指定底层容器才能实例化。
template<
class T, // 数据类型
class Container = std::deque<T> // 底层容器类型,默认为 deque
> class stack/queue;
template<
class T, // 元素类型
class Container = vector<T>, // 底层容器,默认是 vector
class Compare = less<typename Container::value_type> // 比较器
> class priority_queue;
【stack-栈】
存储结构---遵循LIFO设计原则的容器适配器,也即只能从一端插入和删除;vector,list,deque 皆可作为stack的底层容器,底层容器必须要支持在尾部的插入和删除,默认使用deque;可见它并不是一种独立的数据结构,而是对底层容器(如 deque 或 vector)的一种包装,只暴露栈的操作接口。
优缺点---使用简单,操作符合栈模型,插入、删除操作效率高,可以自由选择底层容器,但是只能访问栈顶,不能随机访问,不支持遍历,无法初始化时指定初始数据内容
| 接口 | 功能描述 |
|---|---|
push(val) |
压栈(插入元素) |
pop() |
出栈(移除栈顶元素) |
top() |
返回栈顶元素(不删除) |
empty() |
判断栈是否为空 |
size() |
返回栈中元素数量 |
emplace(args...) |
原地构造一个元素压栈(C++11 起) |
举例:
stack<int> s1; // 空栈
stack<int, vector<int>> s2; // 指定底层容器为 vector
stack<int, deque<int>> s3({1, 2, 3}); // 用 deque 初始化
常见使用场景:
括号匹配、表达式求值
DFS遍历(非递归写法)
浏览器前进/后退功能实现
压栈回溯、状态保存等算法逻辑
【queue-队列】
存储结构---遵循FIFO设计原则的容器适配器,也即只能从一端插入、从另一端删除;vector,list,deque 皆可作为queue的底层容器,默认为 deque
优缺点---符合 FIFO 的使用需求,接口简单,操作直观,可自由选择底层容器;但是不能随机访问内部元素,不能遍历,插入删除只能在队尾/队首
| 成员函数 | 说明 |
|---|---|
push(x) |
入队:将元素插入队尾 |
pop() |
出队:删除队首元素 |
front() |
返回队首元素 |
back() |
返回队尾元素 |
empty() |
判断队列是否为空 |
size() |
返回队列中的元素个数 |
emplace(x) |
原地构造一个元素到队尾(C++11) |
举例:
//声明
std::queue<int> q1; // 默认构造,使用 deque
std::deque<int> d = {1, 2, 3};
std::queue<int> q2(d); // 用已有 deque 初始化
std::queue<int, std::list<int>> q3; // 指定底层容器为 list
使用场景:
任务调度:生产者-消费者模型
宽度优先搜索(BFS)
消息队列、事件队列
控制流程排队(如打车、排号系统)
【priority_queue-优先队列(默认大顶堆)】
存储结构---遵循最高优先级先出;priority_queue在内部维护一个基于二叉树的大顶堆数据结构,在这个数据结构中,最大的元素始终位于堆顶部,且只有堆顶部的元素才能被访问和获取,默认使用 vector 作为底层容器,也就是在 vector 上使用堆算法将 vector 中元素构造成大顶堆的结构。核心特点在于其严格弱序特性:即priority_queue保证容器中的第一个元素始终是所有元素中最大的,每当有新元素进入,它都会根据既定的排序规则找到优先级最高的元素,并将其移动到队列的队头。
优缺点---获取最大(或最小)元素效率高,插入/删除元素复杂度是 O(logN),灵活的比较器支持自定义优先级;不支持遍历,不支持随机访问,不能直接修改堆中已有元素的值
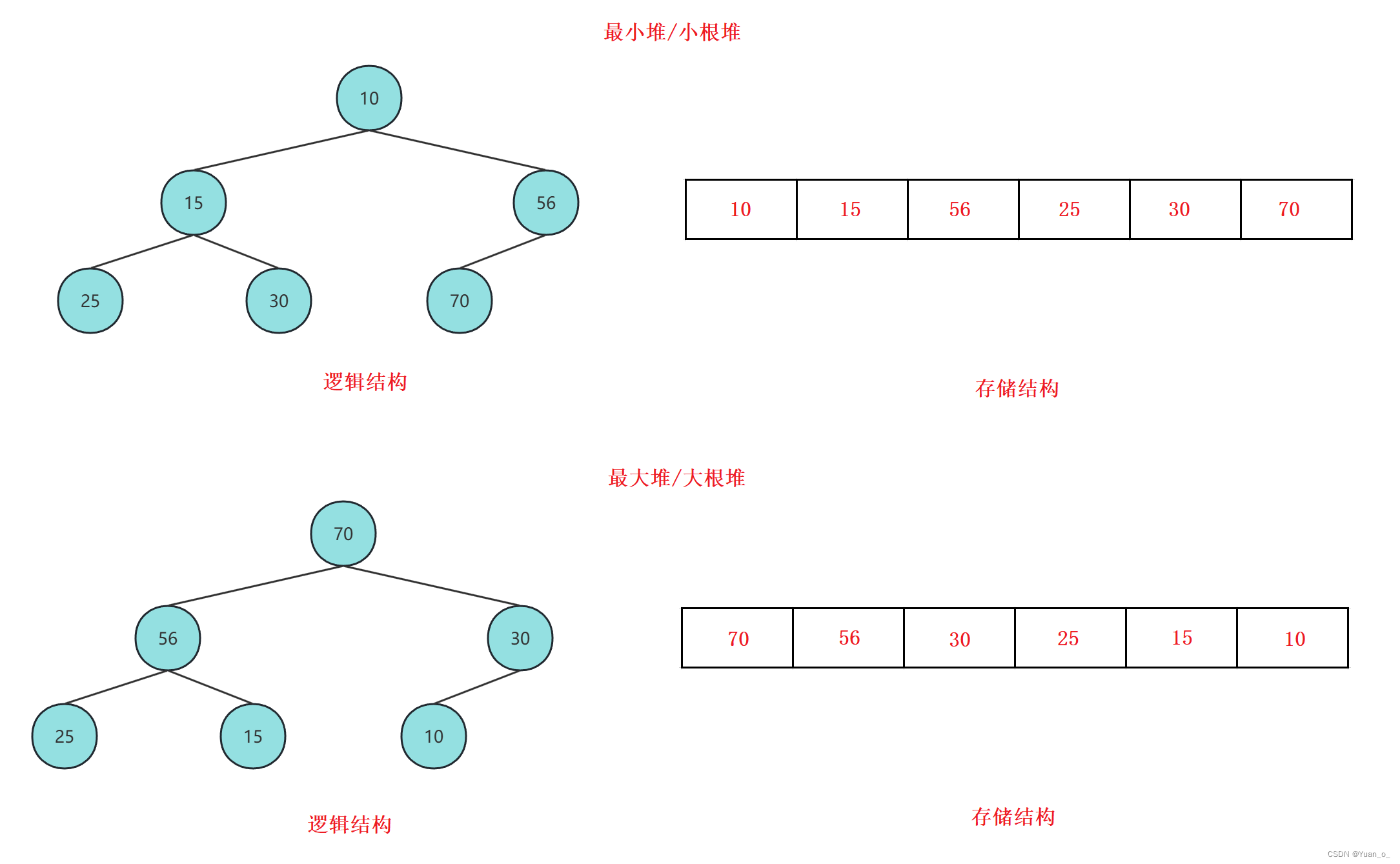
①堆中某个节点的值总是大于或等于其父节点的值,称为最小堆/小根堆
②堆中某个节点的值总是小于或等于其父节点的值,称为最大堆/大根堆
③堆总是一棵完全二叉树
| 成员函数 | 作用描述 |
|---|---|
push(x) |
插入元素到堆中 |
pop() |
移除堆顶元素 |
top() |
获取堆顶元素(优先级最高) |
empty() |
判断堆是否为空 |
size() |
返回堆中元素数量 |
emplace(args...) |
原地构造元素(C++11) |
举例:
priority_queue<int> pq1; //默认最大堆
priority_queue<int, vector<int>, greater<int>> minHeap; //最小堆实现方式
//自定义类型的优先级队列
struct Node {
int val;
int priority;
};
struct cmp {
bool operator()(const Node& a, const Node& b) {
return a.priority < b.priority; // priority大的优先
}
};
priority_queue<Node, vector<Node>, cmp> pq2;
使用场景:
堆排序
Dijkstra 最短路径算法
A* 搜索算法
任务调度系统
Top-K 问题


 浙公网安备 33010602011771号
浙公网安备 33010602011771号