排序算法一：直接插入排序

转自：http://blog.csdn.net/lg1259156776/

插入排序(Insert Sorting)

基本思想

每步将一个待排序的对象,按其排序码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。

分类

根据寻找插入位置方法分为

• 直接插入排序
• 折半（二分）插入排序
• 希尔插入排序

直接插入排序

基本思想

当插入第i(i≥1)i(i≥1)个对象时,前面的V[0],V[1],…,V[i−1]V[0],V[1],…,V[i−1]已经排好序。这时,用V[i]V[i]的排序码与V[i−1],V[i−2],…,V[0]V[i−1],V[i−2],…,V[0]的排序码顺序进行比较,找到插入位置即将V[i]V[i]插入,原来位置上的对象向后顺移。

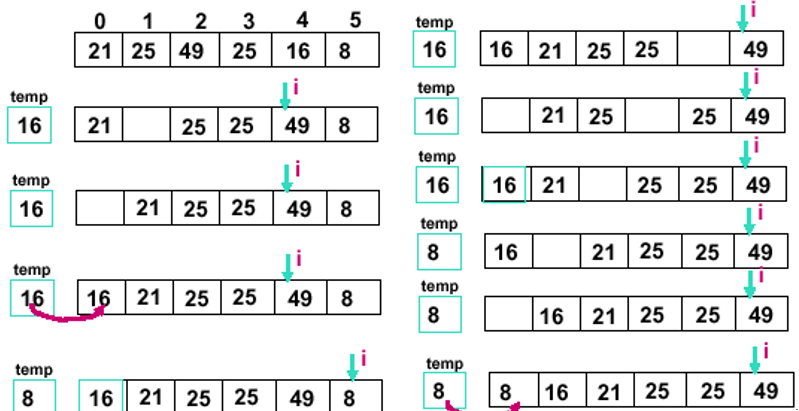
直接插入排序图示

从上到下，分别展示了直接排序算法的所有可能的过程，包括相同排序码的排序方式（保持了原来的顺序，说明是稳定排序）以及in-place操作中的元素移动等。

直接插入排序算法分析

设待排序对象个数为nn,则该算法的主程序执行n−1n−1趟排序码比较次数和对象移动次数与对象排序码的初始排列有关。

• 最好情况下,排序前对象已经按照要求的有序。比较次数(KCN):n−1n−1 ; 移动次数(RMN):为00。则对应的时间复杂度为O(n)O(n)。
• 最坏情况下,排序前对象为要求的顺序的反序。第ii趟时第ii个对象必须与前面ii个对象都做排序码比较,并且每做1次比较就要做1次数据移动（具体可以从下面给出的代码中看出）。比较次数(KCN):∑n−1i=1i=n(n−1)2≈n22∑i=1n−1i=n(n−1)2≈n22 ; 移动次数(RMN):为∑n−1i=1i=n(n−1)2≈n22∑i=1n−1i=n(n−1)2≈n22。则对应的时间复杂度为O(n2)O(n2)。
• 如果排序记录是随机的，那么根据概率相同的原则，在平均情况下的排序码比较次数和对象移动次数约为n24n24，因此，直接插入排序的时间复杂度为O(n2)O(n2)。

直接插入排序算法的特点

• 它是稳定排序，不改变相同元素原来的顺序。
• 它是in-place排序，只需要O(1)O(1)的额外内存空间。
• 它是在线排序，可以边接收数据边排序。
• 它跟我们牌扑克牌的方式相似。
• 对小数据集是有效的。

To save memory, most implementations use an in-place sort that works by moving the current item past the already sorted items and repeatedly swapping it with the preceding item until it is in place.

直接排序的代码（C++版本）

伪代码如下：

for i = 1, n
j = i
while(j > 0 and E[j] < E[j-1])
     swap(E[j], E[j-1])
     j--

C++代码

#include <iostream>
#include <iomanip>

using namespace std;

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

void insertion(int a[], int sz)
{
    for(int i=1; i  < sz; i++) {
        int j = i;
        while(j > 0 && (a[j] < a[j-1])) {
            swap(a[j], a[j-1]);
            j--;
        }
        cout << endl;
        for (int k = 0; k < sz; k++) cout << setw(3) << a[k];
    }
}

int main()
{
    int a[] = { 15, 9, 8, 1, 4, 11, 7, 12, 13, 6, 5, 3, 16, 2, 10, 14};
    int size = sizeof(a)/sizeof(int);
    for (int i = 0; i < size; i++) cout << setw(3) << a[i];
    insertion(a, size);
    cout << endl;
    return 0;
}

过程输出：

15  9  8  1  4 11  7 12 13  6  5  3 16  2 10 14 

  9 15  8  1  4 11  7 12 13  6  5  3 16  2 10 14 

  8  9 15  1  4 11  7 12 13  6  5  3 16  2 10 14 

  1  8  9 15  4 11  7 12 13  6  5  3 16  2 10 14 

  1  4  8  9 15 11  7 12 13  6  5  3 16  2 10 14 

  1  4  8  9 11 15  7 12 13  6  5  3 16  2 10 14 

  1  4  7  8  9 11 15 12 13  6  5  3 16  2 10 14 

  1  4  7  8  9 11 12 15 13  6  5  3 16  2 10 14 

  1  4  7  8  9 11 12 13 15  6  5  3 16  2 10 14 

  1  4  6  7  8  9 11 12 13 15  5  3 16  2 10 14 

  1  4  5  6  7  8  9 11 12 13 15  3 16  2 10 14 

  1  3  4  5  6  7  8  9 11 12 13 15 16  2 10 14 

  1  3  4  5  6  7  8  9 11 12 13 15 16  2 10 14 

  1  2  3  4  5  6  7  8  9 11 12 13 15 16 10 14 

  1  2  3  4  5  6  7  8  9 10 11 12 13 15 16 14 

  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 

下面是使用链表的直接插入排序算法：

#include <iostream>

using namespace std;

struct List
{
    int data;
    struct List *next;
} ;

void printList(struct List *head)
{
    struct List* ptr = head;
    while(ptr) {
        cout << ptr->data << " " ;
        ptr = ptr->next;
    }
    cout << endl;
}

struct List* createList(int a[], int sz)
{
    struct List *head = new struct List;
    struct List *current = head;

    for(int i = 0; i < sz; i++) {
        current->data = a[i];
        if (i == sz - 1 ) {
            current->next = NULL;
            break;
        }
        current->next = new struct List;
        current = current->next;
    }

    return head;
}

struct List* insertion(struct List *head)
  {
      if(head == 0) return head;

      // unsorted list - from the 2nd element
      struct List *unsorted = head->next;
      while(unsorted != 0)
      {
          // take key as an element in the unsorted list.
          struct List *prev = 0;
          struct List *iter = head;
          struct List *key = unsorted;

          // iterate within the sorted list and find the position
          while(iter != 0)
          {
              if(iter->data < key->data)
              {
                  prev = iter;
                  iter = iter->next;
              }
               else
                  break;
          }
          unsorted = unsorted->next;
          // if reached the end of sorted list 
          if(iter == key) 
              continue;

          // note down the position to replace in a sorted list
          struct List *replace = iter;

          //move iter to end of the sorted list 
          while(iter->next != key) iter=iter->next;

          // link to the upsorted list
          iter->next = unsorted;

          // delete the key and replace it in sorted list
          if(prev == 0) {
              head = key;
          } else {
                prev->next = key;
          }
          key->next = replace;
          printList(head);
       }
       return head;
  }

int main()
{
    int a[] = { 15, 9, 8, 1, 4, 11, 7, 12, 13, 6, 5, 3, 16, 2, 10, 14};
    int size = sizeof(a)/sizeof(int);

    struct List *head = createList(a, size);
    printList(head);
    head = insertion(head);
    printList(head);

    cout << endl;
    return 0;
}