DRML(CVPR 2016)Pytorch复现

参考

文献原文: Deep Region and Multi-label Learning for Facial Action Unit Detection

原文提供的代码：DRML

Pytorch版本参考代码：DRML_Pytorch

复现过程参考： DRML复现

代码结构组织设计参考： ME-GraphAU

实验设定

数据集：

名字：DISFA+.

简介：一共有九个人的面部数据。每张图有12个AUs，每个AU的值在于[0, 5]的整数表示其强度。 取前面七个同时作为训练集，最后两个人的数据作为测试集。

训练集的数量：42929 

测试集的数量：14739 

标签：{-1, 1}, 所有AU值小于2的为-1， 剩下的标签为1

图片输入大小：170X170X3

loss：multi-label sigmoid cross-entropy loss, L（true， prediction）

 

 

 

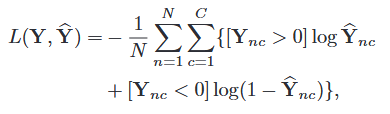
超参数和参数：

optimizer：SGD

learning rate：0.001

weight decay：0.005

momentum：0.9

epoch：20

batch size：64

 

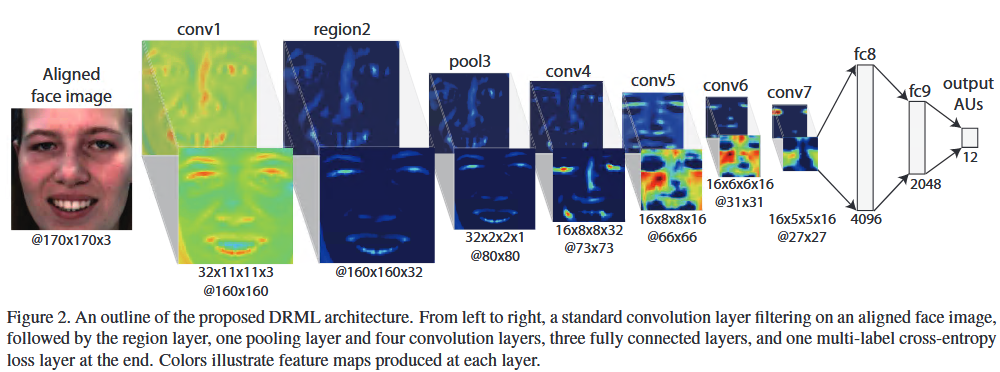
网络结构

论文中关于网络结构没有讲到的是，每个卷积层之后其实要加ReLU. 全连接层也有Dropout。具体实现看代码。

 

 

 

 

 

结论

在没有数据增强的情况下，得到的结果还可以的， 平均值为62.42%。 

 表中的结果分别是 F1-score/Accuracy

Model

AU1

AU2

AU4

AU5

AU6

AU9

AU12

AU15

AU17

AU20

AU25

AU26

mean

DRML标签为{-1, 1}

68.92/90.36

72.59/92.72

60.95/92.70

64.91/84.80

69.52/92.71

62.61/96.70

85.82/96.79

43.78/95.61

25.99/94.09

22.48/96.91

94.92/97.88

76.50/94.14

62.42/93.79

DRML标签为{0, 1}

68.93/90.37

72.60/92.73

60.95/92.71

64.91/84.81

69.52/92.71

62.62/96.70

85.83/96.80

43.79/95.61

26.00/94.09

22.49/96.61

94.92/97.89

76.50/94.14

62.42/93.79

 然后通过测验发现，在同样设定的情况下， 把标签{-1, 1} 改成 {0, 1} 的情况下， 两个标签的结果基本上是一样的。 另外为什么要有0和-1这两个标签呢？实际上是因为用来均衡样本不均衡的方法，把标签改为0可以忽视其存在，让标签1和-1的样本数量之间更为均衡。

 之后我拿CK+来测验模型是否真的有学到特征，我把CK+中每个文件夹中的图片拿最后一张作为输入，并且也对面部图片进行了面部裁剪。 对于标签，只要该AU出现在标签中，即使其强度为0 也被视为激活。 一共有593张图片来用于测试之前训练好的模型， 但是结果不怎么样，平均值只到21.47%。

 

 

Model

AU1

AU2

AU4

AU5

AU6

AU9

AU12

AU15

AU17

AU20

AU25

AU26

mean

DRML标签为{-1, 1}，CK+ test

11.11/62.23

6.02/73.69

50.27/52.92

37.82/67.28

40.88/45.36

14.20/51.10

8.33/77.74

0.00/81.11

19.96/39.12

4.55/85.83

48.80/42.66

15.74/56.66

21.47/61.31

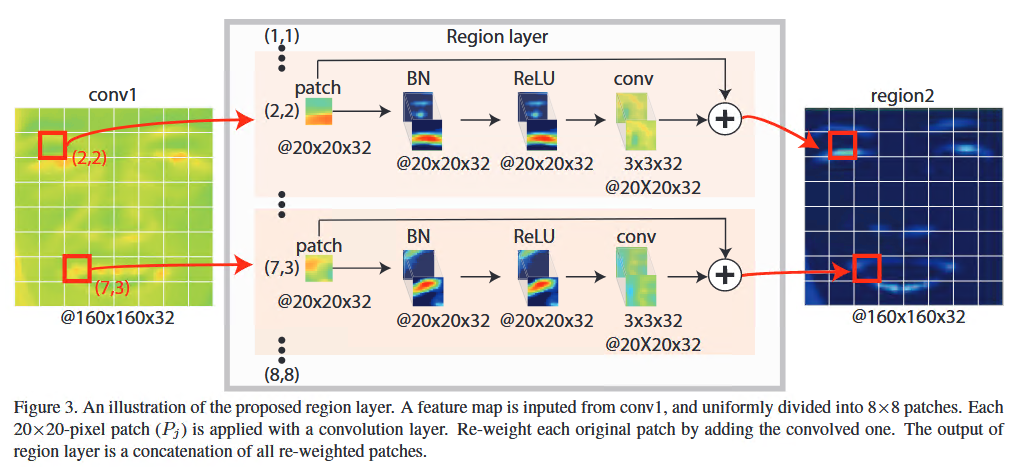
 我还测试了去掉Region Layer的网络架构，结果显示在训练当中，每个epoch的值都是非常类似的，不收敛，而所有AU的F1-score值都等于0。 由此可见，Region layer的层的必要性。

代码

GitHub: https://github.com/YIUYA/DRML

踩坑记录

 DRML的文献中使用的是该文作者自己设计的叫做multi-label sigmoid cross-entropy loss。其具体定义为以下：

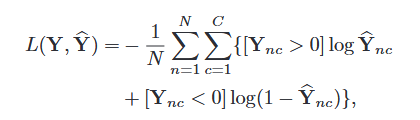
其中y是真实的标签， ŷ是预测的标签。C是AUs的总数，N是总样本数量。

文中说有三个标签{-1, 0, 1}, 然后根据loss的理解，作为标签为0的数据其实跟loss无关。loss只关注标签为1和-1的样本。 

另外我最开始理解错了loss， 我以为是 {1*[y > 0] * Log ŷ + (-1)*[y<0] * Log(1 -  ŷ)}， 通过该方法作为loss计算，我发现每个epoch的验证结果都是一模一样的，而且loss根本就没有收敛，一直在一个范围内来回摇摆。正确理解的是 {[y > 0]*Log ŷ +[y<0]* Log(1 -  ŷ)}, [y > 0] 和[y < 0]要么返回1要么返回0. 

还有一个就是计算 Log的时候要小心里面的值不要等于0或是小于0. 由于是sigmoid处理之后的值，所有输出值得范围是介于0和1之间。因此把所有输出等于0的值变成1e-20可以避免在原本的计算中梯度炸掉的坑。