BP神经网络中参考资料和相关概念理解
1.似然和概率的区别.
https://blog.csdn.net/qq_36396104/article/details/78171600
似然与概率
在统计学中,似然函数(likelihood function,通常简写为likelihood,似然)是一个非常重要的内容,在非正式场合似然和概率(Probability)几乎是一对同义词,但是在统计学中似然和概率却是两个不同的概念。概率是在特定环境下某件事情发生的可能性,也就是结果没有产生之前依据环境所对应的参数来预测某件事情发生的可能性,比如抛硬币,抛之前我们不知道最后是哪一面朝上,但是根据硬币的性质我们可以推测任何一面朝上的可能性均为50%,这个概率只有在抛硬币之前才是有意义的,抛完硬币后的结果便是确定的;而似然刚好相反,是在确定的结果下去推测产生这个结果的可能环境(参数),还是抛硬币的例子,假设我们随机抛掷一枚硬币1,000次,结果500次人头朝上,500次数字朝上(实际情况一般不会这么理想,这里只是举个例子),我们很容易判断这是一枚标准的硬币,两面朝上的概率均为50%,这个过程就是我们根据结果来判断这个事情本身的性质(参数),也就是似然。
结果和参数相互对应的时候,似然和概率在数值上是相等的,如果用 θ 表示环境对应的参数,x 表示结果,那么概率可以表示为:
P(x|θ)
P(x|θ)
是条件概率的表示方法,θ是前置条件,理解为在θ 的前提下,事件 x 发生的概率,相对应的似然可以表示为:
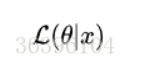
理解为已知结果为 x ,参数为θ (似然函数里θ 是变量,这里## 标题 ##说的参数是相对与概率而言的)对应的概率,即:
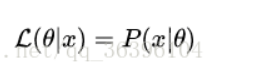
需要说明的是两者在数值上相等,但是意义并不相同,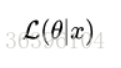
是关于 θ 的函数,而 P 则是关于 x 的函数,两者从不同的角度描述一件事情。
似然与概率举例
https://blog.csdn.net/songyu0120/article/details/85059149
有一个硬币,它有θ 的概率会正面向上,有1 − θ 的概率反面向上。θ是存在的,但是你不知道它是多少。
为了获得θ的值,你做了一个实验:将硬币抛10次,得到了一个正反序列:x = H H T T H T H H H H x=HHTTHTHHHHx=HHTTHTHHHH。无论θ 的值是多少,这个序列的概率值为 θ ⋅ θ ⋅ ( 1 − θ ) ⋅ ( 1 − θ ) ⋅ θ ⋅ ( 1 − θ ) ⋅ θ ⋅ θ ⋅ θ ⋅ θ = θ 7 ( 1 − θ ) 3。比如,如果θ 值为0,则得到这个序列的概率值为0。如果θ 值为1/2,概率值为1/1024。但是,我们应该得到一个更大的概率值,所以我们尝试了所有θ可取的值,画出了下图:
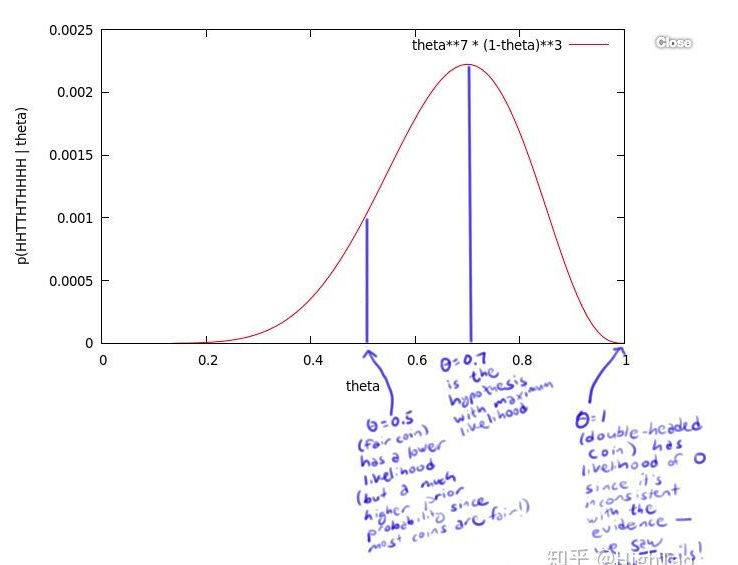
这个曲线就是θ的似然函数,通过了解在某一假设下,已知数据发生的可能性,来评价哪一个假设更接近θ的真实值。
如图所示,最有可能的假设是在θ=0.7的时候取到。但是,你无须得出最终的结论θ=0.7。事实上,根据贝叶斯法则,0.7是一个不太可能的取值(如果你知道几乎所有的硬币都是均质的,那么这个实验并没有提供足够的证据来说服你,它是均质的)。但是,0.7却是最大似然估计的取值。因为这里仅仅试验了一次,得到的样本太少,所以最终求出的最大似然值偏差较大,如果经过多次试验,扩充样本空间,
则最终求得的最大似然估计将接近真实值0.5。
2.交叉熵的概念
https://blog.csdn.net/b1055077005/article/details/100152102
交叉熵简介
交叉熵是信息论中的一个重要概念,主要用于度量两个概率分布间的差异性,要理解交叉熵,需要先了解下面几个概念。
信息量
信息奠基人香农(Shannon)认为“信息是用来消除随机不确定性的东西”,也就是说衡量信息量的大小就是看这个信息消除不确定性的程度。
“太阳从东边升起”,这条信息并没有减少不确定性,因为太阳肯定是从东边升起的,这是一句废话,信息量为0。
”2018年中国队成功进入世界杯“,从直觉上来看,这句话具有很大的信息量。因为中国队进入世界杯的不确定性因素很大,而这句话消除了进入世界杯的不确定性,所以按照定义,这句话的信息量很大。
根据上述可总结如下:信息量的大小与信息发生的概率成反比。概率越大,信息量越小。概率越小,信息量越大。
设某一事件发生的概率为P(x),其信息量表示为:
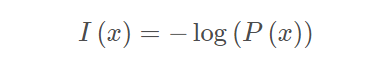
其中I(x)表示信息量,这里log表示以e为底的自然对数。
3.BP神经网络(梯度下降数学原理+反向传播原理)
https://zhuanlan.zhihu.com/p/65987457 梯度下降法和牛顿法
https://www.cnblogs.com/xiongchang95/p/8526745.html 看懂这个例子BP算法基本就懂了
https://www.cnblogs.com/shine-lee/p/11715033.html 具体可以参考这篇文章
https://blog.csdn.net/hfutdog/article/details/81151006 —导数、偏导数、方向导数、梯度



 浙公网安备 33010602011771号
浙公网安备 33010602011771号