神经网络性能的提升
虽然之前已经大概介绍了关于神经网络的基本结构,但是对于神经网络来说,还有很多可以提升的地方,包括不限于:参数的初始化,正则化,检测方式,除了梯度下降以外的优化算法,超参的调试,批量标准化,和TensorFlow等等。下面我们依次来介绍。
参数的初始化
由于梯度消失/爆炸的原因,参数的初始化关系着神经网络模型性能的问题。常见的参数的初始化有以下几种:
- 0初始化
- 随机初始化
- He初始化
0初始化:
所谓0初始化就是将所有的参数都初始化为零,但是由于初始化的值是一样的,它将不能破坏对称,以至于所有同源的参数的值将永远一样。
参数对称性
具有相同激活函数的两个隐藏单元连接到相同单元,那么这些单元必须具有不同的初始参数。一旦他们具有相同的初始参数,然后应用到确定性损失和模型的确定性学习算法将一直以相同的方式更新这两个单元。
随机初始化:
为了破坏对称,我们可以用随机初始化参数。但是随机初始化同样会陷入梯度消失/爆炸的问题,使得学习速率很慢或使得模型准确率下降。
梯度消失/爆炸:
那么什么是梯度消失和梯度爆炸呢?
![]() Fig. 1 梯度消失示意图
Fig. 1 梯度消失示意图
假设我们有一个很深的神经网络结构,如图Fig.1:假设我们的激励函数是线性的,如$g^{[l]}(z)=z$,且$W^{[l]}=\left[\begin{array}{cc} \frac{1}{2} &0\\0 &\frac{1}{2} \end{array}\right]$,那么我们可以得出:
$\hat{y} = W^{[L]}\left[\begin{array}{cc} \frac{1}{2} &0 \\ 0 &\frac{1}{2} \end{array}\right]^{[L-1]}X \tag{1}$
由以上公式我们可以看出$\hat{y}$是趋近于0的,假如$W^{[l]}
![]() Fig. 2 拟合状态
在欠拟合状态中,由于系统过于简单,使得系统的偏值(bias)很大,导致无论是训练集误差,还是测试集误差都很大。而在过度拟合状态中,又是由于系统过于复杂,使得系统的方差(variance)很大,导致虽然训练集的误差小,但是测试集的误差还是很大。因此,如何平衡系统的复杂程度,使得系统的效果达到最好呢?这时候就用到了L2正则化和Dropout了
#####L2正则化
我们在[神经网络的正向和反向传播](https://www.cnblogs.com/x1ao/p/12251998.html)中提及了Loss函数是:
$J = -\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} \tag{2}$
而L2正则化则是在Loss函数的基础上,增加了L2正则化项:
$J_{regularized} = \small \underbrace{-\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} }_\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W_{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{3}$
我们在成本函数可以看到,当参数值增大的时候成本函数会增加,因此可以用L2正则化来同时限制参数的大小,并且使得模型正确。但是由于成本函数的改变,在计算导数的时候也需要增加L2正则化的项。
#####Dropout
Dropout是正则化的一种方式,由名字退出(drop out)可以看出,它是以随机除去神经元来使得减少某个神经元的依赖程度,达到可以使用正则化的方式。在应用过程中,我们设置一个新的变量$D^{[l]} = \left[ d^{[l](1)}\, ... \,d^{[l](m)}\right]$用以表示第$l$个隐藏层的$D$,其中每一个$d^{(i)}$表示在第$i$个数据下的$d$,而$d$表示的是该神经元是否隐藏。因此它将是一个由$0$和$1$组成的向量。使用$d^{[l](i)} = np.random.rand(a^{[l](i)}.shape)梯度检查
Fig. 2 拟合状态
在欠拟合状态中,由于系统过于简单,使得系统的偏值(bias)很大,导致无论是训练集误差,还是测试集误差都很大。而在过度拟合状态中,又是由于系统过于复杂,使得系统的方差(variance)很大,导致虽然训练集的误差小,但是测试集的误差还是很大。因此,如何平衡系统的复杂程度,使得系统的效果达到最好呢?这时候就用到了L2正则化和Dropout了
#####L2正则化
我们在[神经网络的正向和反向传播](https://www.cnblogs.com/x1ao/p/12251998.html)中提及了Loss函数是:
$J = -\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L](i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} \tag{2}$
而L2正则化则是在Loss函数的基础上,增加了L2正则化项:
$J_{regularized} = \small \underbrace{-\frac{1}{m} \sum\limits_{i = 1}^{m} \large{(}\small y^{(i)}\log\left(a^{[L] (i)}\right) + (1-y^{(i)})\log\left(1- a^{[L](i)}\right) \large{)} }_\text{cross-entropy cost} + \underbrace{\frac{1}{m} \frac{\lambda}{2} \sum\limits_l\sum\limits_k\sum\limits_j W_{k,j}^{[l]2} }_\text{L2 regularization cost} \tag{3}$
我们在成本函数可以看到,当参数值增大的时候成本函数会增加,因此可以用L2正则化来同时限制参数的大小,并且使得模型正确。但是由于成本函数的改变,在计算导数的时候也需要增加L2正则化的项。
#####Dropout
Dropout是正则化的一种方式,由名字退出(drop out)可以看出,它是以随机除去神经元来使得减少某个神经元的依赖程度,达到可以使用正则化的方式。在应用过程中,我们设置一个新的变量$D^{[l]} = \left[ d^{[l](1)}\, ... \,d^{[l](m)}\right]$用以表示第$l$个隐藏层的$D$,其中每一个$d^{(i)}$表示在第$i$个数据下的$d$,而$d$表示的是该神经元是否隐藏。因此它将是一个由$0$和$1$组成的向量。使用$d^{[l](i)} = np.random.rand(a^{[l](i)}.shape)梯度检查
梯度检查是在检测Bug的过程中查看反向传播是否有错误的方法。使用公式:
$\frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{4}$
来进行梯度检查。
$difference = \frac {\mid\mid grad - gradapprox \mid\mid_2}{\mid\mid grad \mid\mid_2 + \mid\mid gradapprox \mid\mid_2}\tag{5}$
$gradapprox = \frac{J^+-J^-}{2\varepsilon}$
当$difference <10^{-7}$时,我们说梯度计算是正确的。
优化算法
Mini-batch
Mini-batch概念简介
Mini-batch梯度下降是相对于Batch梯度下降的一种优化。我们知道,在深度学习网络里,为了使得减少循环,我们使用了矢量化来加速。但是我们在每一次梯度下降的时候,必须使用所有的数据集吗?我们知道,有时候一个数据集是很大的,可能是百万级的,即使使用了矢量化来进行加速,那它一次梯度下降的运算量和运算时间也是很大的,导致了我们训练时间很长。反过头来,如果我们每次使用一部分数据集来进行梯度下降,那么不就解决了吗?
![]() Fig. 3 梯度下降
我们可以在Fig. 3中看到,蓝色是Batch梯度下降,在Batch中,每一次下降的方向一定是全局最优的;紫色是随机梯度下降,每次梯度下降都是使用一个数据进行梯度的计算,这使得它会有很大的噪声,最后收敛的区域也不如梯度下降;绿的的是Mini-batch梯度下降,收敛速度和噪声都介于随机梯度下降和Batch梯度下降之间,使用Mini-batch的好处是,可以使用矢量化的加速效果,又可以使得全局收敛的速度比较快。
那么如何选择Mini-batch的大小呢?
- 一般如果训练集的数目小于2000,我们直接使用Batch梯度下降
- 一般mini-batch的大小为2的倍数,且在64($2^6$)和256($2^9$)之间。
- 需要确保,mini-batch的每个数据集即($X^{\{t\}},Y^{\{t\}}$)不会超出CPU/GPU的储存大小
Fig. 3 梯度下降
我们可以在Fig. 3中看到,蓝色是Batch梯度下降,在Batch中,每一次下降的方向一定是全局最优的;紫色是随机梯度下降,每次梯度下降都是使用一个数据进行梯度的计算,这使得它会有很大的噪声,最后收敛的区域也不如梯度下降;绿的的是Mini-batch梯度下降,收敛速度和噪声都介于随机梯度下降和Batch梯度下降之间,使用Mini-batch的好处是,可以使用矢量化的加速效果,又可以使得全局收敛的速度比较快。
那么如何选择Mini-batch的大小呢?
- 一般如果训练集的数目小于2000,我们直接使用Batch梯度下降
- 一般mini-batch的大小为2的倍数,且在64($2^6$)和256($2^9$)之间。
- 需要确保,mini-batch的每个数据集即($X^{\{t\}},Y^{\{t\}}$)不会超出CPU/GPU的储存大小
Mini-batch实践
以下为Mini-batch的伪代码:
for t = 1, ... , 5000{
//Forward_prop on X{T}
Z1 = W1X{t}+b1
A1 = g1(Z1)
...
AL = gL(ZL)//L = mini-batch size
//Compute cost:
J{t} = 1/L * sum(loss(y_hat,y)) + lambd/(2*L) * sum(norm(Wl)*norm(Wl))
//Backward_prop to compute gradiants wrt. J{t}
...
//Update parameters
Wl = Wl - a*dWl
bl = bl - a*dbl
}
以上代码为一个epoch的运算,每将整个训练集遍历一遍叫做一个epoch,我们还需将上述执行多次实现函数收敛到最小值。
指数权重平均
指数权重平均的学习是之后要学习的Momentum和RMSprop方法的基础。指数权重平均实际上是一种平均方式,公式如下:
$V_t = \beta V_{t-1} + (1 - \beta)\theta_t \tag{6}$
其中$\theta_t$表示当天数据,$V_0 = 0$,$V_t$计算的是$\approx\frac{1}{1-\beta}$的平均值。推导如下:
例如$\beta = 0.9, t=100$
$V_{100} = 0.9V_{99} + 0.1\theta_{100}$
$V_{99} = 0.9V_{98} + 0.1\theta_{99}$
...
因此如果将$V_{99}, V_{98},...$带入:
$V_{100} = 0.1\theta_{100} + 0.1\,0.9\theta_{99} + 0.1\,0.9^2\theta_{98} + ... + 0.1\,0.9^{99}\theta_{1}$
如果我们将数据与权重系数分开的话:
![]() Fig. 4 指数权重平均
我们可以看到,权重系数是一个形如指数的方程。而且我们已知$(1-\varepsilon)^{\frac{1}{\varepsilon}} \approx \frac{1}{e}\approx 0.35$此时权重过小,我们默认对结果无影响。而实际上,在我们的方程里 $\varepsilon \approx 1-\beta$ 。因此指数平均天数 $\approx \frac{1}{1-\beta}$。伪代码实施:
Fig. 4 指数权重平均
我们可以看到,权重系数是一个形如指数的方程。而且我们已知$(1-\varepsilon)^{\frac{1}{\varepsilon}} \approx \frac{1}{e}\approx 0.35$此时权重过小,我们默认对结果无影响。而实际上,在我们的方程里 $\varepsilon \approx 1-\beta$ 。因此指数平均天数 $\approx \frac{1}{1-\beta}$。伪代码实施:
vtheta = 0
Repeta{
Get next thetat
vtheta := beta * vtheta + (1-beta)thetat}
由伪代码可知,此方法一行即可完成,且每次只需保存一个值,占用空间资源小。但是指数权重平均还有一个问题在于初始值\(V_0 = 0\),因此最开始的几个值是远小于其真实平均值的,因此单独使用指数权重平均的时候可以使用\(\frac{V_t}{1-\beta^t} = \beta V_{t-1} + (1-\beta)\theta_t\)。
Momentum
在使用Mini-batch的时候,由于每次梯度下降使用的数据集不再是全部的数据集,因此算出的梯度可能并不再是全局最优解,而是针对此数据集的最优解。
![]() Fig. 5 梯度噪声
针对如何给这样的问题进行加速呢?我们可以看到在$y$方向的数值是会震荡的,但是沿$x$方向没有震荡。因此可以指数权重平均来计算前$\frac{1}{1-\beta}$个的平均数用此来进行加速。
$V_{dW} = \beta V_{dW} + (1-\beta)dW$
$V_{db} = \beta V_{db} + (1-\beta)db$
$dW := dW - \alpha V_{dW}$
$db := db - \alpha V_{db}$
Fig. 5 梯度噪声
针对如何给这样的问题进行加速呢?我们可以看到在$y$方向的数值是会震荡的,但是沿$x$方向没有震荡。因此可以指数权重平均来计算前$\frac{1}{1-\beta}$个的平均数用此来进行加速。
$V_{dW} = \beta V_{dW} + (1-\beta)dW$
$V_{db} = \beta V_{db} + (1-\beta)db$
$dW := dW - \alpha V_{dW}$
$db := db - \alpha V_{db}$
Momentum:
On iteration t:
Compute dW, db
Vdw = beta * Vdw + (1 - beta) * dW
Vdv = beta * Vdb + (1 - beta) * db
w = w - alpha * Vdw
b = b - alpha * Vdb
在某些文献中可以看到,作者使用\(V_{dW} = \beta V_{dW} + dW\),这是在方程都除以\(1-\beta\)进行简化。
RMSprop
RMSprop也是加速mini-batch算法的优化方法之一。我们将横纵坐标分别表示为\(W\)和\(b\),因此我们希望加速\(W\),而减少\(b\)。我们可以从图像看出,纵坐标的导数明显大于横坐标的导数,我们可以借此来进行优化:
$S_{dW} = \beta_2 S_{dW} + (1-\beta_2)dW^2$
$S_{db} = \beta_2 S_{db} + (1-\beta_2)db^2$
$w:=w-\alpha\frac{dW}{\sqrt{S_{dW}+\varepsilon}}$
$b:=b-\alpha\frac{db}{\sqrt{S_{db}+\varepsilon}}$
```python
Sdw = beta2 * Sdw + (1 - beta2) * dw * dw
Sdb = beta2 * Sdb + (1 - beta2) * db * db
w = w - alpha * dw / sqrt(Sdw + eps)
b = b - alpha * dw / sqrt(Sdb + eps)
```
增加$\varepsilon = 10^{-8}$项是为了防止分母为$0$
#####Adams(Adaptive moment Estimation) : Momentum + RMSprop
Adams是Momentum和RMSprop的组合:
$V^{correct}_{dW} = \frac{V_{dW}}{1-\beta_1^t}$
$V^{correct}_{db} = \frac{V_{db}}{1-\beta_1^t}$
$S^{correct}_{dW} = \frac{S_{dW}}{1-\beta_2^t}$
$S^{correct}_{db} = \frac{S_{db}}{1-\beta_2^t}$
$dW:=dW - \alpha\frac{V^{correct}_{dW}}{\sqrt{S^{correct}_{dW}} + \varepsilon}$
$db:=db - \alpha\frac{V^{correct}_{db}}{\sqrt{S^{correct}_{db}} + \varepsilon}$
以上含有的超参包括:
$\alpha$需要调
$\beta_1 = 0.9$
$\beta_2 = 0.99$
$\varepsilon = 10^{-8}$
#####学习速率下降
如果学习速率一直保持不变的话,那么在最后收敛的时候很难收敛到最小值:
![]() Fig. 6 学习速率下降
因此我们需要在学习的同时减少学习速率,常见的学习速率有:
$\alpha = \frac{1}{1 + decay\_rate * epoch\_num} * \alpha_0$
$\alpha = 0.95 ^{epoch\_num} * \alpha_0$
$alpha = \frac{k}{\sqrt{epoch\_num}} * \alpha_0$ or $\frac{k}{\sqrt{t}}*\alpha_0$
...
Fig. 6 学习速率下降
因此我们需要在学习的同时减少学习速率,常见的学习速率有:
$\alpha = \frac{1}{1 + decay\_rate * epoch\_num} * \alpha_0$
$\alpha = 0.95 ^{epoch\_num} * \alpha_0$
$alpha = \frac{k}{\sqrt{epoch\_num}} * \alpha_0$ or $\frac{k}{\sqrt{t}}*\alpha_0$
...
局部最优解问题
- 很难出现陷入局部最优解的情况,因为参数数量足够大
- 容易有平坦层问题,需要使用Adam进行加速
超参的调试
调试步骤
我们有很多超参和它的优先级:
- \(\alpha\)优先级1
- \(\beta\)优先级2
- \(\beta_1, \beta_2, \varepsilon\)
- \(\#layers\)
- \(\#hidden \,units\)优先级2
- \(learning\, rate \,decay\)优先级3
- \(mini-batch\, size\)优先级2
因此在调试各种参数的时候我们需要注意,不能使用网格化来一个个的调试参数:
![]() Fig. 7 参数网格
因为我们不知道两个参数直接优先级是否一致,并且取值范围是否一致。另一个需要注意的问题是选择合适的尺度去选择参数:
例如在选择隐藏层数和每层神经元数的时候,我们可以使用均值分布进行搜索,但是选择学习速率或者$momentum$参数$\beta$的时候需要对其指数进行均值分布来搜索。
在调试参数的时候,对于不同的模型和商业形式我们主要有两种方式分别是熊猫(Pandas)和鱼子酱(Caviar):前者是主要关注一个模型,在模型运行的期间去调试并且关注效果。另一个则是同时运行很多个模型,来比较不同参数的效果。
Fig. 7 参数网格
因为我们不知道两个参数直接优先级是否一致,并且取值范围是否一致。另一个需要注意的问题是选择合适的尺度去选择参数:
例如在选择隐藏层数和每层神经元数的时候,我们可以使用均值分布进行搜索,但是选择学习速率或者$momentum$参数$\beta$的时候需要对其指数进行均值分布来搜索。
在调试参数的时候,对于不同的模型和商业形式我们主要有两种方式分别是熊猫(Pandas)和鱼子酱(Caviar):前者是主要关注一个模型,在模型运行的期间去调试并且关注效果。另一个则是同时运行很多个模型,来比较不同参数的效果。
Batch Normalization(BN)
来自于输入的归一化
在输入的归一化时我们将\(x = \frac{x - \mu}{\sqrt{\sigma^2 + \varepsilon}}\),且\(\mu = \frac{1}{m}\sum_i x^{(i)}\),\(\sigma^2 = \frac{1}{m}\sum_i(x^{(i)} - \mu)^2\)
BN
我们在做BN的时候,也将每一个隐藏层的\(Z^{(i)}\)归一化:
$\mu = \frac{1}{m}\sum_i z^{(i)}$
$\sigma^2 = \frac{1}{m}\sum_i(z^{(i)} - \mu)^2$
$z^{(i)}_{norm} = \frac{z^{(i)} - \mu}{\sqrt{\sigma^2 + \varepsilon}}$
$\tilde{z^{(i)}} = \gamma z^{(i)}_{norm} + \beta$
因为$z^{(i)}_{norm}$是均值为0,方差为1的向量,但是有时候我们希望形成其它的均值和方差,因此我们引用了$\tilde{z^{(i)}}$.
#####实践到神经网络
for t = 1, ... ,num_minibatch
compute forward_prop on X{t}
In each hidden layer, replace Zl with tilde_ZL
Use back_prop compute: dWl, dbetal, dgammal
Update
#Notice that this also works on Momentum/RMSprop/Adam
原因:
- 使得每个隐藏层的参数独立
- 因为引入了噪声,有了轻微的正则化的效果
测试:
在测试阶段,我们仅有一个例子,如何得到合适的\(\mu\)和\(\sigma^2\)呢?
我们应该保存在训练时候得到的\(\mu^{\{t\}[l]}\)以及\(\sigma^{2\{t\}[l]}\)使用指数权重平均用来计算\(\mu\)和\(\sigma^2\)。
多种类分类
Softmax layer
当处理多种类分类问题的时候,我们需要输出层的激励函数可以输出\(\in R^{n^{[l]}\times 1}\)的结果,因此我们定义一个新的激励函数名字是softmax:
$g^{[L]} = \frac{e^{Z^{[L]}}}{\sum_i e^{Z^{[L]}}_i}$
并且定义新的损失方程(loss function):
$Loss = -\sum _{i}^C y_i log\hat{y}_i$
where $C = Num\_classes$
#####Hardmax
Hardmax是相对于softmax而言的,我们看到在softmax里,我们的结果是某一个概率,然而在hardmax里,我们粗暴的将$Z^{[L]}$最大的数定为$1$,而其它设为$0$.
 Fig. 1 梯度消失示意图
Fig. 1 梯度消失示意图
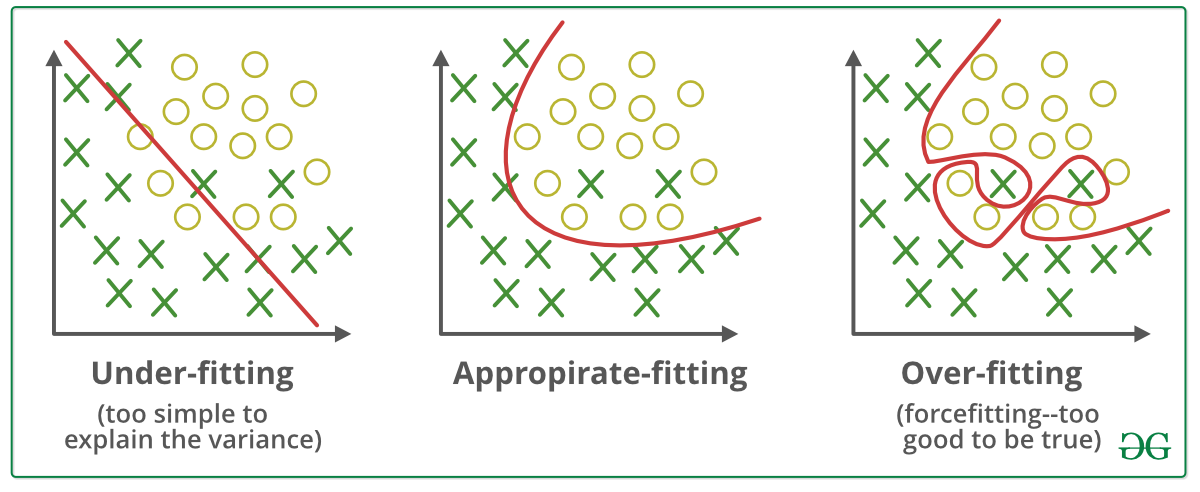 Fig. 2 拟合状态
在欠拟合状态中,由于系统过于简单,使得系统的偏值(bias)很大,导致无论是训练集误差,还是测试集误差都很大。而在过度拟合状态中,又是由于系统过于复杂,使得系统的方差(variance)很大,导致虽然训练集的误差小,但是测试集的误差还是很大。因此,如何平衡系统的复杂程度,使得系统的效果达到最好呢?这时候就用到了L2正则化和Dropout了
#####L2正则化
我们在[神经网络的正向和反向传播](https://www.cnblogs.com/x1ao/p/12251998.html)中提及了Loss函数是:
Fig. 2 拟合状态
在欠拟合状态中,由于系统过于简单,使得系统的偏值(bias)很大,导致无论是训练集误差,还是测试集误差都很大。而在过度拟合状态中,又是由于系统过于复杂,使得系统的方差(variance)很大,导致虽然训练集的误差小,但是测试集的误差还是很大。因此,如何平衡系统的复杂程度,使得系统的效果达到最好呢?这时候就用到了L2正则化和Dropout了
#####L2正则化
我们在[神经网络的正向和反向传播](https://www.cnblogs.com/x1ao/p/12251998.html)中提及了Loss函数是:
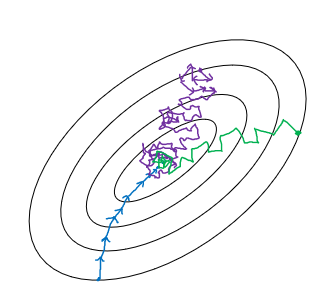 Fig. 3 梯度下降
Fig. 3 梯度下降
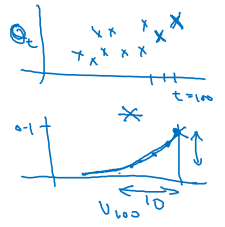 Fig. 4 指数权重平均
Fig. 4 指数权重平均
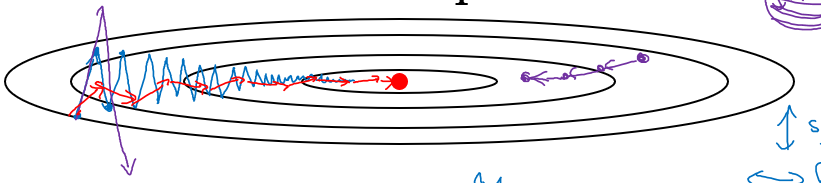 Fig. 5 梯度噪声
Fig. 5 梯度噪声
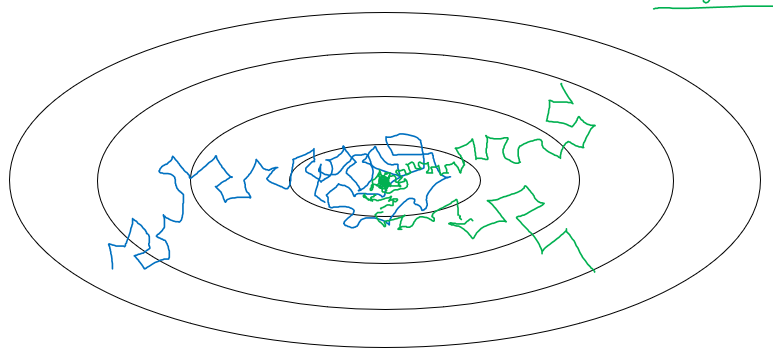 Fig. 6 学习速率下降
Fig. 6 学习速率下降
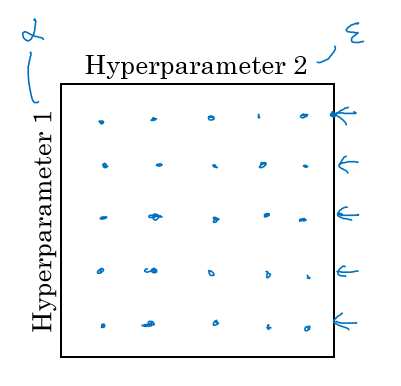 Fig. 7 参数网格
Fig. 7 参数网格




 浙公网安备 33010602011771号
浙公网安备 33010602011771号