04_AES算法原理
AES算法原理
一、AES简单介绍
1. AES算法特点
- 在一个分组长度内,明文的长度变化,AES的加密结果长度都一样
- 密钥长度128、192、256三种,如果少1个十六进制数,会在前面补0
- 分组长度为128比特位,也就是16字节
- 密文长度与填充后的明文长度有关,一般是16字节的倍数
2. Rijndael算法
Rijndael算法也叫AES算法,Rijndael算法本身分组长度可变,但是定为AES算法后,分组长度只有128一种
3. 运算单位
DES当中是针对比特位进行操作的,而AES中是针对字节进行操作的
4. 轮运算
AES128:10轮运算AES192:12轮运算AES256:14轮运算
二、AES原理
这里分析的是AES128的分组加密。
1. 明文处理
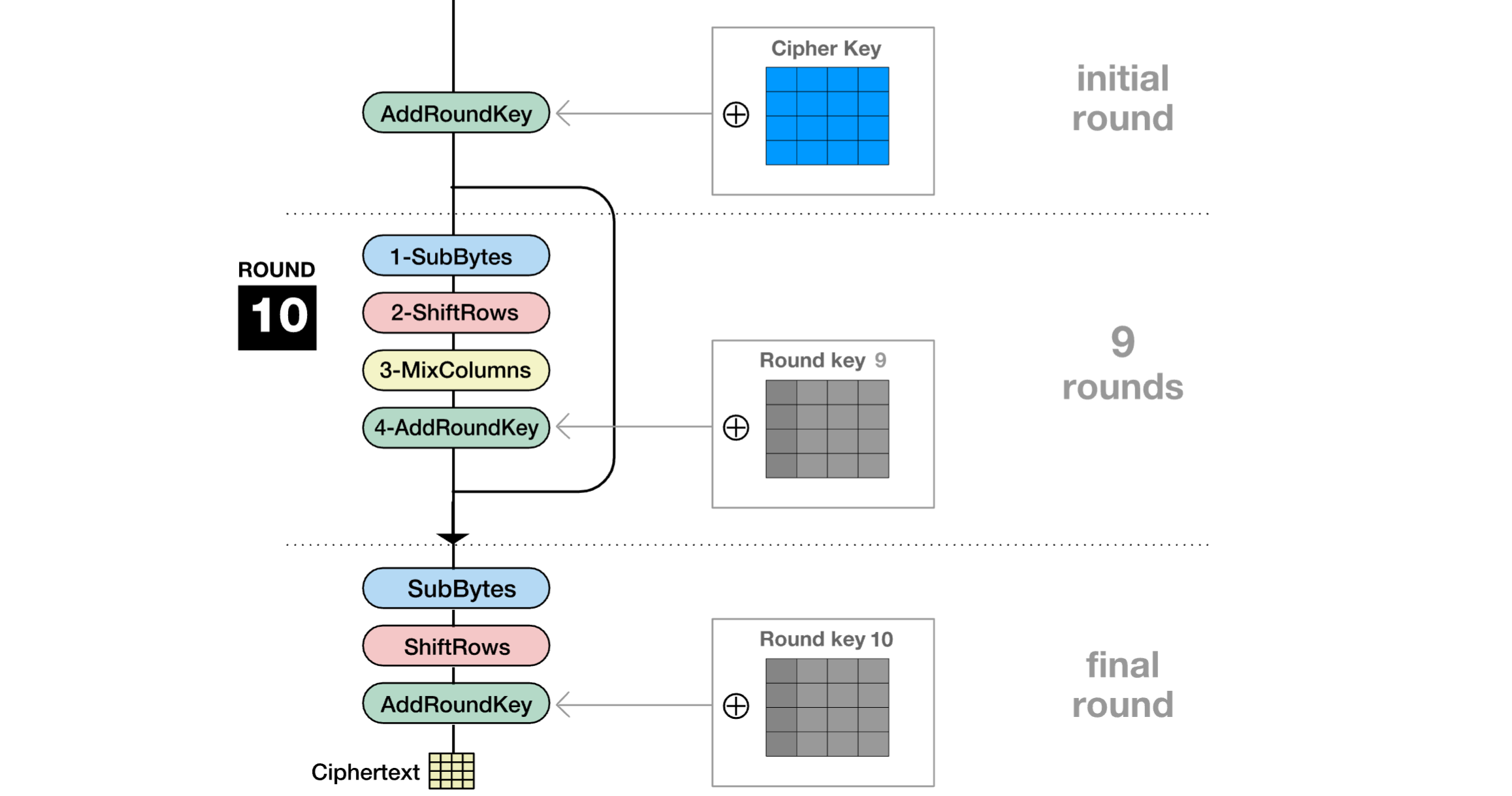
上图就是一个分组当中的轮运算,首先先与密钥进行一个\(\oplus\)异或运算,接着是9轮的循环运算,分别是SubBytes (字节代换),ShiftRows (行变换),MixColumns (列混合),AddRoundKey (轮密钥加\(\oplus\))。最后第十轮少了一个列混合,经过第十轮的运算之后Ciphertext(密文)。
下面来分析一下这个明文轮运算当中的一些运算的细节。
SubBytes (字节代换)
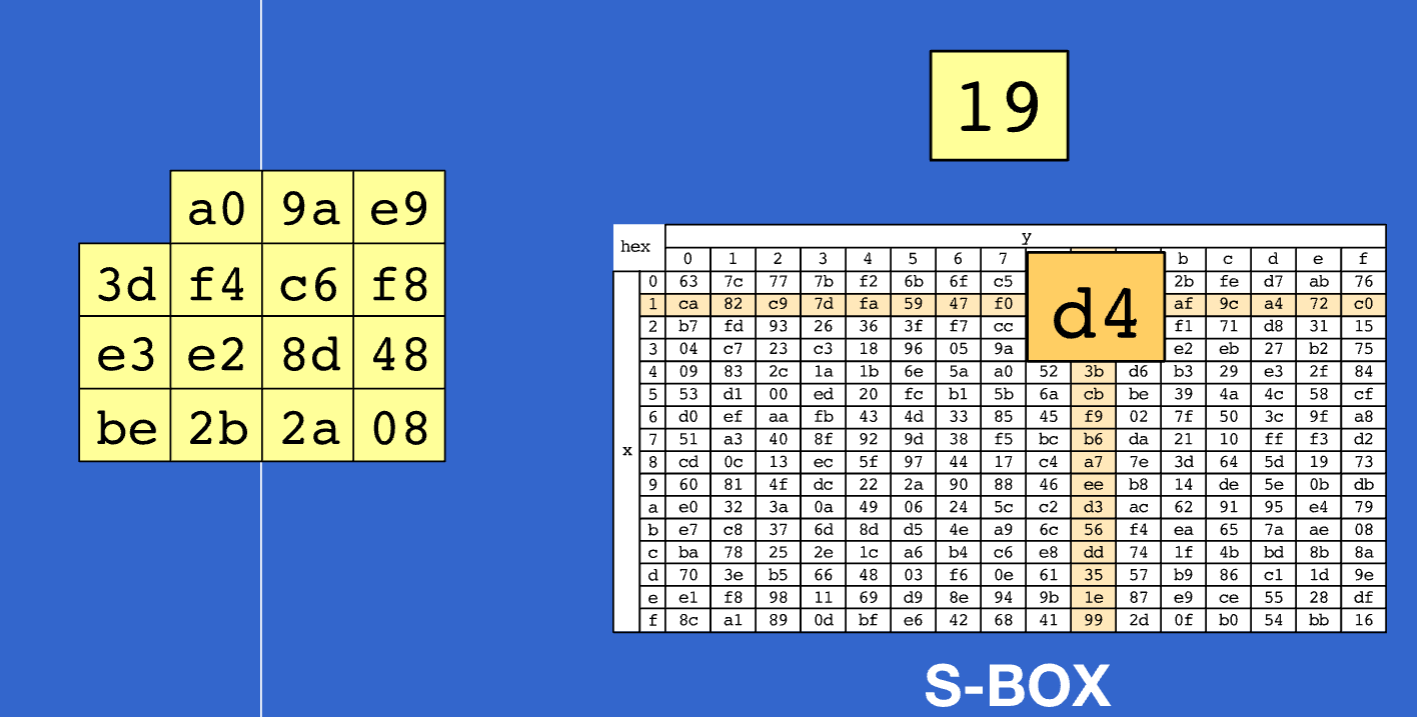
字节代换如上图所示,直接取出一个字节,然后高4bit作为s和的行索引,低四位作为s盒的列索引。取出对应S盒当中的数值然后替换。这一步非常的简单就是一个查表的过程,就不赘述了。
ShiftRows (行变换)
紧接着就是行变换了,行变换就是对每一行进行循环位移操作。具体来说就是:
- 第一行不变
- 第二行循环左移1位
- 第三行循环左移2位
- 第四行循环左移3位
整个变换过程如下图所示:
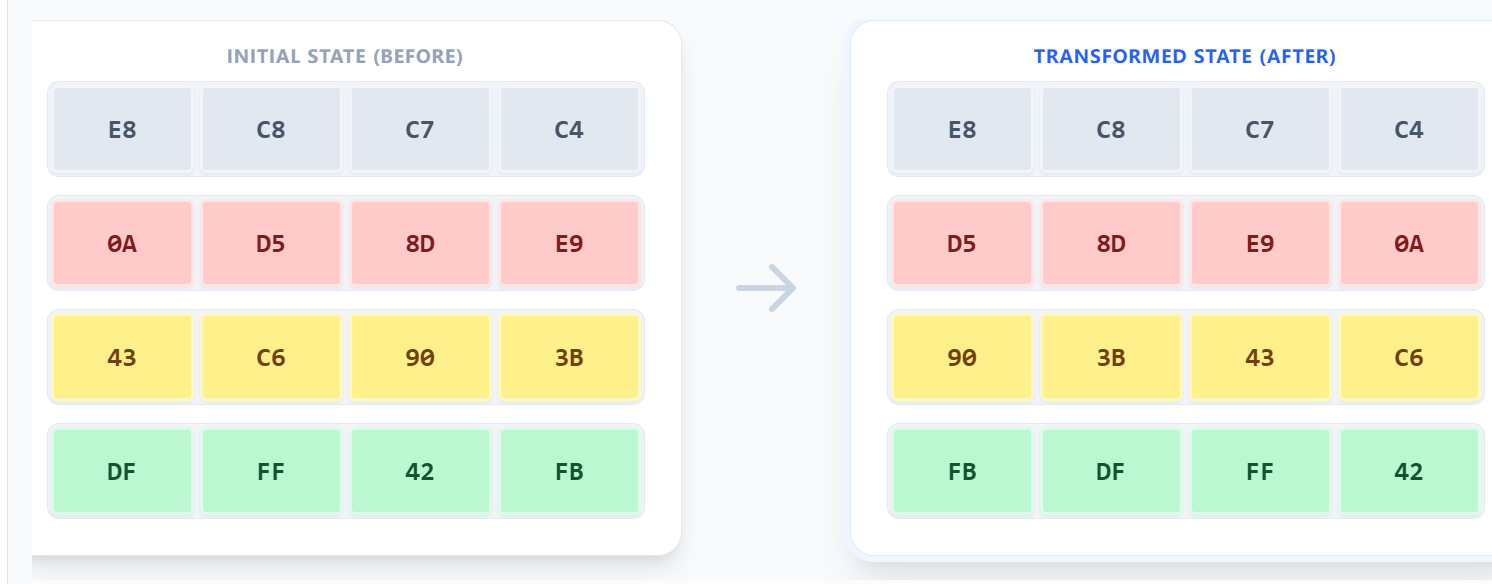
MixColumns (列混合)
列混淆是对矩阵每一列进行线性变化,通过矩阵乘法实现,步骤如下图:

要注意的是,这里的列变换,一旦矩阵乘法当中出现溢出就要\(\oplus 0x1B\) , 而这个矩阵乘法的运算也有点不同,使用了异或代替了乘法之后的加法,乘法当中也是使用多轮的异或而不是简单的加法。
AddRoundKey (轮密钥加\(\oplus\))
接着就是轮密钥异或了
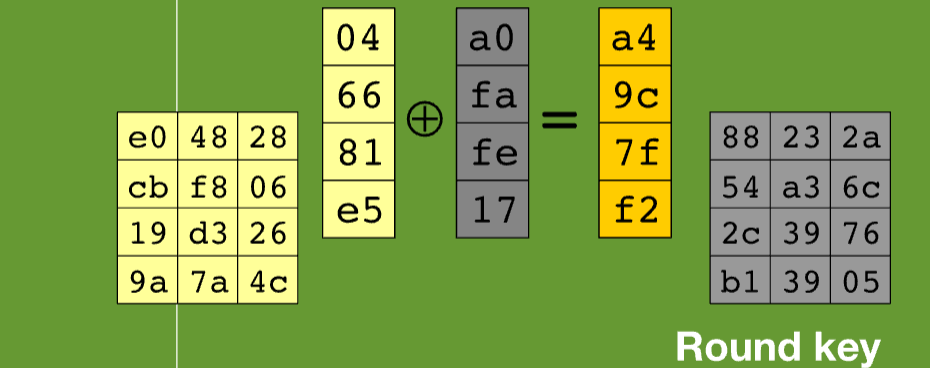
这个就是简单的异或,然后进行9轮轮运算,最后在进行第十轮运算就得出密文了
2. 子密钥生成
密钥扩展
传入16字节种子密钥初始化,得到\(W_0-W_3\)作为种子密钥,然后将种子密钥扩展得到剩下的\(W_4 - W_{43}\)。扩展的规则如下:
- 如果
i%4!=0,\(W_i = W_{i-1} \oplus W_{i-4}\) - 如果
i%4==0,则\(W_i = T(W_{i-1}) \oplus W_{i-4}\)
T函数流程:循环左移1个字节、s盒替换、与Rcon异或,如下图所示:
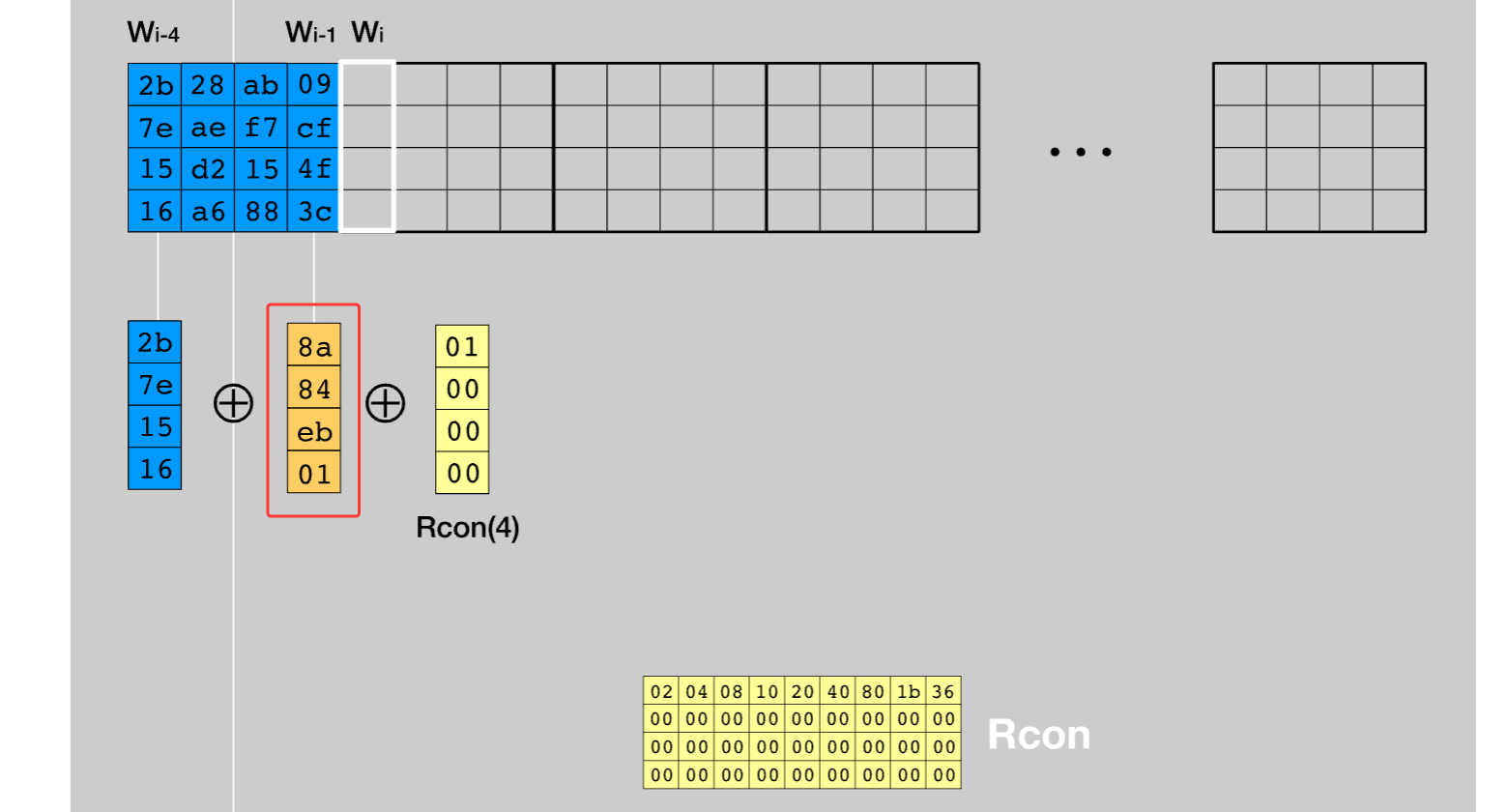
框选部分就是循环左移之后查表得出的值。接着与Rcon(i)进行异或。
最终可以得到44组密钥,然后每一轮的addRoundKey使用4组。
三、AES源码分析
这里大致分析一下各个工作部分的代码:
1. aesEncrypt
// 参数: 密钥,密钥长度, 明文, 密文,明文长度
int aesEncrypt(const uint8_t *key, uint32_t keyLen, const uint8_t *pt, uint8_t *ct, uint32_t len) {
AesKey aesKey;
uint8_t *pos = ct;
const uint32_t *rk = aesKey.eK; //解密密钥指针
uint8_t out[BLOCKSIZE] = {0};
uint8_t actualKey[16] = {0};
uint8_t state[4][4] = {0};
if (NULL == key || NULL == pt || NULL == ct) {
printf("param err.\n");
return -1;
}
if (keyLen > 16) {
printf("keyLen must be 16.\n");
return -1;
}
if (len % BLOCKSIZE) {
printf("inLen is invalid.\n");
return -1;
}
memcpy(actualKey, key, keyLen);
keyExpansion(actualKey, 16, &aesKey); // 秘钥扩展
for (int i = 0; i < len; i += BLOCKSIZE) { // 明文分
loadStateArray(state, pt); // 明文转成4 x 4矩阵
addRoundKey(state, rk); // 轮秘钥加
for (int j = 1; j < 10; ++j) {
rk += 4;
subBytes(state); // 字节替换
shiftRows(state); // 行移位
mixColumns(state); // 列混合
addRoundKey(state, rk); // 轮秘钥加
}
subBytes(state); // 字节替换
shiftRows(state); // 行移位
addRoundKey(state, rk + 4); // 轮秘钥加
storeStateArray(state, pos); // 矩阵转一维数组
pos += BLOCKSIZE; // 加密数据内存指针移动到下一个分组
pt += BLOCKSIZE; // 明文数据指针移动到下一个分组
rk = aesKey.eK; // 恢复rk指针到秘钥初始位置
}
return 0;
}
加密函数大致流程如上。
2. keyExpansion密钥扩展
int keyExpansion(const uint8_t *key, uint32_t keyLen, AesKey *aesKey) {
if (NULL == key || NULL == aesKey) {
printf("keyExpansion param is NULL\n");
return -1;
}
if (keyLen != 16) {
printf("keyExpansion keyLen = %d, Not support.\n", keyLen);
return -1;
}
uint32_t *w = aesKey->eK; //加密秘钥
uint32_t *v = aesKey->dK; //解密秘钥
for (int i = 0; i < 4; ++i) {
LOAD32H(w[i], key + 4 * i);
}
for (int i = 0; i < 10; ++i) {
w[4] = w[0] ^ MIX(w[3]) ^ rcon[i];
w[5] = w[1] ^ w[4];
w[6] = w[2] ^ w[5];
w[7] = w[3] ^ w[6];
w += 4;
}
w = aesKey->eK + 44 - 4;
for (int j = 0; j < 11; ++j) {
for (int i = 0; i < 4; ++i) {
v[i] = w[i];
}
w -= 4;
v += 4;
}
return 0;
}
首先通过LOAD32H将二维数组矩阵,当中的每一列取出,获取\(W_0-W_3\)。LOAD32H是一个宏,定义如下:
#define LOAD32H(x, y) \
do { (x) = ((uint32_t)((y)[0] & 0xff)<<24) | ((uint32_t)((y)[1] & 0xff)<<16) | \
((uint32_t)((y)[2] & 0xff)<<8) | ((uint32_t)((y)[3] & 0xff));} while(0)
就是将矩阵的每一列拼成一个DWORD的数值。
接着就是for循环10轮,搞定剩下的\(W_{4}\)~\(W_{43}\),注意这里面的循环迭代的是w指针,所以计算的索引不变,因为相对偏移不变。只要索引是4就要额外处理,MIX作用是先字节替换再循环左移,同样也是一个宏,具体定义如下:
#define MIX(x) (((S[BYTE(x, 2)] << 24) & 0xff000000) ^ ((S[BYTE(x, 1)] << 16) & 0xff0000) ^ \
((S[BYTE(x, 0)] << 8) & 0xff00) ^ (S[BYTE(x, 3)] & 0xff))
// 取从低位开始的第n个字节
#define BYTE(x, n) (((x) >> (8 * (n))) & 0xff)
最后就是给解密的扩展密钥赋值,解密时使用的就是加密密钥的逆序。
3. loadStateArray数组转矩阵
int loadStateArray(uint8_t (*state)[4], const uint8_t *in)
{
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[j][i] = *in++;
}
}
return 0;
}
就是一个简单的二维数组赋值。
4. addRoundKey轮密钥加
int addRoundKey(uint8_t (*state)[4], const uint32_t *key) {
uint8_t k[4][4];
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
k[i][j] = (uint8_t) BYTE(key[j], 3 - i);
state[i][j] ^= k[i][j];
}
}
return 0;
}
这里先使用BYTE将DWORD类型的key取出一个个对应的字节,然后再进行异或
5. subBytes字节替换
int subBytes(uint8_t (*state)[4]) {
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
state[i][j] = S[state[i][j]]; //直接使用原始字节作为S盒数据下标
}
}
return 0;
}
字节替换就直接使用了原始字节作为S盒数据的下标,这个方法与分开左右两边查表是等效的。
6. shiftRows行变换
int shiftRows(uint8_t (*state)[4]) {
uint32_t block[4] = {0};
for (int i = 0; i < 4; ++i) {
LOAD32H(block[i], state[i]); // 先拼成32bit数据
block[i] = ROF32(block[i], 8 * i);
STORE32H(block[i], state[i]);
}
return 0;
}
行变化先将数组的每一行拼成一个32bit的值,然后再进行循环左移i个字节,也就是\(8 \times i\)个比特位。然后使用STORE32存储回state当中。
7. mixColumns列混淆
int mixColumns(uint8_t (*state)[4]) {
uint8_t tmp[4][4];
uint8_t M[4][4] = {{0x02, 0x03, 0x01, 0x01},
{0x01, 0x02, 0x03, 0x01},
{0x01, 0x01, 0x02, 0x03},
{0x03, 0x01, 0x01, 0x02}};
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
tmp[i][j] = state[i][j];
}
}
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) { //伽罗华域加法和乘法
state[i][j] = GMul(M[i][0], tmp[0][j]) ^ GMul(M[i][1], tmp[1][j])
^ GMul(M[i][2], tmp[2][j]) ^ GMul(M[i][3], tmp[3][j]);
}
}
return 0;
}
这里就是进行的伽罗华域加法和乘法,然后GMul当中还有溢出检测:
uint8_t GMul(uint8_t u, uint8_t v) {
uint8_t p = 0;
for (int i = 0; i < 8; ++i) {
if (u & 0x01) {
p ^= v;
}
int flag = (v & 0x80);
v <<= 1;
if (flag) {
v ^= 0x1B; /* x^8 + x^4 + x^3 + x + 1 */
}
u >>= 1;
}
return p;
}
这里的矩阵乘法(伽罗华域加法和乘法),可以理解为,原来乘法就是多次加法,但是在这里面加法变成了异或,每轮循环要左移一位,如果溢出,则需要\(\oplus 0x1B\)
那么到这里大致AES整个过程了,这里只分析的是ECB模式下的,一个分组的加密过程。其他加密模式都可以在这个基础上推广。
四、查表法实现AES加密
AES每一轮当中有四层结构,加密过程分别是字节代换层(Byte Substitution Layer)、ShiftRows层、MixColumn层和密钥加法层(Key Addition Layer)。
S盒是一个有限集,而且是根据输入进行映射,S盒之后的矩阵计算,每个元素其实也有着一个映射关系,而对于查表法的实现就是对前三层操作的合并。
而在轮运算当中,字节代换和循环左移其实是可以交换顺序的。对于列混淆当中有如下的矩阵公式:
这里的B0就是经过字节代换循环左移之后的矩阵。然后根据矩阵的乘法可以将列向量拆开,变成这样:
那么上面的等式就能够继续推广成这样:
注意:这里的A0->A5是已经循环左移之后的排序。所以这三个步骤可以根据这个公式变成从\(A_0\)-->\(C_0\)的一个映射,也就能够使用查表来实现了。接着将这个查的表称为T盒,而加密过程总共有4个T表:
最终的轮操作可以化简成下面的公式:
接下来给出的实例代码是相邻两轮的操作,使用C/C++编写:
void aes_encrypt_rounds(uint32_t *wa, uint32_t *wb, const uint32_t *keys, int rounds) {
uint32_t wa0 = wa[0], wa1 = wa[1], wa2 = wa[2], wa3 = wa[3];
uint32_t wb0 = wb[0], wb1 = wb[1], wb2 = wb[2], wb3 = wb[3];
for (int i = 1; i < (rounds / 2); ++i) {
// --- 偶数轮 (Even-number rounds) ---
wa0 = TE0[wb0 >> 24] ^ TE1[(wb1 >> 16) & 0xFF] ^ TE2[(wb2 >> 8) & 0xFF] ^ TE3[wb3 & 0xFF] ^ keys[8 * i];
wa1 = TE0[wb1 >> 24] ^ TE1[(wb2 >> 16) & 0xFF] ^ TE2[(wb3 >> 8) & 0xFF] ^ TE3[wb0 & 0xFF] ^ keys[8 * i + 1];
wa2 = TE0[wb2 >> 24] ^ TE1[(wb3 >> 16) & 0xFF] ^ TE2[(wb0 >> 8) & 0xFF] ^ TE3[wb1 & 0xFF] ^ keys[8 * i + 2];
wa3 = TE0[wb3 >> 24] ^ TE1[(wb0 >> 16) & 0xFF] ^ TE2[(wb1 >> 8) & 0xFF] ^ TE3[wb2 & 0xFF] ^ keys[8 * i + 3];
// --- 奇数轮 (Odd-number rounds) ---
wb0 = TE0[wa0 >> 24] ^ TE1[(wa1 >> 16) & 0xFF] ^ TE2[(wa2 >> 8) & 0xFF] ^ TE3[wa3 & 0xFF] ^ keys[8 * i + 4];
wb1 = TE0[wa1 >> 24] ^ TE1[(wa2 >> 16) & 0xFF] ^ TE2[(wa3 >> 8) & 0xFF] ^ TE3[wa0 & 0xFF] ^ keys[8 * i + 5];
wb2 = TE0[wa2 >> 24] ^ TE1[(wa3 >> 16) & 0xFF] ^ TE2[(wa0 >> 8) & 0xFF] ^ TE3[wa1 & 0xFF] ^ keys[8 * i + 6];
wb3 = TE0[wa3 >> 24] ^ TE1[(wa0 >> 16) & 0xFF] ^ TE2[(wa1 >> 8) & 0xFF] ^ TE3[wa2 & 0xFF] ^ keys[8 * i + 7];
}
// 将结果写回指针 (如果需要在函数外使用)
wa[0] = wa0; wa[1] = wa1; wa[2] = wa2; wa[3] = wa3;
wb[0] = wb0; wb[1] = wb1; wb[2] = wb2; wb[3] = wb3;
}
但是要值得注意的是,最后一轮没有MixColumn操作,所以这一轮要额外使用S盒操作一下,不过在openssl当中,加密过程的S盒也融入了T表当中。有了加密过程解密过程也可以按照这种方式扩展了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号