最大子数组之和(二维矩形)
一、实验目的
1,以指定格式的文本文件形式输入数组。
2,数组由一维变为二维。
3,熟练使用git常用命令将作业签入代码版本控制平台。
4,给出单元测试/代码覆盖率的最终覆盖率的报告,撰写博客。
二、代码实现
"""本程序采用暴力破解的方法,将数据转换为二维数组后得出行数和列数,外层四个for循环规定矩形大小,内层两个for循环将矩形内的数据相加,最后将其存储到新数组中得到其最大值。 基本思想就是不断给出定固定矩形框然后往二维数组中挨个套,得到所以可能性,从而求出最大值""" import numpy as np # 读取并转换为二维数组 data = np.loadtxt(r"C:\Users\32762\Desktop\list.txt") # 二维数组行数 line = data.shape[0] # 二维数组列数 column = data.shape[1] # 定义一个列表存储矩形数据和 lst = [] for i in range(0, column): # 矩形框起始列 for m in range(i, column): # 矩形框终止列 for j in range(0, line): # 矩形框起始行 for n in range(j, line): # 矩形框终止行 t = 0 # 每次将t置为0,防止干扰 for q in range(j, n + 1): # 加一是由于range()包头不包尾,不能包含最后一行终止行 for o in range(i, m+1): if o <= column and q <= line: # 判断语句是防止越界 t = data[q][o] + t else: continue lst.append(t) print(lst) print(max(lst))
3、运行结果

数组中数据就是所有可能的矩形的和,25.0是其中的最大值
4、单元测试
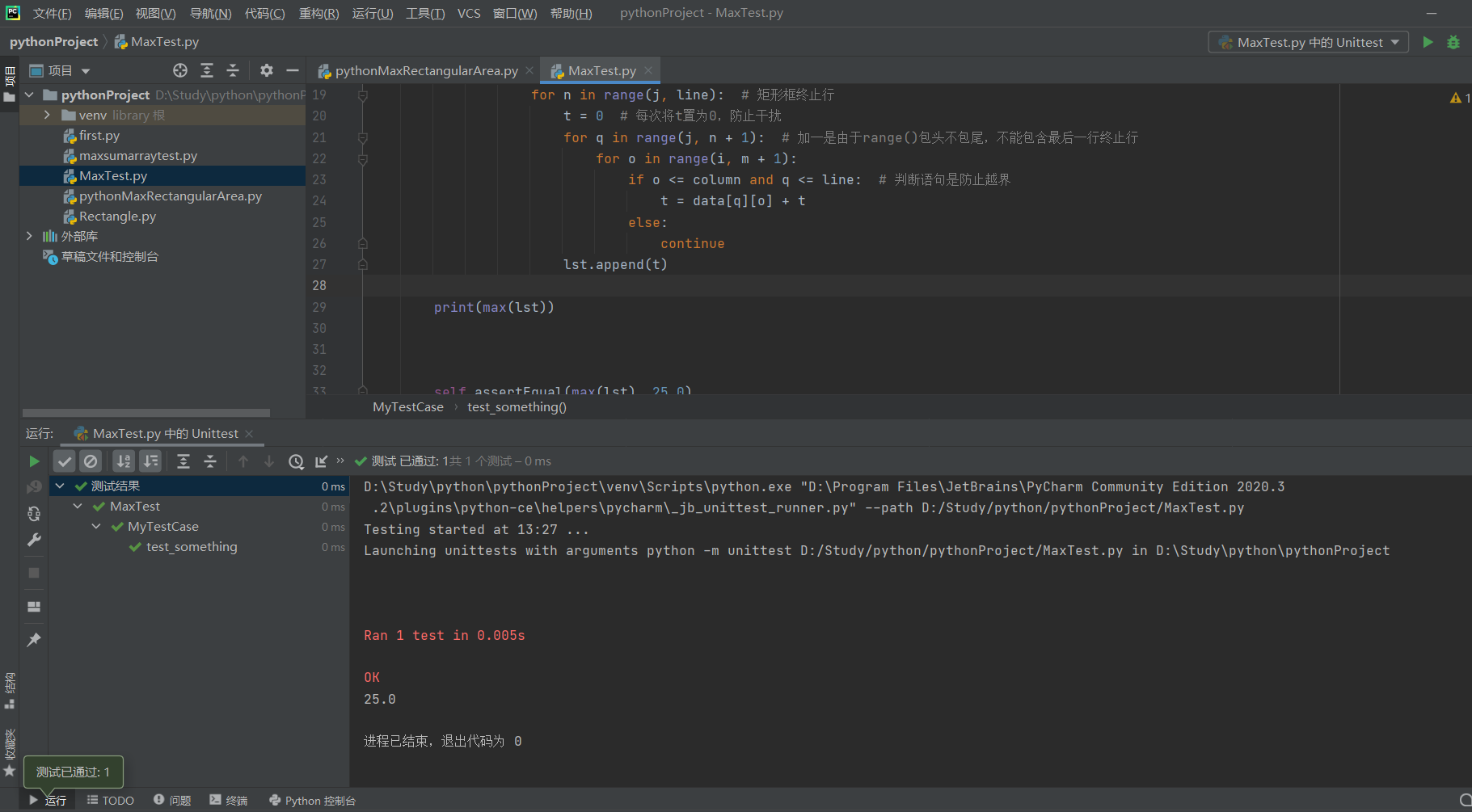
测试数据入下

5、覆盖率
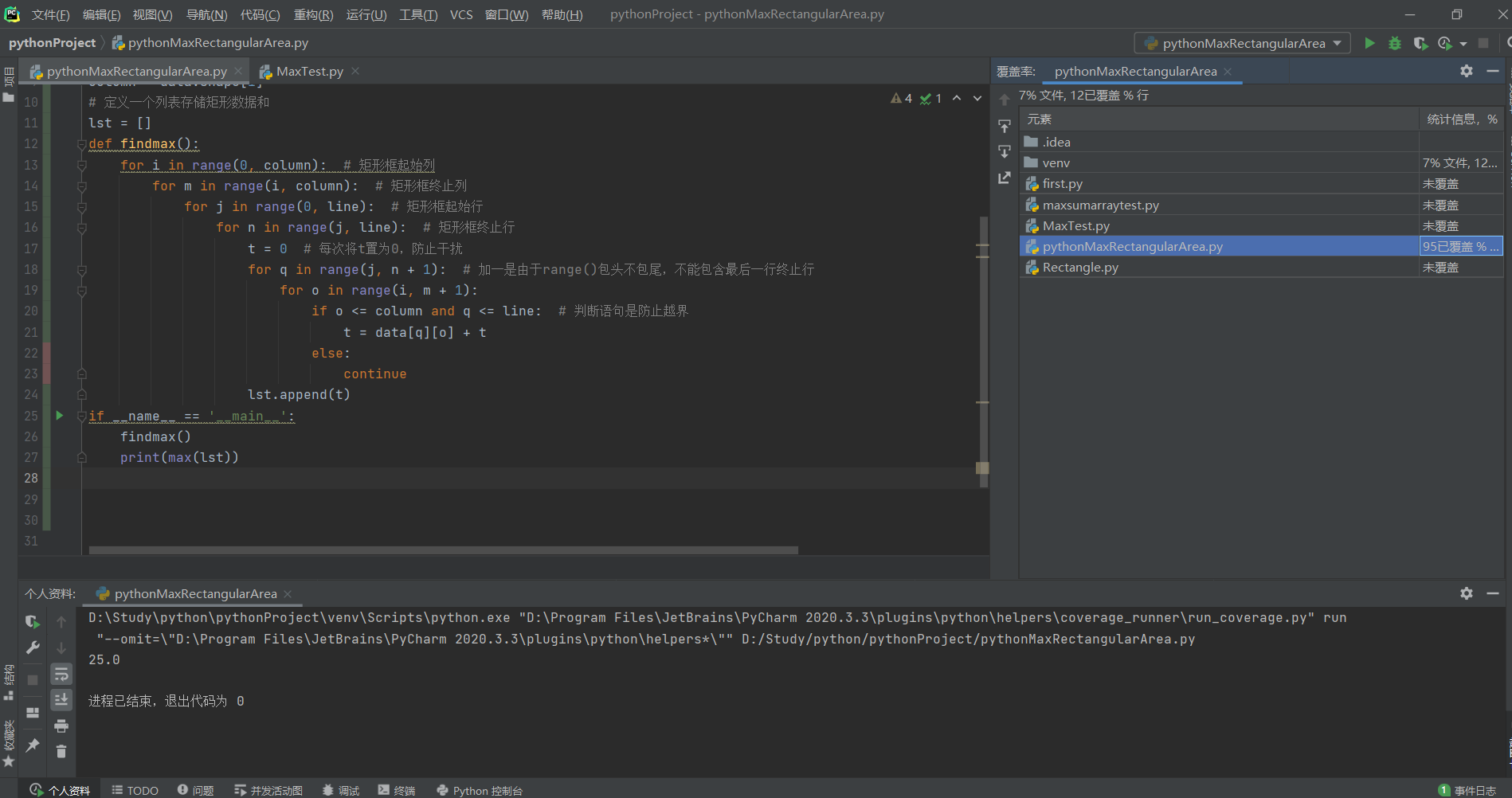
绿色部分表示已覆盖
6、简单性能分析
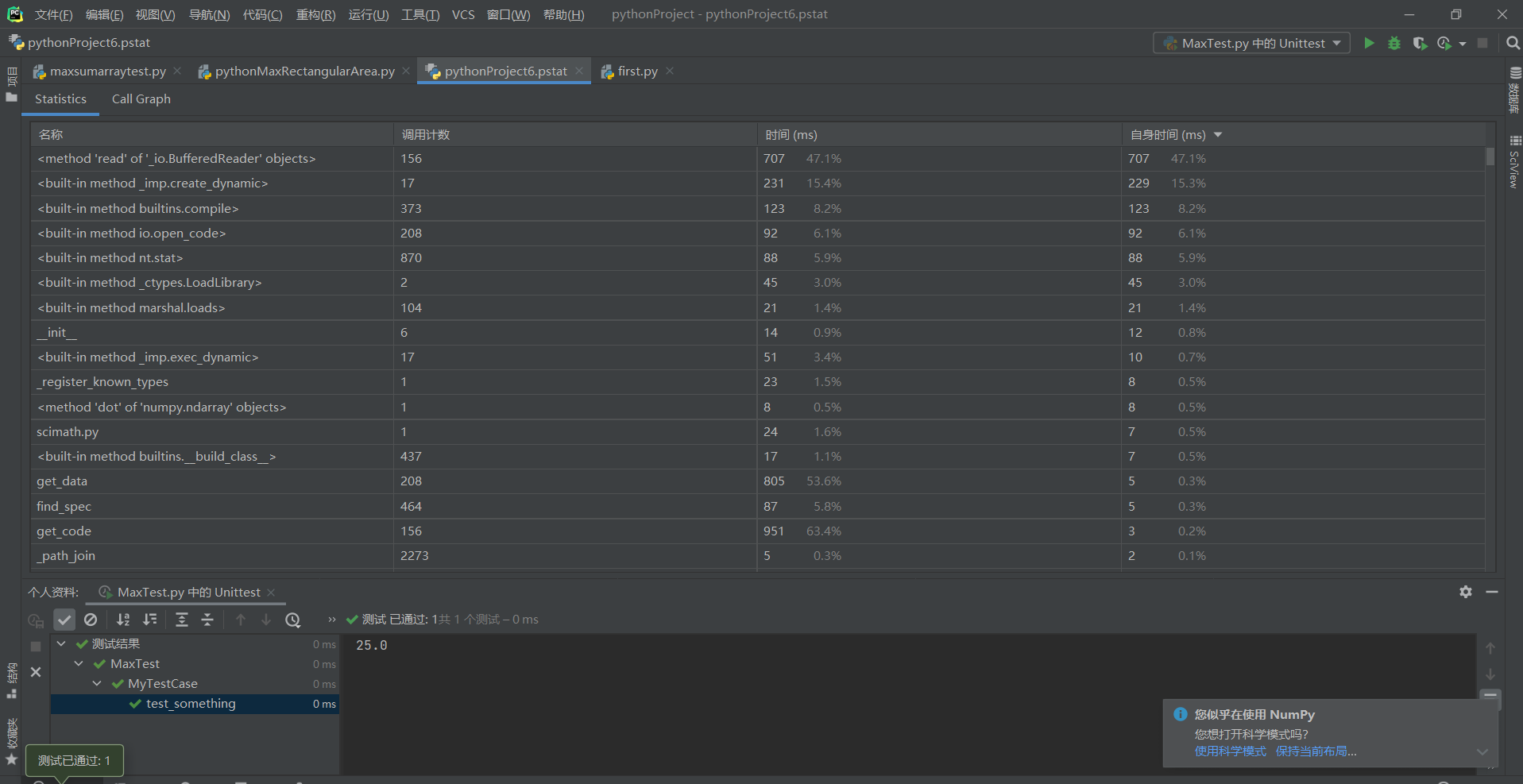
7、实验总结
1.代码覆盖率还行,函数中并无太多冗余。
2.通过简单的性能分析,了解到多重嵌套循环虽然想清楚后容易实现但是复杂度过高
3.通过这次实践,更熟练运用了pycharm中的各种分析工具




 浙公网安备 33010602011771号
浙公网安备 33010602011771号