题解：AT_abc131_e [ABC131E] Friendships

前言

这是本人第一篇题解。

题意

构造一个简单图（没有重边与自环）。图中总共有 \(N\) 个节点，分别为 \(1\) 到 \(N\)。总共有 \(M\) 条边，每一条边的长度均为 \(1\)。有且仅有 \(K\) 对节点 \((u,v)\) 满足 \(u\) 到 \(v\) 的最短距离为 \(2\)。若不存在这样的图，输出 −1，否则给出任何一种满足条件的图。

思路

这是一道简单的构造题，可以想到菊花图(或树)。

如图：

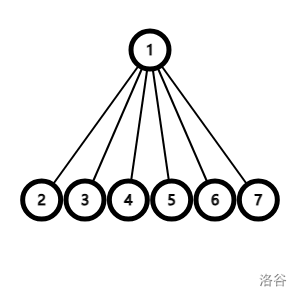
图中一共有 \(\frac{(N-1)\times(N-2)}{2}\) 对距离为 \(2\) 的点。

所以，还需要减去 \(\frac{(N-1)\times(N-2)}{2} - K\) 对距离为 \(2\) 的点。

如图，可以在 \(2\) 和 \(3\) 、 \(2\) 和 \(4\) 、 \(2\) 和 \(5\) 或 \(3\) 和 \(7\) 等连边即可，直到减完为止。

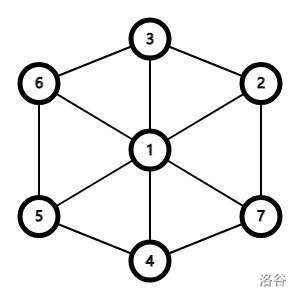
Code

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,m,b;
signed main(){
    scanf("%lld%lld",&n,&m);
    int q=(n-1)*(n-2)/2;
    if(m>q){
        printf("-1");
        return 0;
    }
    int o=q-m;
    b=o+n-1;
    printf("%lld\n",b);
    for(int i=2;i<=n;i++){
        cout<<"1 "<<i<<endl;
    }
    for(int i=2;i<=n;i++){
        for(int j=i+1;j<=n;j++){
            if(i==j)continue;
            if(!o)return 0;
            cout<<i<<" "<<j<<endl;
            o--;
        }
    }
    return 0;
}