第八节 求解Ax=b的可解性和结构

第八节 求解Ax=b的可解性和结构

可解性

仍取矩阵\(A\)为\({ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }2\text{ }\text{ }2\text{ }\text{ }2}\\ {2\text{ }\text{ }4\text{ }\text{ }6\text{ }\text{ }8}\\ {3\text{ }\text{ }6\text{ }\text{ }8\text{ }10} \end{array} \right] }}\right. }\)

这对应的\(Ax=b\)形式为：\({ \left[ {{\left. \begin{array}{*{20}{l}} {1\text{ }\text{ }2\text{ }\text{ }2\text{ }\text{ }2}\\ {2\text{ }\text{ }4\text{ }\text{ }6\text{ }\text{ }8}\\ {3\text{ }\text{ }6\text{ }\text{ }8\text{ }10} \end{array} \right] }}\right. }{ \left[ {{\left. \begin{array}{*{20}{l}} {x\mathop{{}}\nolimits_{{1}}}\\ {x\mathop{{}}\nolimits_{{2}}}\\ {x\mathop{{}}\nolimits_{{3}}}\\ {x\mathop{{}}\nolimits_{{4}}} \end{array} \right] }}\right. }={ \left[ {{\left. \begin{array}{*{20}{l}} {b\mathop{{}}\nolimits_{{1}}}\\ {b\mathop{{}}\nolimits_{{2}}}\\ {b\mathop{{}}\nolimits_{{3}}} \end{array} \right] }}\right. }\)

1. 矩阵\(A\)的第三行是前两行的和，所以上式中\(b\)也应该满足\({b\mathop{{}}\nolimits_{{3}}=b\mathop{{}}\nolimits_{{1}}+b\mathop{{}}\nolimits_{{2x\mathop{{}}\nolimits_{{1}}}}}\)，方程才有解，否则无解

2. 检验\(Ax=b\)是否可解的方法就是对增广矩阵进行消元：

   

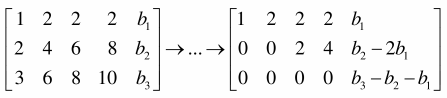
   如果\(Ax=b\)有解，则\({b\mathop{{}}\nolimits_{{3}}-b\mathop{{}}\nolimits_{{2}}-b\mathop{{}}\nolimits_{{1}}=0}\)，此时\({b={ \left[ {{\left. \begin{array}{*{20}{l}} {1}\\ {5}\\ {6} \end{array} \right] }}\right. }}\)

3. 前几节讨论过，只有\(b\)在矩阵\(A\)的列空间里时，才有解。这一节推导出，如果矩阵\(A\)的行向量经过线性组合成为了零向量，这对应的\(b\)也要经过同样的线性组合也要等于0，方程才有解。看似这是两个条件，但是它们是等价的

通解和特解

1. 通解

   • 假设\(Ax= 0\)的零空间的任意向量是\({x\mathop{{}}\nolimits_{{n}}}\)，\(Ax = b\)有一个特解\({x\mathop{{}}\nolimits_{{p}}}\)，那么有：

   \({\begin{array}{*{20}{l}} {{Ax\mathop{{}}\nolimits_{{p}}=b,}Ax\mathop{{}}\nolimits_{{n}}=0}\\ {{Ax\mathop{{}}\nolimits_{{p}}+Ax\mathop{{}}\nolimits_{{n}}=A \left( x\mathop{{}}\nolimits_{{p}}+x\mathop{{}}\nolimits_{{n}} \left) =b\right. \right. }} \end{array}}\)

   所以方程组的通解是\({x\mathop{{}}\nolimits_{{n}}}+{x\mathop{{}}\nolimits_{{p}}}\)，即通解就是特解和矩阵零空间的向量相加

2. 特解

   • 特解的求法是对矩阵中自由列进行赋值，求出主变量

秩

矩阵的秩等于矩阵的主元数。如果矩阵的秩为\(r\)，则必有\(r<=m\)且\(r<=n\)，下面讨论满秩（full rank）的情形：

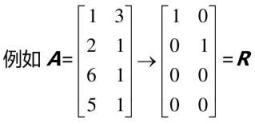
1. 列满秩：\(r=n\)

   • 每列都有主元，x的每一个分量都是主变量，没有自由变量

   • 零空间\(N(A)\)之内只有零向量

     为何列满秩时，零空间\(N(A)\)之内只有零向量？

     因为列满秩时，各列之间是线性无关的，也就是说无法通过线性变换结果为0；或者说没有自由变量可以赋值，只能让\(x=0\)，所以列满秩时，零空间\(N(A)\)之内只有零向量

   • 方程无解或者有唯一解

     为何列满秩时，方程无解或者有唯一解？

     刚才说过列满秩时，零空间\(N(A)\)之内只有零向量，所以方程的通解=特解，而特解取决于\(b\)，只有\(b\)正好是矩阵A列的线性组合时，方程才有唯一解，否则无解

   • 

2. 行满秩：\(r=m\)

   • 每行都有主元

   • 无论\(b\)取何值，方程\(Ax=b\)都有解

     为什么论\(b\)取何值，方程\(Ax=b\)都有解？

     因为行满秩时，矩阵\(A\)没有空行，也就是行之间是线性无关的，所以对\(b\)没有限制条件。也就是说不管\(b\)取什么值，只要调整自由变量就可以让等式成立

   • 主变量\(r\)个，自由变量\(n-r\)个

   • 

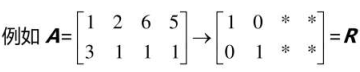
3. 满秩：\(r=m=n\)

   • 矩阵可逆
   • 零空间只有零向量
   • 无论\(b\)取何值，方程\(Ax=b\)都有唯一解
   • 

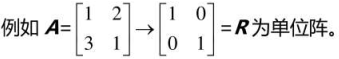
总结

秩决定了方程组解的数量