卡尔曼滤波是一种用于估计动态架构状态的最优递归数据处理算法，它依据结合系统模型的预测和传感器的测量信息，在最小化均方误差的意义下供应架构状态的最优估计。从数学角度看，卡尔曼滤波是一个线性递推估计器，它基于线性随机差分方程和线性测量方程，通过递归计算实现对系统状态的最优估计。​更正式地说，卡尔曼滤波处理的是一个离散时间线性随机系统，其状态方程和测量方程分别为：两个X_k一个是观测出

在动态系统的状态估计领域，卡尔曼滤波 (Kalman Filter) 作为一种最优线性滤波算法，具有里程碑式的地位。自 1960 年由鲁道夫・卡尔曼 (Rudolf E. Kalman) 提出以来，卡尔曼滤波已经广泛应用于导航、控制、信号处理、图像处理等众多领域。它的核心优势在于能够通过融合系统模型预测和传感器测量这两种不同来源的信息，提供最优的状态估计结果，专门适用于处理带有噪声的数据。​

卡尔曼滤波的卓越性能源于其独特的递归结构，它不需要存储所有历史数据，而是利用不断更新当前状态估计，高效地实现了实时处理。这种特性使得卡尔曼滤波在数字计算设备上的实现变得可行，特别是在当今实时性要求极高的自动驾驶、无人机导航等应用场景中发挥着不可替代的作用。​

卡尔曼滤波的定义与基本原理

卡尔曼滤波的定义

卡尔曼滤波是一种用于估计动态平台状态的最优递归数据处理算法，它通过结合架构模型的预测和传感器的测量信息，在最小化均方误差的意义下提供系统状态的最优估计。从数学角度看，卡尔曼滤波是一个线性递推估计器，它基于线性随机差分方程和线性测量方程，凭借递归计算实现对系统状态的最优估计。​

更正式地说，卡尔曼滤波处理的是一个离散时间线性随机系统，其状态方程和测量方程分别为：

两个X_k一个是观测出来的，另一个是预测的

卡尔曼滤波的基本假设

卡尔曼滤波基于以下几个关键假设：​

1. 线性系统假设：系统的状态转移和测量模型都是线性的。这意味着状态向量和测量向量之间存在线性关系，如上述的状态方程和测量方程所示。​
2. 高斯噪声假设：过程噪声和测量噪声均为高斯白噪声，且互不相关。这一假设使得卡尔曼滤波能够在最小均方误差意义下获得最优估计。​
3. 初始状态的统计特性已知：体系的初始状态x_0的均值和协方差矩阵是已知的，或者可能合理估计。​

当这些假设条件不满足时，标准卡尔曼滤波可能需要进行调整或扩展，如扩展卡尔曼滤波 (EKF) 用于非线性系统，无迹卡尔曼滤波 (UKF) 用于强非线性框架等。

卡尔曼滤波的核心思想

卡尔曼滤波的核心思想可以概括为 “预测 - 更新” 的循环过程：​

1. 预测步骤：基于系统的动态模型和上一时刻的最优估计，预测当前时刻的状态估计和协方差矩阵​。​
2. 更新步骤：利用当前时刻的测量数据，对上一步的预测结果进行修正，得到当前时刻的最优估计​。​

这种循环过程使得卡尔曼滤波能够不断地融合新的测量信息，逐步修正估计结果，从而实现对系统状态的动态跟踪。卡尔曼滤波的递归特性使其特别适合实时应用，因为它不需要存储所有历史数据，只需要维护当前的状态估计和协方差矩阵​。

卡尔曼滤波的算法流程

卡尔曼滤波的两大阶段

卡尔曼滤波算法可以分为两个关键阶段：预测阶段和更新阶段。这两个阶段不断交替执行，形成一个闭环反馈系统，使得状态估计能够不断优化。​

1. 预测阶段的主要功能是基于系统模型和上一时刻的最优估计，预测当前时刻的状态和协方差矩阵。预测阶段产生的结果称为先验估计 (priori estimate)，即基于先验知识 (系统模型) 得到的估计结果。​
2. 更新阶段利用当前时刻的测量数据，对预测阶段的结果进行修正，得到当前时刻的最优估计。更新阶段产生的结果称为后验估计 (posteriori estimate)，即融合了新测量信息后的估计结果。​就是的主要功能

这两个阶段的具体实现涉及五个基本方程，这些方程构成了卡尔曼滤波的核心算法。

卡尔曼滤波的五个基本方程

卡尔曼滤波算法由以下五个基本方程组成，这些方程分为预测和更新两个阶段：

状态预测方程

协方差预测方程

卡尔曼增益计算方程

状态更新方程

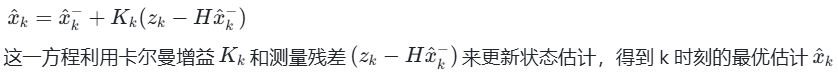
协方差更新方程

这五个方程构成了卡尔曼滤波的核心算法，它们按照上述顺序依次执行，形成一个完整的卡尔曼滤波周期。

卡尔曼滤波的完整算法流程

基于上述五个基本方程，卡尔曼滤波的完整算法流程行描述如下：​

1. 初始化：在第一个时间步 (k=0)，需要初始化状态估计x^0和协方差矩阵P_0。这些初始值通常基于对系统的先验知识或初始测量确定。​

2. 预测阶段：​

   • 使用状态预测方程计算先验状态估计x^k−
   • 启用协方差预测方程计算先验协方差矩阵P k−

3. 更新阶段：​

   • 当新的测量z_k到达时，计算卡尔曼增益K_k
   • 运用状态更新方程计算后验状态估计x^k
   • 使用协方差更新方程计算后验协方差矩阵P_k

4. ​循环：将 k 增加 1，返回预测阶段，重复上述过程​

卡尔曼滤波的这种递归结构使其特别适合实时应用，因为它不需要存储所有历史数据，只需要维护当前的状态估计和协方差矩阵。

卡尔曼滤波的算法流程图

为了更直观地理解卡尔曼滤波的算法流程，下面以流程图的形式展示其主要步骤​：

开始
|
v
初始化: x0, P0
|
v
循环: 对每个时间步k
|   |
|   v
|   预测阶段:
|   |   xk- = A * xk-1 + B * uk-1
|   |   Pk- = A * Pk-1 * A^T + Q
|   |
|   v
|   更新阶段:
|   |   Kk = Pk- * H^T * inv(H * Pk- * H^T + R)
|   |   xk = xk- + Kk * (zk - H * xk-)
|   |   Pk = (I - Kk * H) * Pk-
|   |
|   v
|   k = k + 1
|
v
结束

这一流程图清晰地展示了卡尔曼滤波的预测 - 更新循环过程，其中每个步骤都基于前一步的结果，形成一个闭环反馈系统。

卡尔曼增益的深入解析

卡尔曼增益的定义与数学表达式

卡尔曼增益 (Kalman Gain) 是卡尔曼滤波算法中的关键参数，它决定了测量更新对状态估计的影响程度。在数学上，卡尔曼增益K_k的表达式为：

卡尔曼增益的直观含义

从直观上看，卡尔曼增益K_k表示的是测量更新在状态估计中的权重。它实际上是一个最优加权因子，用于平衡系统模型预测和实际测量这两种不同来源的信息​

当卡尔曼增益K_k较大时，说明算法更信任测量资料，此时测量更新对状态估计的影响较大；反之，当卡尔曼增益
​K_k较小时，说明算法更信任系统模型预测，测量更新对状态估计的影响较小​

卡尔曼滤波的核心优势之一，它允许算法根据体系的动态特性和测量的可靠性自动调整对不同信息源的信任程度就是这种平衡机制

卡尔曼增益的作用分析

卡尔曼增益在卡尔曼滤波中发挥着多方面的关键作用，主要包括以下几点：​
最优信息融合​
卡尔曼增益的主要作用是搭建平台模型预测和传感器测量这两种信息的最优融合。通过最小化均方误差，卡尔曼增益确保了融合后的状态估计是最优的。​
在数学上，卡尔曼增益的推导过程实际上是一个优化问题，目标是找到最优的加权矩阵K_k，使得后验估计的均方误差最小。这一优化挑战的解正是上述的卡尔曼增益表达式。​
测量更新的比例控制​
卡尔曼增益控制着测量更新对状态估计的影响程度。具体来说，测量更新项为K_k(z_k−Hx_k⁻​ )，其中(z_k −Hx_k⁻)是测量残差，表示预测值与实际测量值之间的差异。​
卡尔曼增益​K_k将这一残差转换为状态估计的修正量，其大小决定了修正量的比例。通过调整卡尔曼增益，可以控制测量更新对状态估计的影响程度。​
噪声抑制与信号提取​
抑制噪声并提取有用信号。在有噪声的测量环境中，卡尔曼增益能够根据噪声特性自动调整滤波特性，有效抑制测量噪声的影响。​就是卡尔曼增益的另一个要紧作用
当测量噪声较大 (R 较大) 时，卡尔曼增益会自动减小，降低测量更新的影响，从而抑制噪声；当测量噪声较小时，卡尔曼增益会自动增大，更多地利用测量信息进行更新。​
动态调整滤波特性​
能够根据架构的动态特性和测量噪声特性自动调整滤波特性。这种自适应能力使得卡尔曼滤波能够在不同的工作条件下保持最优性能。​就是卡尔曼增益的一个显著优势
例如，在系统动态变化剧烈的情况下，过程噪声协方差矩阵 Q 会增大，导致卡尔曼增益自动增大，更多地依赖测量信息进行更新；而在系统动态变化平缓的情况下，卡尔曼增益会自动减小，更多地依赖系统模型预测。

卡尔曼增益的调整策略

在实际应用中，卡尔曼增益的调整是优化卡尔曼滤波性能的关键。以下是一些常见的卡尔曼增益调整策略：​
根据噪声特性调整：通过通过调整过程噪声协方差矩阵 Q 和测量噪声协方差矩阵 R，能够间接调整卡尔曼增益的大小。增加 Q 会使卡尔曼增益增大，更多地依赖测量；增加 R 会使卡尔曼增益减小，更多地依赖预测。​
自适应调整：在某些应用中，可以根据测量残差的统计特性在线调整 Q 和 R，从而实现卡尔曼增益的自适应调整。​
渐消记忆调整：在系统参数可能发生变化的情况下，可以采用渐消记忆技术，通过引入遗忘因子来调整卡尔曼增益，增强滤波对时变平台的跟踪能力。​
多模型调整：在复杂环境下，可以使用多个卡尔曼滤波器并行工作，每个滤波器使用不同的模型和参数，然后依据某种方式融合它们的输出。​
这些调整策略可以帮助优化卡尔曼滤波的性能，使其在各种实际应用中发挥最佳效果。