打卡信奥刷题(2061)用C++构建信奥 P11385 [POI 2024/2025 R1] Walki robotów
P11385 [POI 2024/2025 R1] Walki robotów
题目背景
原题译自 POI 2024/2025 R1 Walki robotów。
题目描述
在 Bajtocji 正在进行一场大型年度机器人锦标赛,其中有 n n n 个机器人参赛,它们的编号从 1 1 1 到 n n n。第 i i i 个机器人由两个参数描述, s i s_{i} si 和 z i ( 1 ≤ s i , z i ≤ n ) z_{i}\ (1 \leq s_{i}, z_{i} \leq n) zi(1≤si,zi≤n),分别表示机器人的力量和敏捷度。力量值 s i s_{i} si 各不相同。敏捷度值 z i z_{i} zi 也各不相同。
锦标赛由一系列单挑比赛组成。在每场比赛中,两个尚未被淘汰的机器人进行对决。在第 i i i 个机器人对战第 j j j 个机器人的比赛中,如果 s i > s j s_{i}>s_{j} si>sj 或 z i > z j z_{i}>z_{j} zi>zj,那么第 i i i 个机器人将淘汰第 j j j 个机器人。相应地,如果 s i < s j s_{i}<s_{j} si<sj 或 z i < z j z_{i}<z_{j} zi<zj,那么第 j j j 个机器人将淘汰第 i i i 个机器人。请注意,这意味着在同一场比赛中可能会有两个机器人都被淘汰。如果某个机器人没有在比赛中被淘汰,它可以继续参与后续比赛。
只有当最终所有机器人都被淘汰时,锦标赛的直播收视率才能最高。你的任务是检查是否可以安排一系列比赛,使得最终所有机器人都被淘汰。
输入格式
输入的第一行包含一个整数 n ( 1 ≤ n ≤ 2 ⋅ 1 0 5 ) n\ (1 \leq n \leq 2\cdot 10^5) n(1≤n≤2⋅105)。接下来的 n n n 行描述了机器人的信息。第 i i i 个机器人的描述包含两个整数 s i s_{i} si 和 z i ( 1 ≤ s i , z i ≤ n ) z_{i}\ (1 \leq s_{i}, z_{i} \leq n) zi(1≤si,zi≤n)。保证 s 1 , s 2 , … , s n s_{1}, s_{2}, \ldots, s_{n} s1,s2,…,sn 互不相同。保证 z 1 , z 2 , … , z n z_{1}, z_{2}, \ldots, z_{n} z1,z2,…,zn 互不相同。即 s , z s,z s,z 都是 1 ∼ n 1 \sim n 1∼n 的两个排列。
输出格式
如果可以安排一系列比赛,使得最终所有机器人都被淘汰,则输出 TAK。否则,输出 NIE。
输入输出样例 #1
输入 #1
4
1 4
2 2
3 3
4 1输出 #1
TAK输入输出样例 #2
输入 #2
2
1 1
2 2输出 #2
NIE输入输出样例 #3
输入 #3
见下发 wal1ocen.in输出 #3
见下发 wal1ocen.out输入输出样例 #4
输入 #4
见下发 wal2ocen.in输出 #4
见下发 wal2ocen.out输入输出样例 #5
输入 #5
见下发 wal3ocen.in输出 #5
见下发 wal3ocen.out输入输出样例 #6
输入 #6
见下发 wal4ocen.in输出 #6
见下发 wal4ocen.out输入输出样例 #7
输入 #7
见下发 wal5ocen.in输出 #7
见下发 wal5ocen.out说明/提示
对于样例一,如果在第一场比赛中第一个和第二个机器人对决,第二场比赛中第三个和第四个机器人对决,那么所有机器人都将被淘汰。
对于样例三,该样例满足 n = 8 , s i = i , z i = n − i + 1 n=8, s_{i}=i, z_{i}=n-i+1 n=8,si=i,zi=n−i+1。
对于样例四,该样例满足 n = 20 n=20 n=20,存在一个机器人可以击败所有其他机器人,并且没有机器人可以击败它。
对于样例五,该样例满足 n = 500 n=500 n=500,可以将所有机器人配对,使每对机器人互相淘汰。
对于样例六,该样例满足 n = 200000 , s i = i n=200000, s_{i}=i n=200000,si=i 且 z i = i z_{i}=i zi=i 对 1 ≤ i ≤ n 2 1 \leq i \leq \frac{n}{2} 1≤i≤2n,并且 s i = i s_{i}=i si=i 且 z i = 3 n 2 − i + 1 z_{i}=\frac{3n}{2}-i+1 zi=23n−i+1 对 n 2 < i ≤ n \frac{n}{2}<i \leq n 2n<i≤n。
对于样例七,该样例满足 n = 5 n=5 n=5。
| 子任务编号 | 特殊性质 | 分值 |
|---|---|---|
| 1 1 1 | n ≤ 8 n \leq 8 n≤8 | 10 10 10 |
| 2 2 2 | n ≤ 20 n \leq 20 n≤20 | 10 10 10 |
| 3 3 3 | n ≤ 1000 n \leq 1000 n≤1000 | 30 30 30 |
| 4 4 4 | 无特殊性质 | 50 50 50 |
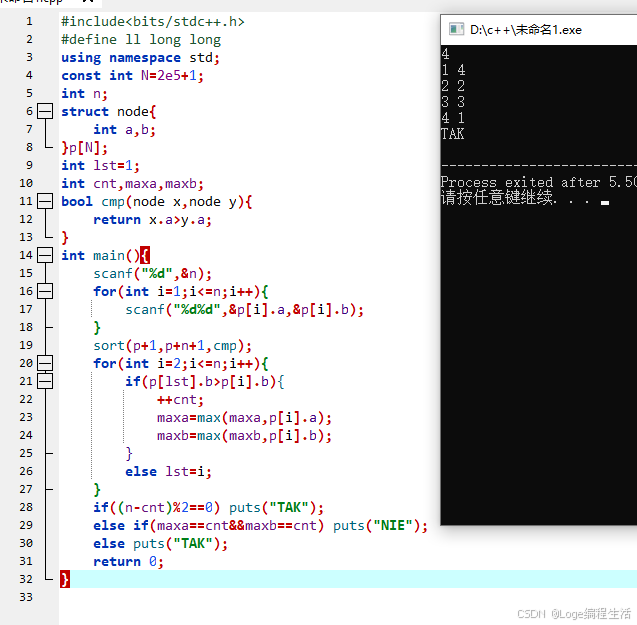
C++实现
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=2e5+1;
int n;
struct node{
int a,b;
}p[N];
int lst=1;
int cnt,maxa,maxb;
bool cmp(node x,node y){
return x.a>y.a;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d",&p[i].a,&p[i].b);
}
sort(p+1,p+n+1,cmp);
for(int i=2;i<=n;i++){
if(p[lst].b>p[i].b){
++cnt;
maxa=max(maxa,p[i].a);
maxb=max(maxb,p[i].b);
}
else lst=i;
}
if((n-cnt)%2==0) puts("TAK");
else if(maxa==cnt&&maxb==cnt) puts("NIE");
else puts("TAK");
return 0;
}
后续
接下来我会不断用C++来实现信奥比赛中的算法题、GESP考级编程题实现、白名单赛事考题实现,记录日常的编程生活、比赛心得,感兴趣的请关注,我后续将继续分享相关内容




 浙公网安备 33010602011771号
浙公网安备 33010602011771号