计算方法 - 指南

注：本文为 “线性代数 · 矩阵 | 秩” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未全校去重。
如有内容异常，请看原文。

矩阵的秩及其应用

一、矩阵秩的基本概念

（一）k 阶子式

设矩阵 $(a_{ij})_{m \times n}$ ，在矩阵 $A$ 中任意选取 $k$ 行（ $\leq k \leq m$ ）和 $k$ 列（ $\leq k \leq n$ ），将位于这些行与列交叉处的 $k^2$ 个元素按原有的相对位置组成一个 $k$ 阶行列式，该行列式称为矩阵 $A$ 的一个 k 阶子式。

对于 $\times n$ 矩阵 $A$ ， $k$ 阶子式的总数为组合数 $\mathrm{C}_{m}^{k} \times \mathrm{C}_{n}^{k}$ （其中 $\mathrm{C}_{n}^{k} = \frac{n!}{k!(n - k)!}$ 表示从 $n$ 个元素中选取 $k$ 个元素的组合数）。

示例：设矩阵 $\begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 4 & 1 \\ 1 & 4 & 1 & 2 \end{pmatrix}$

选取第 1、2 行和第 2、4 列，交叉处元素组成的 2 阶子式为 $D_2' = \begin{vmatrix} 2 & 4 \\ 3 & 1 \end{vmatrix}$ ；
选取第 1、3 行和第 1、3 列，交叉处元素组成的 2 阶子式为 $D_2'' = \begin{vmatrix} 1 & 3 \\ 1 & 1 \end{vmatrix}$ ；
该矩阵的 2 阶子式总数为 $\mathrm{C}_{3}^{2} \times \mathrm{C}_{4}^{2} = 3 \times 6 = 18$ ，3 阶子式总数为 $\mathrm{C}_{3}^{3} \times \mathrm{C}_{4}^{3} = 1 \times 4 = 4$ 。

（二）矩阵秩的定义

设矩阵 $(a_{ij})_{m \times n}$ ，若存在一个 $r$ 阶子式不为 $0$ ，且所有 $r + 1$ 阶子式（若存在）全为 $0$ ，则称 $r$ 为矩阵 $A$ 的秩，记作 $R (A)$ 或 $\mathrm{rank}(A)$ 。

特殊规定：零矩阵（所有元素均为 $0$ 的矩阵）的秩为 $0$ ，即 $R (0) = 0$ 。

重要结论：

对任意 $\times n$ 矩阵 $A$ ，必有 $\leq R(A) \leq \min\{m, n\}$ ；
若 $n$ 阶方阵 $A$ 的秩 $R (A) = n$ ，则称 $A$ 为 满秩矩阵（或非奇异矩阵），此时 $\det(A) \neq 0$ （ $\det(A)$ 表示矩阵 $A$ 的行列式）；
若 $n$ 阶方阵 $A$ 的秩 $R (A) < n$ ，则称 $A$ 为 降秩矩阵（或奇异矩阵），此时 $\det(A) = 0$ 。

（三）秩的等价描述

矩阵的秩本质反映了矩阵中行（或列）向量的线性无关性，具体等价描述如下：

行秩：矩阵 $A$ 的行向量组中线性无关的行向量的最大个数；
列秩：矩阵 $A$ 的列向量组中线性无关的列向量的最大个数；
定理：对任意矩阵 $A$ ，其行秩 = 列秩 = 秩（即 $\text{行秩} = \text{列秩}$ ）。

二、矩阵秩的计算方法

（一）子式判别法（定义法）

根据矩阵秩的定义，通过寻找“最高阶非零子式”来确定秩，步骤如下：

否全为就是从低阶子式开始计算，先判断 1 阶子式（即矩阵元素） $0$ ：若全为 $0$ ，则 $R (A) = 0$ ；若存在非零 1 阶子式，继续判断 2 阶子式；
若存在非零 2 阶子式，继续判断 3 阶子式，以此类推；
找到最大的 $r$ ，使得存在非零 $r$ 阶子式，且所有 $r + 1$ 阶子式全为 $0$ ，则 $R (A) = r$ 。

示例 1：求矩阵 $\begin{pmatrix} 1 & 2 & 3 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}$ 的秩

选取第 1、2、3 行和第 1、2、3 列，组成的 3 阶子式为 $\begin{vmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = 1 \neq 0$ ；
矩阵 $A$ 为 $\times 4$ 矩阵，不存在 4 阶子式；
因此 $R (A) = 3$ 。

示例 2：求矩阵 $\begin{pmatrix} 1 & 2 & 5 \\ 0 & 3 & 4 \\ 0 & 0 & 0 \end{pmatrix}$ 的秩

1 阶子式（如元素 $1$ 、 $2$ 、 $5$ 等）非零，2 阶子式（如 $\begin{vmatrix} 1 & 2 \\ 0 & 3 \end{vmatrix} = 3 \neq 0$ ）非零；
所有 3 阶子式（仅 1 个，即矩阵 $D$ 的行列式）为 $\begin{vmatrix} 1 & 2 & 5 \\ 0 & 3 & 4 \\ 0 & 0 & 0 \end{vmatrix} = 0$ ；
因此 $R (D) = 2$ （原内容此处写为 $R (A)$ ，属于符号混淆，已修正为 $R (D)$ ）。

（二）初等变换法（最常用方法）

1. 重要定理

矩阵的初等变换（行变换或列变换）不改变矩阵的秩，即若矩阵 $A$ 经过初等变换化为矩阵 $B$ ，则 $R (A) = R (B)$ 。

初等变换的类型：

行变换：
1. 交换两行（记为 $r_i \leftrightarrow r_j$ ）；
2. 用非零常数 $k$ 乘某一行（记为 $k r_i$ ， $\neq 0$ ）；
3. 某一行的 $k$ 倍加到另一行（记为 $r_i + k r_j$ ）。
列变换：
1. 交换两列（记为 $c_i \leftrightarrow c_j$ ）；
2. 用非零常数 $k$ 乘某一列（记为 $k c_i$ ， $\neq 0$ ）；
3. 某一列的 $k$ 倍加到另一列（记为 $c_i + k c_j$ ）。

2. 行阶梯形矩阵的定义

满足以下两个条件的矩阵称为行阶梯形矩阵：

全零行（所有元素均为 $0$ 的行）位于矩阵的下方；
非零行的第一个非零元素（称为“主元”）的列序数，从上到下严格递增。

示例： $\begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ 是行阶梯形矩阵（主元分别在第 1 列、第 2 列，列序数递增，全零行在最下方）。

3. 计算步骤

对矩阵 $A$ 施行初等行变换，将其化为行阶梯形矩阵 $B$ ；
行阶梯形矩阵 $B$ 中非零行的行数，即为矩阵 $A$ 的秩（ $\text{非零行数}$ ）。

示例 1：求矩阵 $\begin{pmatrix} 1 & 0 & 2 & -4 \\ 2 & 1 & 3 & -6 \\ -1 & -1 & -1 & 2 \end{pmatrix}$ 的秩

第一步：消去第 1 列下方元素（以第 1 行第 1 列元素 $1$ 为主元）
$\xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ -1 & -1 & -1 & 2 \end{pmatrix} \xrightarrow{r_3 + r_1} \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \end{pmatrix}$ ；
第二步：消去第 2 列下方元素（以第 2 行第 2 列元素 $1$ 为主元）
$\xrightarrow{r_3 + r_2} \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ ；
行阶梯形矩阵中非零行的行数为 $2$ ，因此 $R (A) = 2$ 。

示例 2：求矩阵 $\begin{pmatrix} 4 & -2 & 1 \\ 1 & 2 & -2 \\ -1 & 8 & -7 \\ 2 & 14 & -13 \end{pmatrix}$ 的秩

第一步：交换第 1、2 行（使第 1 列主元为 $1$ ，简化计算）
$\xrightarrow{r_1 \leftrightarrow r_2} \begin{pmatrix} 1 & 2 & -2 \\ 4 & -2 & 1 \\ -1 & 8 & -7 \\ 2 & 14 & -13 \end{pmatrix}$ ；
第二步：消去第 1 列下方元素
$\xrightarrow{r_2 - 4 r_1} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ -1 & 8 & -7 \\ 2 & 14 & -13 \end{pmatrix} \xrightarrow{r_3 + r_1} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 10 & -9 \\ 2 & 14 & -13 \end{pmatrix} \xrightarrow{r_4 - 2 r_1} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 10 & -9 \\ 0 & 10 & -9 \end{pmatrix}$ ；
第三步：消去第 2 列下方元素
$\xrightarrow{r_3 + r_2} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 0 & 0 \\ 0 & 10 & -9 \end{pmatrix} \xrightarrow{r_4 + r_2} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}$ ；
行阶梯形矩阵中非零行的行数为 $2$ ，因此 $R (A) = 2$ 。

（三）含参数矩阵的秩（需分类讨论）

当矩阵中含参数时，需根据参数的取值判断最高阶非零子式的阶数，进而确定秩。

示例：设矩阵 $\begin{pmatrix} 1 & -1 & 1 & 2 \\ 3 & \lambda & -1 & 2 \\ 5 & 3 & \mu & 6 \end{pmatrix}$ ，且 $R (A) = 2$ ，求 $\lambda$ 和 $\mu$ 的值

第一步：对 $A$ 施行初等行变换化为行阶梯形
$\xrightarrow{r_2 - 3 r_1} \begin{pmatrix} 1 & -1 & 1 & 2 \\ 0 & \lambda + 3 & -4 & -4 \\ 5 & 3 & \mu & 6 \end{pmatrix} \xrightarrow{r_3 - 5 r_1} \begin{pmatrix} 1 & -1 & 1 & 2 \\ 0 & \lambda + 3 & -4 & -4 \\ 0 & 8 & \mu - 5 & -4 \end{pmatrix}$ ；
第二步：由 $R (A) = 2$ 可知，行阶梯形矩阵中第 3 行需为全零行，因此第 2、3 行对应元素成比例
即 $\frac{\lambda + 3}{8} = \frac{-4}{\mu - 5} = \frac{-4}{-4}$ ；
第三步：求解比例方程
由 $\frac{-4}{-4} = 1$ ，得 $\lambda + 3 = 8 \times 1 \implies \lambda = 5$ ； $(\mu - 5) \times 1 \implies \mu = 1$ ；
因此，当 $\lambda = 5$ 且 $\mu = 1$ 时， $R (A) = 2$ 。

三、矩阵化简的形式与方式

（一）矩阵化简的基本原理

矩阵化简依据初等变换（行变换或列变换）搭建，初等变换不改变矩阵的秩，是计算秩、求解线性方程组的关键工具。常见化简目标包括行阶梯形、行简化行阶梯形、列阶梯形及等价标准形，不同形式适用于不同场景。

（二）常见化简形式及规则

1. 行阶梯形（Row Echelon Form, REF）

REF 是“阶梯状”的基础化简形式，需满足以下 4 条规则：

全零行位于矩阵最下方；
非零行的第一个非零元素（称为“主元”）的列索引，严格大于上一行主元的列索引（形成“阶梯”结构）；
主元下方的所有元素全为 $0$ ；
主元可为任意非零数（无需强制为 $1$ ）。

示例（主元用橙色标注）：
$\begin{pmatrix} \color{orange}{2} & 3 & 5 & 7 \\ 0 & \color{orange}{-1} & 4 & 2 \\ 0 & 0 & 0 & \color{orange}{3} \\ 0 & 0 & 0 & 0 \end{pmatrix}$

用途：飞快判断矩阵的秩（非零行数 = 秩）；初步求解线性方程组（需后续“回代”步骤）。
注意：一个矩阵的 REF 不唯一（主元可缩放，不同初等行变换可能得到不同 REF）。

2. 行简化行阶梯形（Reduced Row Echelon Form, RREF）

RREF 是 REF 的“最简形式”，在 REF 规则基础上额外满足 2 条严格规则：

所有主元的值必为 $1$ ；
主元上方的所有元素全为 $0$ （即主元列仅主元为 $1$ ，其余元素均为 $0$ ）。

示例（将上述 REF 化为 RREF，主元用橙色标注）：
$\begin{pmatrix} \color{orange}{1} & 0 & 17/2 & 0 \\ 0 & \color{orange}{1} & -4 & 0 \\ 0 & 0 & 0 & \color{orange}{1} \\ 0 & 0 & 0 & 0 \end{pmatrix}$

重要性质：一个矩阵的 RREF 是唯一的（无论采用何种初等行变换，最终结果完全相同）。
用途：直接读取线性方程组的解（无需回代）；确定矩阵的主元列（对应列空间的基）；判断向量组的线性相关性。

3. 列阶梯形（Column Echelon Form, CEF）

CEF 与 REF 逻辑对称，借助初等列变换实现，需满足以下 4 条规则：

全零列位于矩阵最右侧；
非零列的第一个非零元素（称为“列主元”）的行索引，严格大于左一列列主元的行索引；
列主元右侧的所有元素全为 $0$ ；
列主元可为任意非零数（无需强制为 $1$ ）。

示例（列主元用橙色标注）：
$\begin{pmatrix} \color{orange}{2} & 0 & 0 & 0 \\ 3 & \color{orange}{-1} & 0 & 0 \\ 5 & 4 & 0 & 0 \\ 7 & 2 & \color{orange}{3} & 0 \end{pmatrix}$

用途：分析矩阵的行空间（非零行是行空间的基）；计算矩阵的左逆（当矩阵列满秩时）。

4. 等价标准形（相抵标准形）

若同时允许初等行变换和初等列变换，任意 $\times n$ 矩阵可化为唯一的“等价标准形”，形式为：
$\mathbf{E} = \begin{pmatrix} \mathbf{I}_r & \mathbf{0}_{r \times (n-r)} \\ \mathbf{0}_{(m-r) \times r} & \mathbf{0}_{(m-r) \times (n-r)} \end{pmatrix}$
其中：

$m, n$ 分别为原矩阵的行数和列数；
$r = R (A)$ （矩阵的秩）；
$\mathbf{I}_r$ 为 $r$ 阶单位矩阵， $\mathbf{0}$ 为对应维度的零矩阵。

示例（秩为 $2$ 的 $\times 4$ 矩阵的等价标准形）：
$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$

用途：判断两个矩阵是否“等价”（若两个矩阵的等价标准形相同，则二者等价）；简化矩阵的秩与行列式计算。

（三）矩阵化简的应用场景总结

为清晰区分不同化简形式的适用场景，下表梳理了核心信息：

化简目标	推荐化简形式	操作方式	典型用途
快速计算矩阵的秩	行阶梯形（REF）	初等行变换	初步分析矩阵的有效维度，判断向量组线性相关性
求解线性方程组	行简化行阶梯形（RREF）	初等行变换	直接读取唯一解或无穷解的通解，无需回代
确定列空间的基	行简化行阶梯形（RREF）	初等行变换	主元列对应原矩阵的列向量，构成列空间的基
确定行空间的基	列阶梯形（CEF）	初等列变换	主元行对应原矩阵的行向量，构成行空间的基
判断两个矩阵是否等价	等价标准形	初等行变换 + 初等列变换	比较两个矩阵的结构相似度，验证是否可通过初等变换互化

四、矩阵秩的性质

设 $A$ 、 $B$ 为任意矩阵， $k$ 为非零常数， $n$ 为方阵的阶数，则矩阵的秩满足以下性质，下表结合“性质内容”与“直观说明”展开：

性质序号	性质内容	说明
1	$R(A^T) = R(A)$ （转置后秩不变）	矩阵的行秩 = 列秩，转置后行与列互换，秩的本质（线性无关向量的最大个数）不变
2	$\leq \min\{m, n\}$ （ $A$ 为 $\times n$ 矩阵）	秩反映矩阵的“有效维度”，无法超过矩阵的行数（行向量最大可能无关个数）或列数（列向量最大可能无关个数）
3	$R (k A) = R (A)$ （ $\neq 0$ ）	非零常数 $k$ 仅缩放矩阵元素，不改变子式的“非零性”（非零子式缩放后仍非零，零子式缩放后仍为零）
4	$\iff A = 0$ （零矩阵的充要条件）	零矩阵所有子式均为 $0$ ，故秩为 $0$ ；若 $R (A) = 0$ ，则无任何非零子式，矩阵必为零矩阵
5	$\leq R(A) + R(B)$ （和的秩不超过秩的和）	矩阵 $A + B$ 的行向量可由 $A$ 和 $B$ 的行向量组线性表示，因此其线性无关向量的最大个数不超过两组向量无关个数之和
6	$\leq \min\{R(A), R(B)\}$ （乘积的秩不超过因子矩阵的秩）	$A B$ 的列向量可由 $A$ 的列向量线性表示（故 $\leq R(A)$ ），行向量可由 $B$ 的行向量线性表示（故 $\leq R(B)$ ），因此取最小值
7	$\leq R(AB)$ （Sylvester 不等式）	对 $n$ 阶方阵 $A$ 、 $B$ ，乘积的秩存在下界，反映了因子矩阵秩与乘积矩阵秩的“关联约束”，可用于证明矩阵可逆性等问题
8	若 $A$ 为 $n$ 阶可逆矩阵，则 $R (A B) = R (B)$ ， $R (B A) = R (B)$	可逆矩阵可通过初等变换化为单位阵，而初等变换不改变矩阵的秩，因此 $A$ 的可逆性不影响 $B$ 的秩传递

五、矩阵秩的应用

矩阵的秩是连接“矩阵结构”与“线性代数疑问”的桥梁，以下从四个典型场景展开，结合示例说明其应用逻辑：

（一）判断线性方程组的解

对于线性方程组 $\boldsymbol{x} = \boldsymbol{b}$ （ $A$ 为 $\times n$ 系数矩阵， $\overline{A} = (A \mid \boldsymbol{b})$ 为增广矩阵），解的存在性与唯一性完全由 $R (A)$ 和 $R(\overline{A})$ 的关系决定，重点结论如下：

无解： $R(\overline{A})$ （增广矩阵的秩比系数矩阵多 $1$ ，对应矛盾方程 $\neq 0$ ，即“约束条件冲突”）；
唯一解： $R(\overline{A}) = n$ （秩等于未知数个数，无自由变量，即“约束条件恰好确定唯一解”）；
无穷多解： $R(\overline{A}) < n$ （秩小于未知数个数，存在自由变量，即“约束条件不足，解有多个”）。

示例：判断方程组 $\begin{cases} x_1 + 4 x_2 + 7 x_3 = 1 \\ 2 x_1 + 5 x_2 + 8 x_3 = 2 \\ 3 x_1 + 6 x_2 + 9 x_3 = 3 \end{cases}$ 的解

第一步：构造增广矩阵 $\overline{A} = \begin{pmatrix} 1 & 4 & 7 & 1 \\ 2 & 5 & 8 & 2 \\ 3 & 6 & 9 & 3 \end{pmatrix}$ ；
第二步：初等行变换化为行阶梯形：
$\overline{A} \xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 4 & 7 & 1 \\ 0 & -3 & -6 & 0 \\ 3 & 6 & 9 & 3 \end{pmatrix} \xrightarrow{r_3 - 3 r_1} \begin{pmatrix} 1 & 4 & 7 & 1 \\ 0 & -3 & -6 & 0 \\ 0 & -6 & -12 & 0 \end{pmatrix} \xrightarrow{r_3 - 2 r_2} \begin{pmatrix} 1 & 4 & 7 & 1 \\ 0 & -3 & -6 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ ；
第三步：分析秩的关系： $R (A) = 2$ ， $R(\overline{A}) = 2$ ，且未知数个数 $n = 3$ ，满足 $R(\overline{A}) < n$ ，因此方程组有无穷多解。

（二）判断向量组的线性相关性

设向量组 $\alpha_1, \alpha_2, \dots, \alpha_s$ 构成矩阵 $A$ （列向量组构成 $(\alpha_1, \alpha_2, \dots, \alpha_s)$ ，行向量组构成 $\begin{pmatrix} \alpha_1^T \\ \alpha_2^T \\ \dots \\ \alpha_s^T \end{pmatrix}$ ），则向量组的线性相关性与 $R (A)$ 的关系为：

若 $R (A) = s$ ，则向量组 线性无关（矩阵的秩等于向量个数，所有向量均可作为“有效约束”，无冗余）；
若 $R (A) < s$ ，则向量组 线性相关（矩阵的秩小于向量个数，存在冗余向量，可由其他向量线性表示）。

示例：判断向量组 $\alpha_1 = (1, 2, 3)^T$ ， $\alpha_2 = (2, 5, 8)^T$ ， $\alpha_3 = (3, 6, 9)^T$ 的线性相关性

构造矩阵 $(\alpha_1, \alpha_2, \alpha_3) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 5 & 6 \\ 3 & 8 & 9 \end{pmatrix}$ ；
初等行变换化为行阶梯形： $\xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 3 & 8 & 9 \end{pmatrix} \xrightarrow{r_3 - 3 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 2 & 0 \end{pmatrix} \xrightarrow{r_3 - 2 r_2} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix}$ ；
得 $R (A) = 2 < 3$ （向量个数），因此向量组线性相关。

（三）判断矩阵的可逆性

对 $n$ 阶方阵 $A$ ，“可逆性”与“秩”紧密关联，以下条件完全等价（可互相推导）：

$A$ 可逆（存在逆矩阵 $A^{-1}$ ，满足 $A^{-1} = A^{-1} A = \mathbf{I}_n$ ）；
$A$ 为满秩矩阵（ $R (A) = n$ ，即矩阵无冗余行/列，有用维度等于阶数）；
$\det(A) \neq 0$ （行列式非零，对应“最高阶子式非零”，符合满秩定义）；
$A$ 可凭借初等行变换化为单位阵 $\mathbf{I}_n$ （初等变换不改变秩，单位阵秩为 $n$ ，故 $A$ 秩也为 $n$ ）。

示例：设 $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 2 \\ 3 & 1 & 2 \end{pmatrix}$ ，验证 $A$ 可逆并化为单位阵

第一步：计算 $R (A)$ ：
$\xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 3 & 1 & 2 \end{pmatrix} \xrightarrow{r_3 - 3 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & -5 & -7 \end{pmatrix} \xrightarrow{r_3 - \frac{5}{3} r_2} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & 0 & -\frac{1}{3} \end{pmatrix}$ ；
行阶梯形中非零行数为 $3 = n$ （阶数），故 $R (A) = 3$ ， $A$ 可逆；
第二步：继续化为单位阵：
$\xrightarrow{r_3 \times (-3)} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_2 + 4 r_3} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_2 \times (-\frac{1}{3})} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_1 - 3 r_3} \begin{pmatrix} 1 & 2 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_1 - 2 r_2} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \mathbf{I}_3$ 。

（四）数据降维和信息压缩

在机器学习、信号处理等领域，矩阵的秩反映“数据冗余度”：低秩矩阵（ $\ll \min\{m, n\}$ ）表示信息存在大量冗余，可通过“保留核心信息、剔除冗余”完成降维与压缩，典型应用为奇异值分解（SVD） 和主成分分析（PCA）。

逻辑：对矩阵 $A$ 进行奇异值分解，得 $\Sigma V^T$ ，其中 $\Sigma$ 为对角矩阵，对角元素（奇异值）按从大到小排列；取前 $r$ 个非零奇异值（ $r = R (A)$ ）对应的子矩阵，可得到原矩阵的低秩逼近 $A_r = U_r \Sigma_r V_r^T$ ，实现用 $r (m + n - r)$ 个元素表示原 $\times n$ 矩阵（大幅减少存储量）。
示例：图片压缩。灰度图片可表示为 $\times n$ 矩阵（元素为像素灰度值），若矩阵秩 $r$ 远小于 $m$ 和 $n$ ，用低秩逼近矩阵 $A_r$ 替代原矩阵，视觉上几乎无差异，但存储量显著降低。

六、特殊矩阵的秩

部分结构特殊的矩阵，其秩可直接通过“直观特征”计算，无需复杂变换，以下列举两类典型矩阵：

（一）三角矩阵

三角矩阵分为上三角矩阵和下三角矩阵，其秩由“主对角线元素”直接决定：

上三角矩阵（主对角线下方元素全为 $0$ ）： $\begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ 0 & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & a_{nn} \end{pmatrix}$ ；
下三角矩阵（主对角线上方元素全为 $0$ ）： $\begin{pmatrix} a_{11} & 0 & \dots & 0 \\ a_{21} & a_{22} & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{pmatrix}$ ；
秩的计算规则：三角矩阵的秩等于主对角线上非零元素的个数。
（原因：三角矩阵的行列式为“主对角线元素乘积”，最高阶非零子式的阶数由非零对角元素的个数决定）。

示例：上三角矩阵 $\begin{pmatrix} 2 & 3 & 5 \\ 0 & 0 & 4 \\ 0 & 0 & -1 \end{pmatrix}$ ，主对角线元素为 $2, 0, - 1$ ，非零个数为 $2$ ，故 $R (A) = 2$ 。

（二）对角矩阵

特殊的三角矩阵（主对角线外元素全为就是对角矩阵 $0$ ），形式为： $\begin{pmatrix} a_{11} & 0 & \dots & 0 \\ 0 & a_{22} & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & a_{nn} \end{pmatrix}$ ；

秩的计算规则：对角矩阵的秩等于对角线上非零元素的个数（与三角矩阵规则一致，因对角矩阵同时属于上三角矩阵和下三角矩阵）。

示例：对角矩阵 $\begin{pmatrix} -3 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 5 \end{pmatrix}$ ，对角线上非零元素为 $- 3$ 和 $5$ ，共 $2$ 个，故 $R (B) = 2$ 。

七、MATLAB 计算矩阵秩的代码实现

在 MATLAB 中，可直接使用内置函数 rank() 快速计算矩阵的秩，其底层通过奇异值分解（SVD）实现，能有效避免数值误差对结果的影响。以下为具体实现步骤与示例：

% 1. 定义矩阵 A（以 3×3 矩阵为例）
A = [1 2 3;
4 5 6;
7 8 9];
% 2. 计算矩阵 A 的秩
rank_A = rank(A);
% 3. 显示结果
disp(['矩阵 A 的秩为: ', num2str(rank_A)]);

运行结果：矩阵 A 的秩为: 2（与通过初等变换手动计算的结果一致）。

说明：

rank() 函数的逻辑是：对矩阵进行奇异值分解，得到奇异值后，将小于某个阈值（默认约为 $10^{-15}$ ）的奇异值视为 $0$ ，非零奇异值的个数即为矩阵的秩；
阈值可通过函数参数调整，例如 rank(A, tol) 中 tol 为自定义阈值，适用于对数值精度有特殊要求的场景；
该函数适用于任意维度的矩阵（包括非方阵），是工程计算中高效可靠的秩计算应用。

八、例题解析：矩阵秩的应用

（一）题目

已知行简化行阶梯形矩阵 $\begin{pmatrix} 1 & 2 & 0 & 4 \\ 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 0 \end{pmatrix}$ ，完成以下任务：

求 $A$ 的秩；
求 $A$ 的行秩并验证其与秩的关系；
求 $A$ 的列秩并验证其与秩的关系。

（二）解答过程

1. 求矩阵 $A$ 的秩

根据“行阶梯形矩阵的秩等于非零行的行数”这一结论：

矩阵 $A$ 中，非零行包括第 1 行 $\begin{pmatrix} 1 & 2 & 0 & 4 \end{pmatrix}$ 和第 2 行 $\begin{pmatrix} 0 & 0 & 1 & 3 \end{pmatrix}$ ，共 $2$ 行；
零行仅第 3 行 $\begin{pmatrix} 0 & 0 & 0 & 0 \end{pmatrix}$ ，且位于所有非零行下方（符合行阶梯形结构）。

因此， $R (A) = 2$ 。

2. 求矩阵 $A$ 的行秩

矩阵 $A$ 的行向量组为：
$\alpha_1 = (1, 2, 0, 4),\ \alpha_2 = (0, 0, 1, 3),\ \alpha_3 = (0, 0, 0, 0)$

行秩是“行向量组中线性无关的最大向量个数”，分析如下：

线性无关性验证：假设存在常数 $k_1, k_2$ 使得 $k_1\alpha_1 + k_2\alpha_2 = \boldsymbol{0}$ （零向量），展开得：
$k_1, 2k_1, k_2, 4k_1 + 3k_2) = (0, 0, 0, 0)$
解得 $k_1 = 0$ 且 $k_2 = 0$ ，故 $\alpha_1, \alpha_2$ 线性无关；
最大性验证：零向量 $\alpha_3$ 可由 $\alpha_1, \alpha_2$ 线性表示（ $\alpha_3 = 0 \cdot \alpha_1 + 0 \cdot \alpha_2$ ），因此行向量组中线性无关的最大向量个数为 $2$ 。

因此， $A$ 的行秩为 $2$ ，且 $\text{行秩}$ 。

3. 求矩阵 $A$ 的列秩

矩阵 $A$ 的列向量组为：
$\beta_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\ \beta_2 = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix},\ \beta_3 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\ \beta_4 = \begin{pmatrix} 4 \\ 3 \\ 0 \end{pmatrix}$

列秩是“列向量组中线性无关的最大向量个数”，分析如下（选取主元列 $\beta_1, \beta_3$ 验证）：

线性无关性验证：假设存在常数 $l_1, l_3$ 使得 $l_1\beta_1 + l_3\beta_3 = \boldsymbol{0}$ （零向量），展开得：
$\begin{pmatrix} l_1 \\ l_3 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}$
解得 $l_1 = 0$ 且 $l_3 = 0$ ，故 $\beta_1, \beta_3$ 线性无关；
最大性验证：非主元列可由主元列线性表示：
- $\beta_2 = 2\beta_1 + 0 \cdot \beta_3$ ， $\beta_4 = 4\beta_1 + 3\beta_3$ ，因此列向量组中线性无关的最大向量个数为 $2$ 。

因此， $A$ 的列秩为 $2$ ，且 $\text{列秩} = \text{行秩}$ 。

（三）结论

理解矩阵结构与向量组关系的关键。就是通过例题验证，矩阵的秩、行秩与列秩三者完全相等，这一性质是矩阵理论的重要结论，也

九、总结

线性代数中刻画矩阵“本质维度”的重要概念，其定义基于子式的非零性，计算可通过子式判别法或更高效的初等变换法实现。矩阵的秩具有诸多关键性质，如转置不变性、乘积秩的有界性等，这些性质为分析矩阵关系提供了有力工具。就是矩阵的秩

在应用层面，矩阵的秩决定了线性方程组解的存在性与唯一性，可判断向量组的线性相关性，验证矩阵的可逆性，同时在数据降维、信息压缩等领域有广泛应用。掌握矩阵秩的概念、计算方法与应用场景，是学好线性代数的重要基础。

从两个角度看矩阵和向量相乘

Limi @_zhihu

前提条件

设矩阵 $A$ 与向量 $x$ 进行乘法运算，结果为向量 $b$ ，其维度与 $x$ 相同。进行此乘法运算的前提条件是矩阵 $A$ 的列数等于向量 $x$ 的行数。以下从两个方面探讨如何求得 $b$ ：行视角（Row Aspect）和列视角（Column Aspect）。

行视角（Row Aspect）

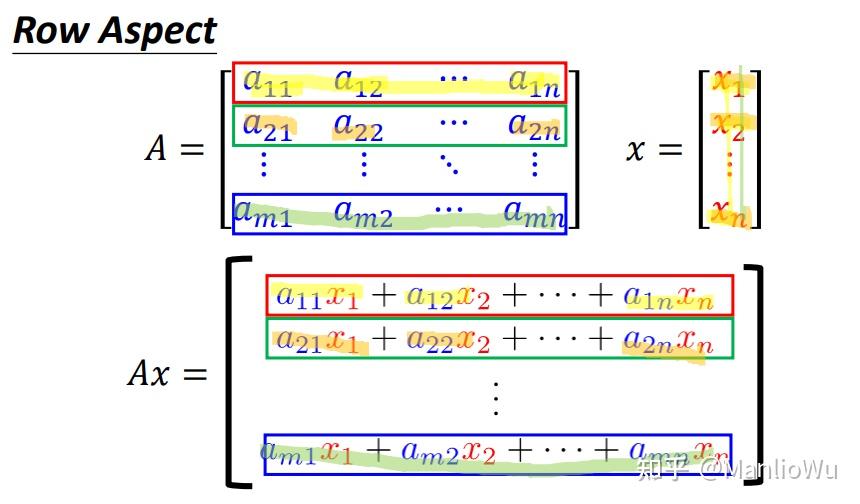
将矩阵 $A$ 视作“行向量的堆叠”，即 $A$ 的每一行均为一个向量。则向量 $b$ 的第 $i$ 个维度的值为 $A$ 的第 $i$ 行向量与 $x$ 作内积的结果，即 $b_i = (A_i, x)$ 。内积运算要求两个向量的维度相同，这也解释了矩阵与向量相乘时矩阵列数与向量行数需相等的原因。此外，在矩阵 $\times$ 矩阵的运算中，常采用的计算方法为：矩阵 $A$ 的第 $i$ 行与矩阵 $B$ 的第 $j$ 列相乘，结果为 $C_{i,j}$ 。矩阵 $\times$ 向量可视为矩阵 $\times$ 矩阵的特殊情形，即右侧矩阵仅有一列。

列视角（Column Aspect）

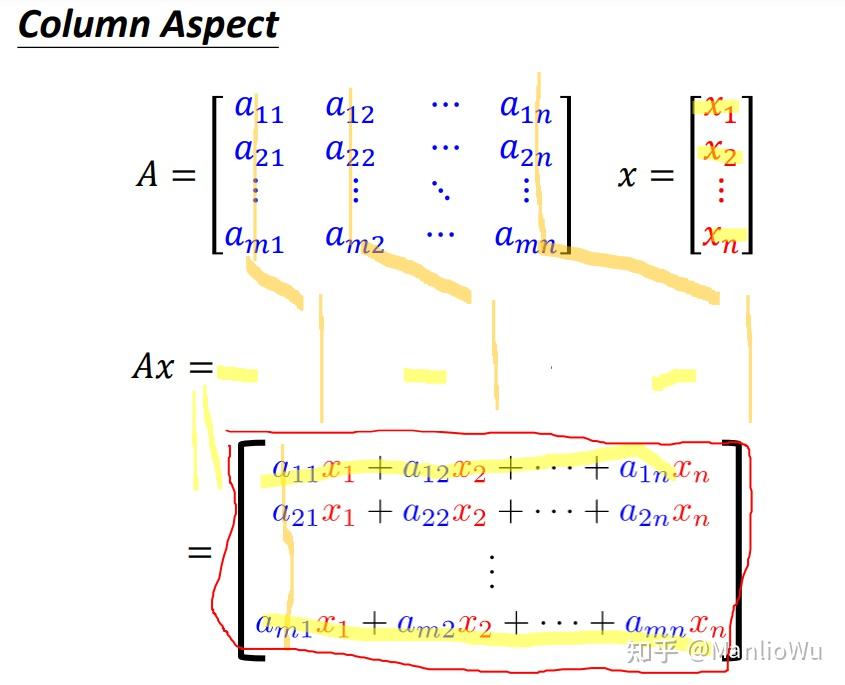
将矩阵 $A$ 视作“列向量的并列”，即每一列均为一个向量。以向量 $x$ 的第 $i$ 个元素乘以矩阵 $A$ 的第 $i$ 个列向量，可得到 $n$ 个向量（若矩阵 $A$ 有 $n$ 列）。将这 $n$ 个向量相加，即得结果 $b$ ，表达式为

$\sum_{i=1}^{n} A_i \ast x_i$

其中， $A_i$ 为列向量， $x_i$ 为标量。此途径同样解释了矩阵列数与向量行数需相等的原因。该技巧可视为对矩阵 $A$ 的 $n$ 将就是个向量进行线性组合以得到新向量，在某些情况下更易于理解。在 3b1b 的线性代数课程中，有一种解释 $A$ 的每个列向量视为向量空间的基向量，向量 $x$ 的每个值为对应基向量的投影长度。将每个投影长度与基向量相乘后再求和，即可得到新向量。

总结与对比

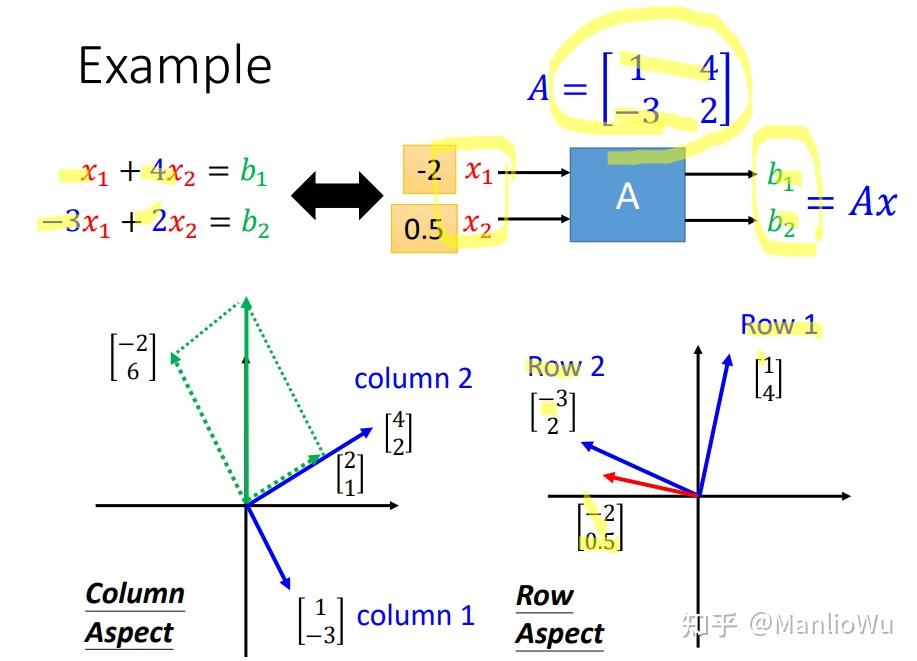
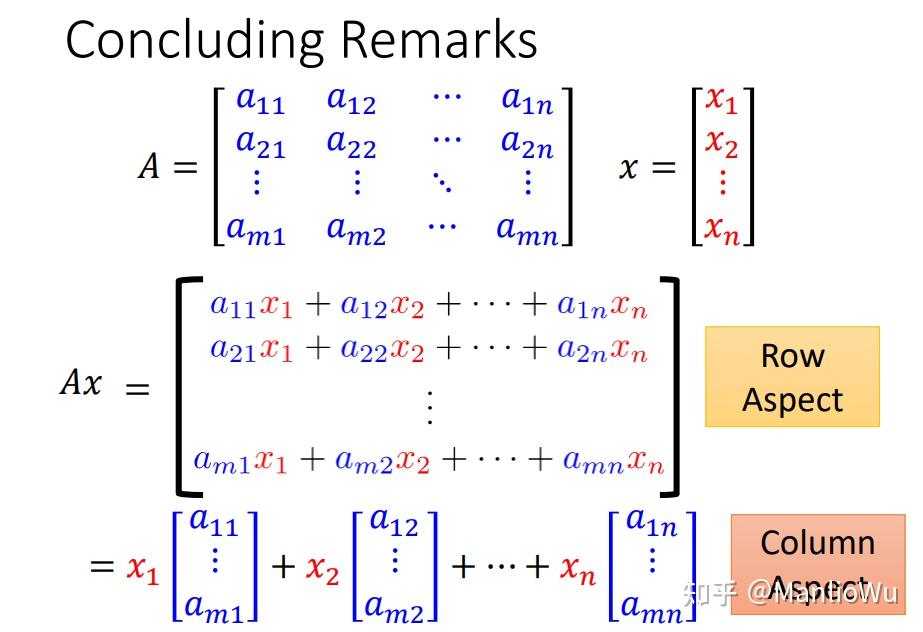
综合来看，列视角（Column Aspect）在理解矩阵与向量相乘方面更具优势，具有重要的现实意义。

发布于 2022-08-04 17:14・广东

矩阵的秩以及行秩 = 列秩的原因

Limi @_zhihu

一个重要概念，广泛应用于多个数学分支。矩阵的秩定义为矩阵中线性无关行向量或列向量的最大数目。具体来说，矩阵就是在矩阵理论中，矩阵的秩 $A$ 的列秩是其线性无关列向量的最大数目，而行秩是其线性无关行向量的最大数目。这两个定义是等价的，即矩阵的秩等于其行秩也等于其列秩。

用数学符号表示，矩阵 $A$ 的秩通常记作 $r (A)$ 、 $\text{rk}(A)$ 或 $\text{rank}\ A$ 。矩阵的秩反映了矩阵中线性无关向量的最大数量，这一数量决定了矩阵的“厚度”或“维度”。

对于矩阵 $A_{m \times n}$ ，可以将其视为由 $n$ 个列向量组成的矩阵。每个列向量对应一个基底，因此极大线性无关组的列向量个数（矩阵的秩）也称为列空间（Column Space）的维度。

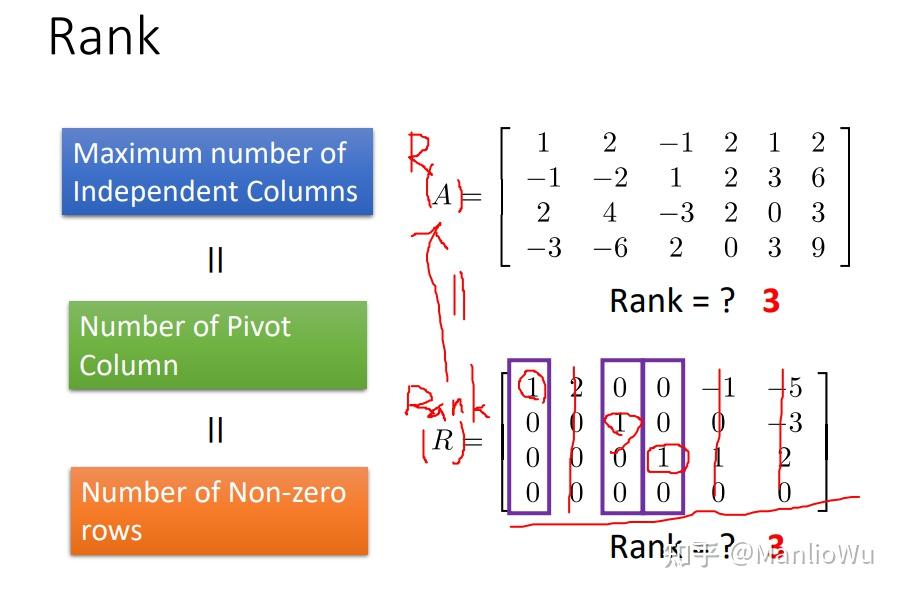
在求解矩阵的秩时，通常通过核心行变换将其转换为阶梯矩阵。在阶梯矩阵中，每一行的第一个非零元素的列数依次向右移动（全零行除外）。即第 $i + 1$ 行的第一个非零元素位于第 $i$ 行第一个非零元素的右下方。矩阵的秩 $r$ 等于阶梯矩阵中单位向量（unit vector）的个数。单位向量是指向量中只有一个元素为 1，其余元素均为 0，也称为基向量（pivot column）或标准向量（standard vector），类似于 one-hot 编码。例如， $[1, 0, 0]$ 和 $[0, 1, 0]$ 均为单位向量。

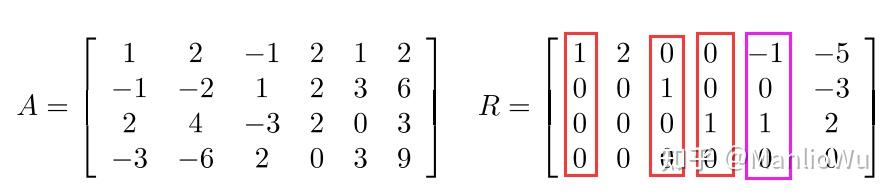
如图所示，左侧为原始矩阵，右侧为阶梯矩阵。阶梯矩阵中有 3 个单位向量（红色框标记），因此列秩为 3。紫色向量为何不能计入矩阵的极大线性无关组呢？因为其非零元素出现的位置并非对应行的第一个，即在其左侧存在单位向量，该向量可由其左侧的单位向量线性表示。例如，图中的矩阵 $\times [1, 0, 0, 0] + 0 \times [0, 1, 0, 0] + 1 \times [0, 0, 1, 0]$ 。线性无关向量组中的向量不能相互表示，因此紫色向量不能计入。

其所在行的第一个非零元素。阶梯矩阵中单位向量的个数即为矩阵的秩。进一步分析可得，“第一个出现的非零元素” 的个数等于非零行的行数，即行秩。因此，矩阵的行秩等于列秩。此外，还可得出就是通过上述例子可知，单位向量的特点是：该向量中 1 的位置 $\text{rank}(A) \leq \min\{m, n\}$ 。

总结如下图：

三种典型的子空间

列空间（Column Space）与行空间（Row Space）与零空间（Null Space）

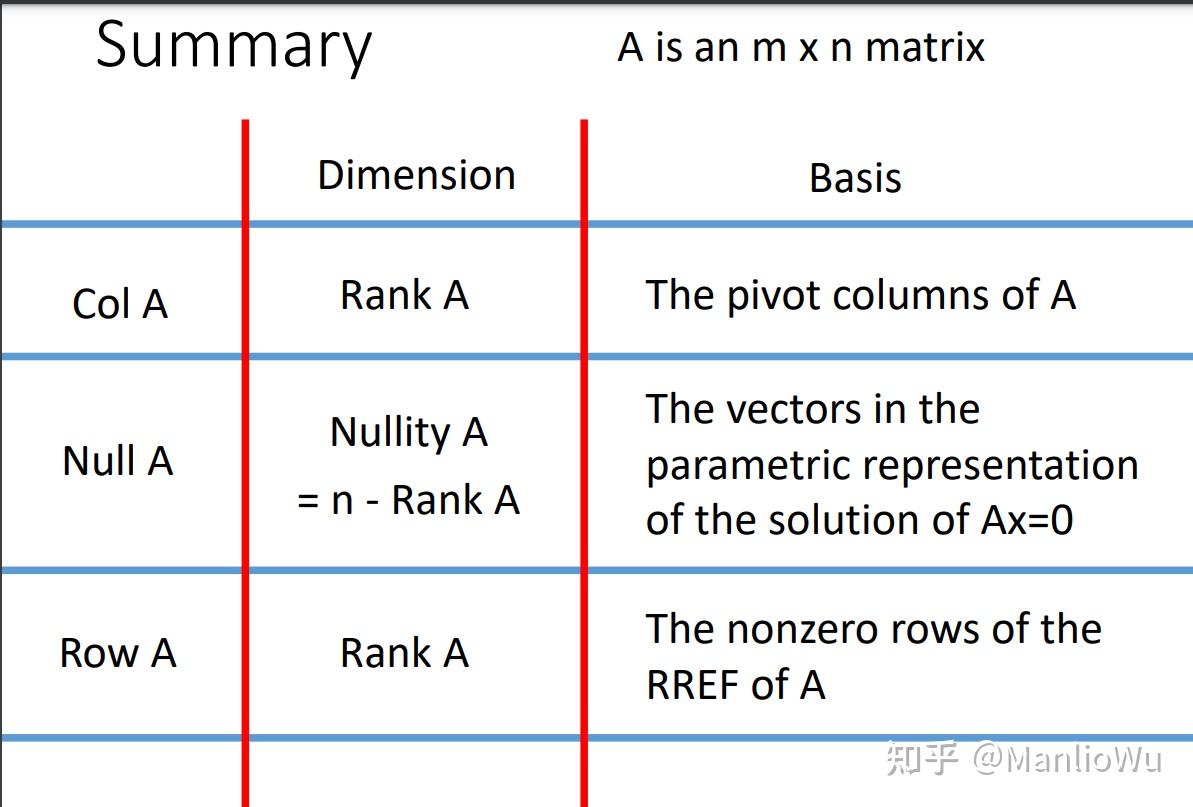
对于零空间（Null Space），即 $A x = 0$ 的基础解系构成的空间。以下是一个例子，其中存在 2 个自由变量（free variable），可得两个基向量（basis），因此零空间的维度为 2。矩阵的秩为 3，满足 $\text{rank}(A) + \text{dimension}(\text{Null space}) = n$ 。

具体分析如下：共有 $n$ 个变量，其中 $k$ 个为自由变量，其余 $n - k$ 个变量可直接确定。在由 $k$ 个自由变量构成的 $k$ 维空间中，任取一个向量，再与 $n - k$ 个确定的值组合，即可得到 $A x = 0$ 的解。从另一个角度理解，存在 $k$ 因为在阶梯矩阵中，有就是个自由变量， $k$ 个列向量可由其余 $n - k$ 个基向量（pivot columns）线性表示。因此，给定一组 $n - k$ 个值，即可求得一组 $k$ 个值。综合所有情况，可形成一个 $k$ 维空间。

单位向量（unit vector）的重要作用

指向量中仅有一个位置为 1，其余位置均为 0。对于就是单位向量 $n$ 维向量，存在 $n$ 个单位向量。按“1” 的位置从小到大排序，分别为 $e_1, e_2, e_3, \dots, e_n$ 。其中， $e_1 = [1, 0, 0, \dots, 0]^T$ ， $e_2 = [0, 1, 0, \dots, 0]$ ， $\dots$ ， $e_n = [0, 0, 0, \dots, 1]^T$ 。

利用这些单位向量可“提取矩阵”。具体而言， $A e_i$ 得到的向量是矩阵 $A$ 的第 $i$ 一个示例：就是列。以下

$\begin{bmatrix} 0 & 1 \\-1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\0 \end{bmatrix}= \begin{bmatrix} 0 \\-1 \end{bmatrix} \quad \begin{bmatrix} 0 & 1 \\-1 & 0 \end{bmatrix} \begin{bmatrix} 0 \\1 \end{bmatrix}= \begin{bmatrix} 1 \\0 \end{bmatrix}$

矩阵与向量相乘可视为向量与其对应投影长度的乘积。单位向量 $e_i$ 仅在第 $i$ 个位置为 1，其余位置为 0，因此只有矩阵 $A$ 的第 $i$ 个列向量的投影长度为 1，其余投影长度为 0，从而可提取矩阵 $A$ 的第 $i$ 列。

编辑于 2022-08-07 20:16

线性代数 —— 矩阵的列秩和行秩

原创于 2019-09-04 19:20:42 发布

1. 矩阵的列秩和行秩及秩的关系（行秩 = 列秩 = 秩）

在这里插入图片描述

2. 初等行变换不改变矩阵的线性相关性

3. 任一矩阵的秩、行秩和列秩相等

4. 求矩阵列向量组的秩及最大无关组示例

via:

矩阵秩的计算方法-CSDN博客
https://blog.csdn.net/edward_zcl/article/details/90177159
矩阵的秩及其求法-CSDN博客
https://blog.csdn.net/qq_55342245/article/details/120188405
什么是矩阵的秩，矩阵的秩如何计算？-CSDN博客
https://blog.csdn.net/weixin_44114030/article/details/143424474
从两个角度看矩阵和向量相乘 - 知乎
https://zhuanlan.zhihu.com/p/549884913
矩阵的秩以及为什么行秩=列秩 - 知乎
https://zhuanlan.zhihu.com/p/550019600
线性代数学习笔记——矩阵的列秩和行秩_行秩和列秩怎么求-CSDN博客
https://blog.csdn.net/hpdlzu80100/article/details/100545450

posted @ 2025-09-17 15:49 wzzkaifa 阅读(237) 评论(0) 收藏举报

刷新页面返回顶部

wzzkaifa