完整教程:【数据结构入门】排序算法(3):详解快速排序
作为最强排序,一定要给一个排面,所以单独做一期博客,来讲讲最强排序——快速排序。
目录
1.单趟排序思路
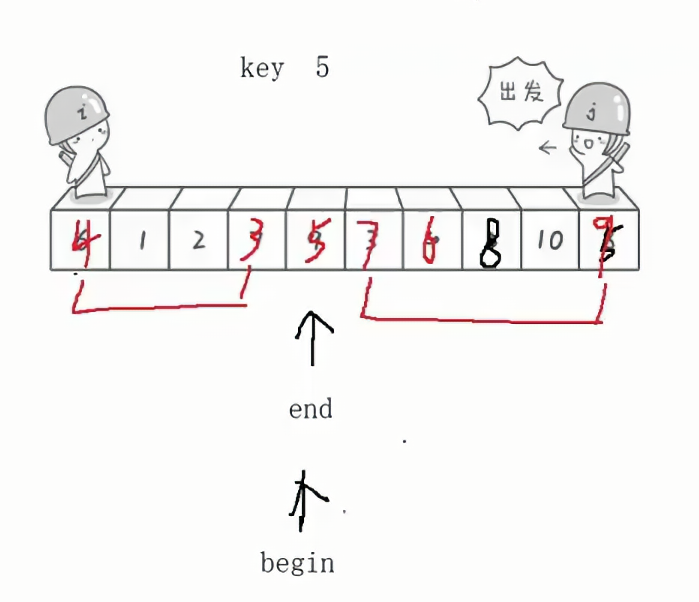
首先将最后一个数字作为key,指定两个指针,begin和end,begin的使命是找到一个比key大的数,end的使命是找到一个比key小的数,如果此时begin和end没有相遇,那么就将begin和end指向的值进行交换。
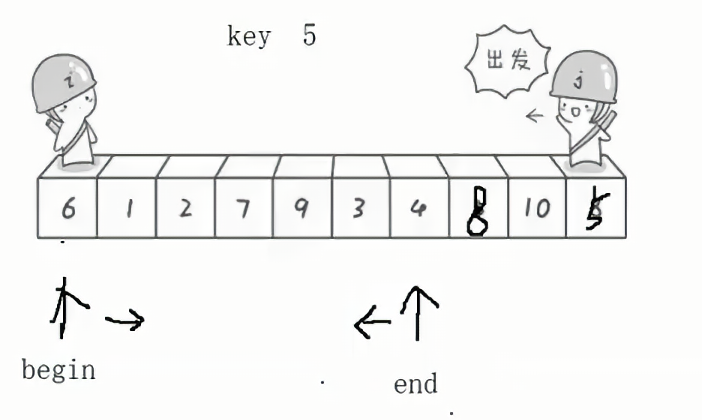
如下图所示:
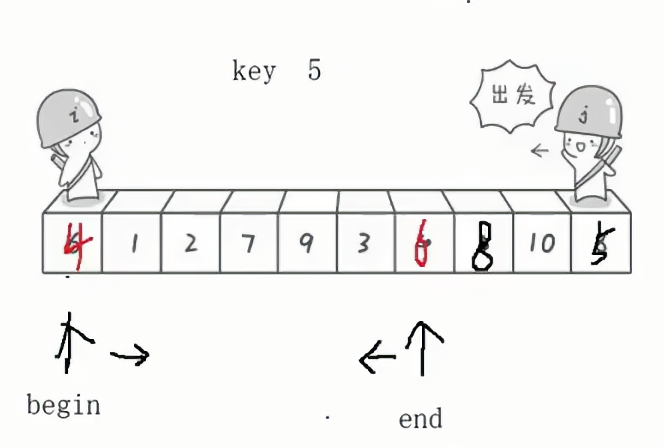
剩下的同理,3、7进行交换:
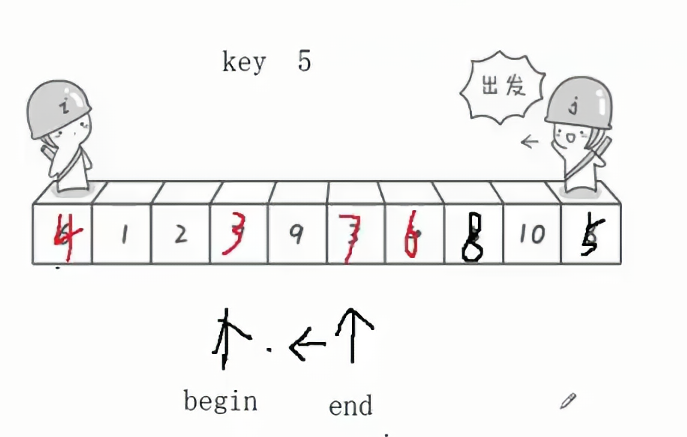
如果此时end和begin指针相遇,那么此时判断指针所指的值比key要大,所以最后将key和指针指向的值进行交换,如下图所示:9和5进行交换。
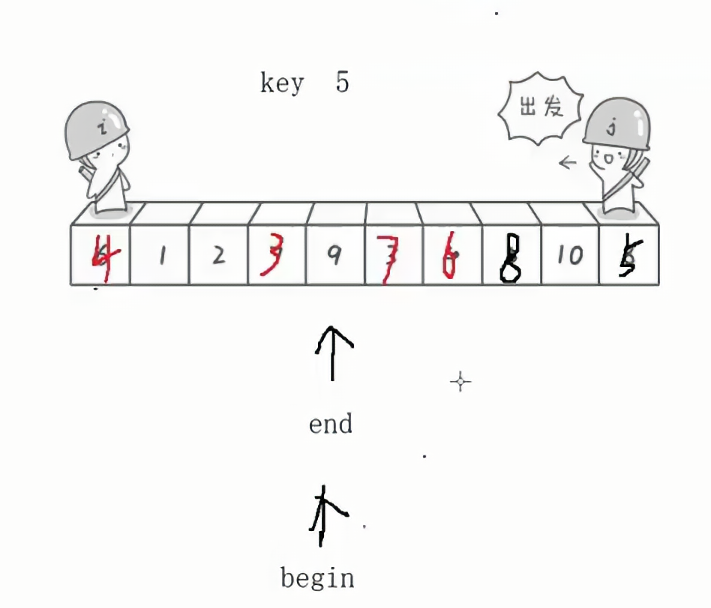
最后的结果就是,将整个数组被key分成了两个部分,key的左边部分是比key小,key的右边部分是比key大,中间是key。此时key这个值不需要再变动了,key已经来到了该来的位置。
2.单趟排序的代码
2.1 左右指针法
2.1.1 思路
首先单趟排序的形参必须有三个参数:数组、起始下标、最后一个元素的下标,这样一来排序的区间就是闭区间[begin,end];
最外层循环退出的条件是当begin > end的时候;进入循环之后,首先判断begin如果是小于指定的key,那么begin++,因为begin的本质就是找大值;同理end如果大于key,就key++,因为key本身就是找小值;
如果begin和end同时停下来,说明begin找到比key大的值,end找到比key小的值,此时直接交换;
需要注意的是:也有可能出现下面这种情况,在判断的过程中,如果当end出现在begin的左边,此时进行的交换是无效的。
2.1.2 选key的门道
如果选择最右边的数字为key,那么就让begin先走;同理如果选择最左边的数字为key,那么就让end先走;总结就是选择哪一边作为key,就让另外一边先走。如此一来,才能实现让key的左边都是比它小的数字,右边都是比它大的数字。
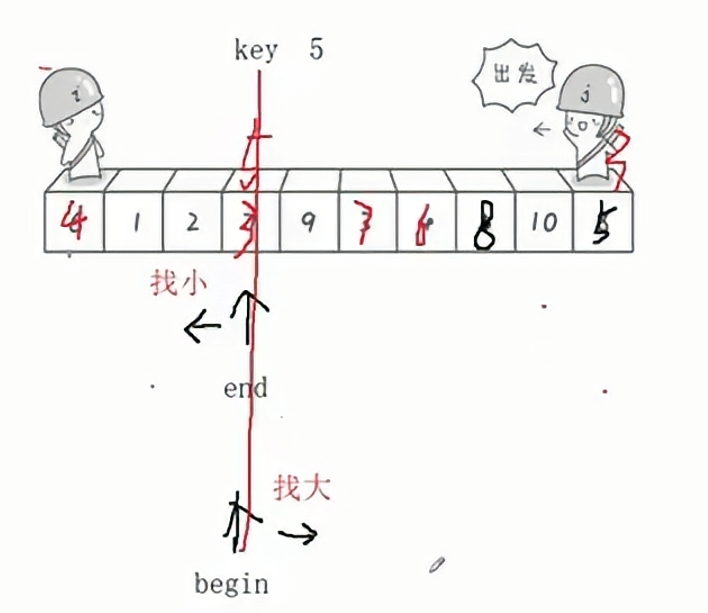
如上图所示,让最右边的5作为key,那么先让end先走,begin再走,这样就会在3的位置相遇,那么最后将key和相遇位置交换,就会出现问题,相遇位置比key小,所以就不满足key的右边比key大这一规律。
如果我们想要保持这一规律,那么就需要让begin先走,end再走,此时不论是左边遇右边,还是右遇左,此时相遇的地方都是比key大的,此时再进行交换就能满足要求。
2.1.3 代码
需要注意的是,如果begin和end此时和key相等,还是需要移动下标,否则会进入死循环。
// 单趟快速排序
int one_sort(int* arr, int begin, int end)
{
// [begin,end] 令end为key
int key = arr[end];
int key_pos = end;
// 此时要让begin先走
while (begin = key && begin < end) // end找小,找不到就左移
{
--end;
}
// 相遇的地方一定是比key要大的值
Swap(&arr[begin], &arr[end]);
}
// 相遇退出循环
/*
此时相遇的地方一定比key要大,最后一次交换
*/
Swap(&arr[begin], &arr[key_pos]);
return begin; // 此时[0,begin] key [begin,最后]
}2.2 挖坑法
2.2.1 思路
首先需要将最右边(8)作为key,然后将8挖掉,随机使用begin指针来找到比8大的数,然后填入key的坑,9填入key的坑之后,9本身会形成一个坑;
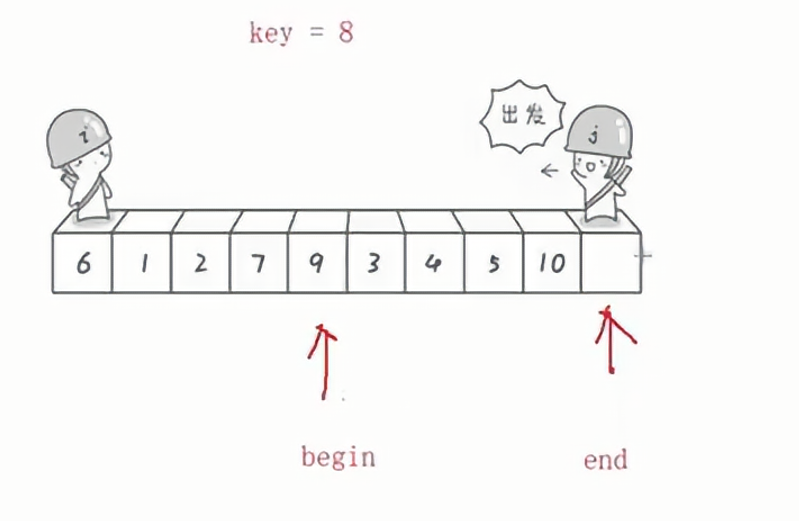
此时再用end指针找小,找到一个小于key的值,再填入9所在的坑,下图是end找到了5填入begin的坑;
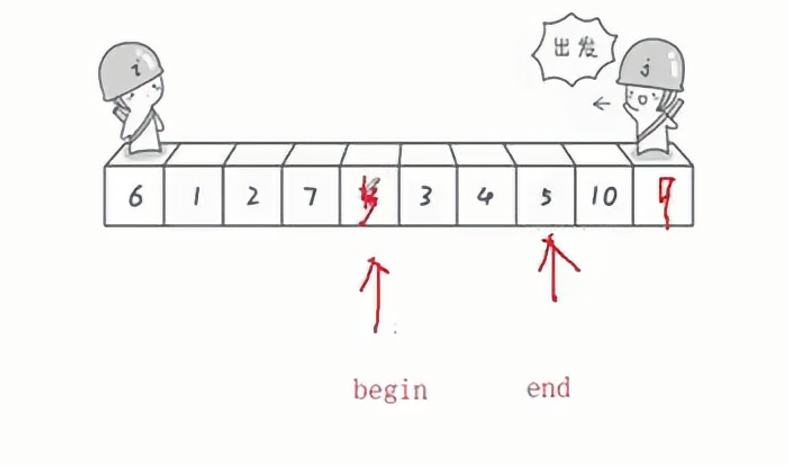
后面继续使用begin来找大于key的值,继续填入5之前的位置(坑)......
2.2.2 代码
// 挖坑法
int dig_hole(int* a,int begin,int end)
{
int mid_index = get_midIndex(a, begin, end);
Swap(&a[end],&a[mid_index]); // 确保key不是最大或最小值
int key = a[end];
// end是第一个坑
while (begin = key)
{
--end;
}
// 将这个值填入新坑
a[begin] = a[end];
}
// end和begin相遇了
a[begin] = key;
return begin;
}2.3 前后指针法
2.3.1 思路
使用两个指针,prev和curr,如果curr找到比key小的数,那么prev就++,并且交换curr所指向的值。
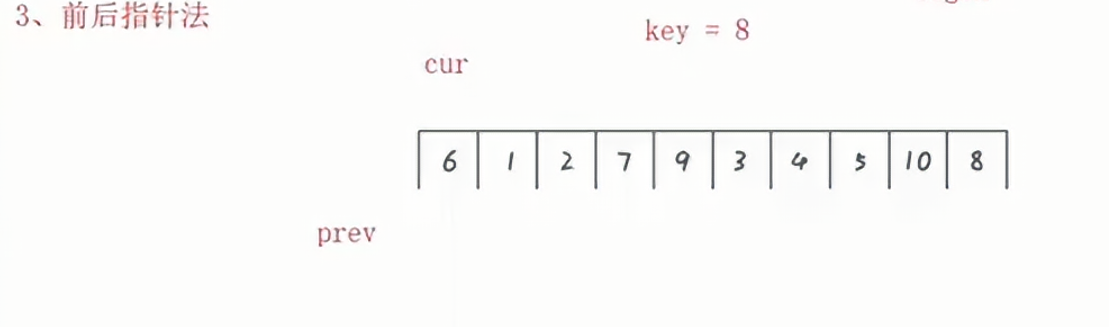
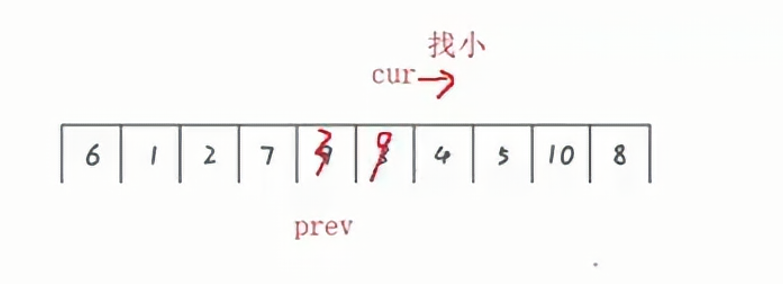
prev始终比curr要小,当curr指向空的时候,此时循环结束,将key和prev进行交换即可。
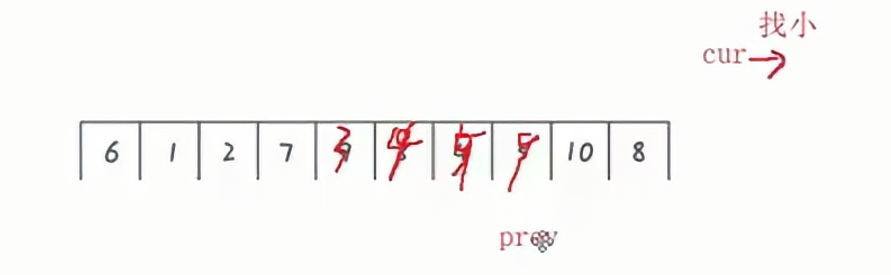
本质上就是curr不断找小的数,将小的数放在前面,将大的数向后推。
2.3.2 代码
// 前后指针法
int two_pointer(int* arr, int begin, int end)
{
// curr找小
int curr = begin;
int prev = begin - 1;
int key = arr[end];
while (curr < end) // 不处理最后一个数字(key)
{
// 找到了比key小的数
if (arr[curr] <= key && curr != ++prev) // 并且prev+1之后不为curr,自己和自己就不用交换
{
Swap(&arr[curr], &arr[prev]);
}
++curr; // 没找到或者交换完毕curr都需要++
}
// 退出循环,之后先++prev,再把prev和key交换
Swap(&arr[++prev], &arr[end]);
return prev;
}3.多趟排序思路
上面我们提到了,如何将一个数字变得有序,情况如下,当一个数字变得有序的时候,这个数据的左边是比它小的数,右边是比它大的数,此时分别递归左右两边的数组,就能完成所有数字的有序。
以此类推,区间就会不断缩小,当且仅递归到当key的左右两段数组只有一个值或没有值的时候,此时数组是有序的,那么再进行回溯,此时小数组有序,那么大数组的一部分也变得有序了。
3.1 最差时间复杂度
此时数组是有序的或者接近有序的,每次都选最后一个作为key,此时每次递归数组元素的个数变成了等差数列,时间复杂度是O(N²)。
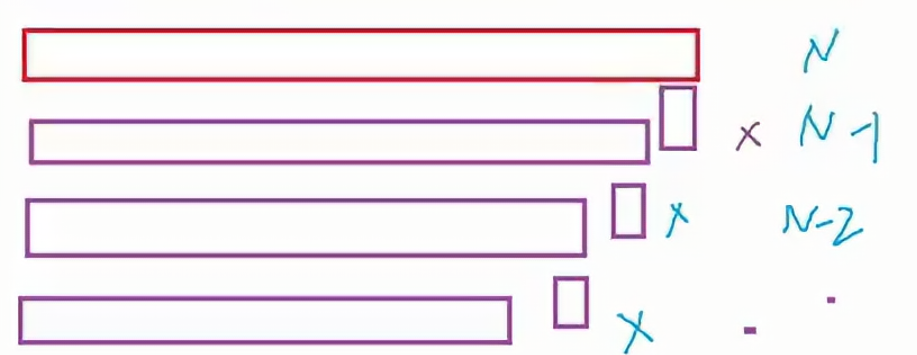
3.2 最优时间复杂度
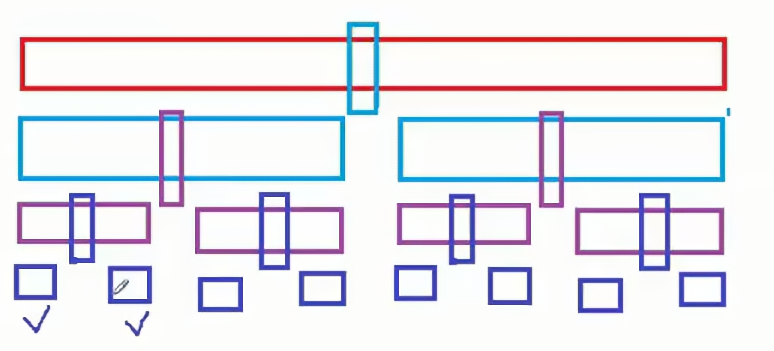
上图画的是一种理想情况,实际情况key的选择不可能每次恰好是最中间的那个(即中位数),所以当key是三个数中的最小值或者最大值的时候,如果左右子数组是有序或者是没有值的时候,此时也是正常排序;
第一层需要遍历N次,第二层,除开选出的key,需要遍历N-1次,那么可以当做N次,以此类推,每层遍历N次;将此图转换成二叉树那么,二叉树的高度就是logN;每一层需要遍历N次,那么时间复杂度就是:
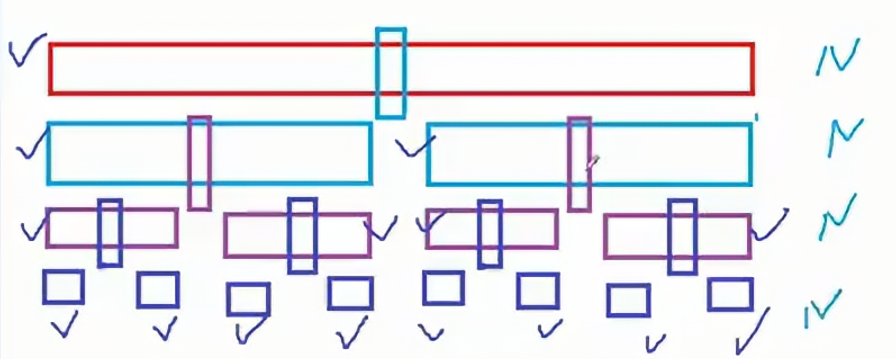
所以每次选择的key值越接近中位数,那么排序的效率就会越高,如果数组接近有序或者有序那么排序的效率就会退化成N²。
3.3 多趟排序的代码
具体思路就是递归,上面的图是一种特殊情况,每一次的key刚好在最中间,将一段区域划分成多个区域,最后如果出现[num_index,num_index]的时候,说明就剩一个数了,无需排序,直接退出递归。
这里递归退出的条件是,begin > end,此时的区间是无效的,begin == end的时候,区间只有一个数字了,就无需排序了。
// 快速排序
/*
[begin,end]
当begin >= end就返回
*/
void quick_sort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
// 先第一步划分
int middle_pos = one_sort(arr, begin, end);
// 左边递归
quick_sort(arr, begin, middle_pos - 1);
// 右边递归
quick_sort(arr, middle_pos + 1, end);
}4. 快排的优化
4.1 时间复杂度退化
快速排序的劣势在于,如果排序数组是一个有序或者接近有序的数组,那么此时会退化时间复杂度为O(N²),因为我们每一次选择key是最左或者最右边的数字,那么一定是最大或者最小的数字。为了避免这种情况我们可以:
选择key的时候需要保证key不是最大的也不是最小的即可。
我们只需要写一个方法,这个方法能够选出三个数中居中的数的下标,知道了这个数的下标,我们就可以将这个数作为key,这样就能保证,key一定不是最大或者最小的数。
如果是最坏的情况,即整个数组是有序的,那么这样就可以每次取到中间值,也就是将最坏情况逆转为最好情况;
如果是随机情况,不一定会有大的优化。所以此次优化是针对于最坏情况,能够让最坏情况扭转为最好情况。所以此时不存在O(N²)的时间复杂度,最后综合的时间复杂度是:
// 三个数选择中间那个数的下标
int get_midIndex(int* arr,int begin,int end)
{
int mid = (begin + end) / 2;
if (arr[begin] arr[end]) // end mid
if (arr[mid] > arr[end]) // begin > mid > end
{
return mid;
}
else if (arr[end] > arr[begin]) // end > begin > mid
{
return begin;
}
else
{
return end;// begin > end > mid
}
}
}4.2 区间较小时避免递归滥用
假如区间内只有10个数,那么还是需要不断递归,那么可以选择其他排序进行替代,这里可以选择插入排序。大于10个数使用快排,小于10个数使用插入排序。
// 快速排序
/*
[begin,end]
当begin >= end就返回
*/
void quick_sort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end - begin + 1 > 10)
{
// 先第一步划分
int middle_pos = two_pointer(arr, begin, end);
// 左边递归
quick_sort(arr, begin, middle_pos - 1);
// 右边递归
quick_sort(arr, middle_pos + 1, end);
}
else
{
insert_sort(arr + begin,end - begin + 1); // 区间内
}
}5.快排的完整代码
#define _CRT_SECURE_NO_WARNINGS
#include
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
// 三个数选择中间那个数的下标
int get_midIndex(int* arr, int begin, int end)
{
int mid = (begin + end) / 2;
if (arr[begin] arr[end]) // end mid
if (arr[mid] > arr[end]) // begin > mid > end
{
return mid;
}
else if (arr[end] > arr[begin]) // end > begin > mid
{
return begin;
}
else
{
return end;// begin > end > mid
}
}
}
// 单趟快速排序
int one_sort(int* arr, int begin, int end)
{
// 选择一个左中右里居中的数字,这样就可以避免快排出现最坏情况
int midIndex = get_midIndex(arr, begin, end);
Swap(&arr[midIndex], &arr[end]);// 让这个数字作为key
// [begin,end] 令end为key
int key = arr[end];
int key_pos = end;
// 此时要让begin先走
while (begin = key && begin = key)
{
--end;
}
// 将这个值填入新坑
a[begin] = a[end];
}
// end和begin相遇了
a[begin] = key;
return begin;
}
// 前后指针法
int two_pointer(int* arr, int begin, int end)
{
// curr找小
int curr = begin;
int prev = begin - 1;
int key = arr[end];
while (curr = 0)
{
if (tmp = end就返回
*/
void quick_sort(int* arr, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end - begin + 1 > 10)
{
// 先第一步划分
int middle_pos = two_pointer(arr, begin, end);
// 左边递归
quick_sort(arr, begin, middle_pos - 1);
// 右边递归
quick_sort(arr, middle_pos + 1, end);
}
else
{
insert_sort(arr + begin,end - begin + 1); // 区间内
}
}
int main()
{
int arr[] = { 3,1,4,1,7,9,8,2,0,5 };
int size = sizeof(arr) / sizeof(arr[0]);
quick_sort(arr, 0, size - 1);
for (int i = 0; i < size; ++i)
{
printf("%d ", arr[i]);
}
return 0;
}6. 使用栈来实现快排
快排一旦使用递归,那么递归就可以被改写成用栈来实现,我们来实现一下。
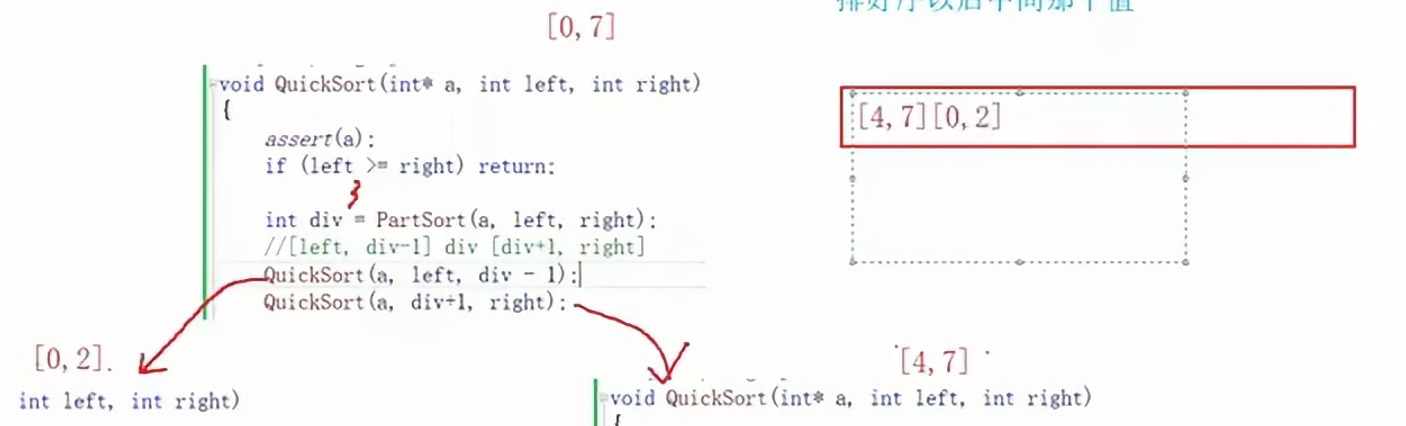
此时我们需要排0-7,此时先入栈,找到mid,将区间氛围两部分,分别对两部分进行排序,排序前先出栈;
如果我们先要排0-2,那么就先入栈4-7,再入栈0-2,这样0-2就会先出栈,即先排序。
0-2出栈之后,就会将0-2划分为0-0,2-2(mid=1),先对0-0排序那么就让2-2先入栈,再让0-0入栈如下图:

0-0和2-2都是一个数,不需要排序,所以直接出栈就好了,最后取出4-7出栈,4-7被划分为4-4和6-7,如果先处理4-4,那么需要先让6-7入栈,再让4-4入栈;4-4已经有序,直接弹出即可,最后处理6-7,分为6-5和7-7,由于6-5是非法区间所以不需要入栈,就剩一个7-7,已经有序了。

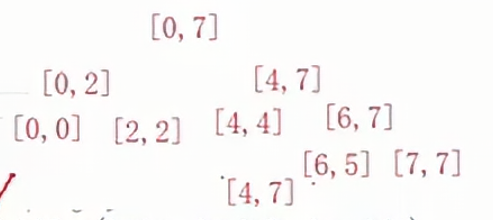
这里需要用到之前写过的栈结构;
①首先需要创建栈,然后将当前区域的右边界、左边界依次入栈(顺序无所谓,这里先处理左);
②进入循环,如果循环条件(栈不为空),那么就满足条件,首先对左右边界进行求中间的元素的index;
③将区间分为:begin 到 mid-1,mid,mid+1到end,此时如果要先处理左区域,那么就需要先将右区域入栈,再将左区域入栈。
④循环往复,第二次循环其实就是针对上一个大区间的左区间,使用单趟排序使得左区间变得逐渐有序。
⑤第三次循环针对上一个大区间的右区间,使用单趟排序使得右区间逐渐变得有序。
⑥每一次循环将区间变得越来越小,将小区间变得有序,直到栈为空,说明所有区间已经全部处理完毕(因为[0.0],[5,4],不会入栈)。
6.1 代码
// 使用栈来实现快排
void quick_sort_stack(int* arr, int begin, int end)
{
Stack stk;
InitStack(&stk);
// 先入右再入左,那么就是先处理左
PushStack(&stk, end);
PushStack(&stk, begin);
// 栈不为空那么就继续
while (!isEmpty(&stk))
{
int begin = getTop(&stk); // 先入的是右,先出的是左
PopStack(&stk);
int end = getTop(&stk);
PopStack(&stk);
// 算出mid
int mid = one_sort(arr, begin, end);
// 先处理左边界,所以先push右边界
// 此时被分为三个区域
if (mid + 1 < end)// 如果是右边区域
{
// 入区间的时候也是一样,先处理左端点那么就先入右端点
PushStack(&stk, end);// [mid+1,end]
PushStack(&stk, mid + 1);
}
// 再push左边界
if (begin < mid - 1)
{
PushStack(&stk, mid - 1);
PushStack(&stk, begin);
}
}
DestroyStack(&stk);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号