机器学习（4）：正则化 - 详解

1. 正则化(Regularization)

1. 过拟合

过拟合指机器学习模型在训练数据上表现完美，但在新内容（测试数据）上表现很差的现象。

• 原因：机器没有学习到数据背后的规律，而是把训练数据中的特例、噪声甚至随机波动都当成了规律来学习，导致模型变得过于麻烦和专门化，失去了泛化到新数据的能力。

• 对策：

  • 舍弃无关特征，或对某些特征进行算法处理（降维、聚类等）

  • 减少参数的大小就是正则化：保留所有的特征，但

1. 正则化

1. 核心思想：凭借向模型的损失函数添加一个“惩罚项”，来限制模型的复杂度，从而防止过拟合。

2. 数学公式：

• 没有正则化的目标：最小化损失函数 Minimize(Loss)

• 有正则化的目标：最小化 【损失函数 + λ * 惩罚项】，即 Minimize(Loss + λ * Penalty)

  • 惩罚项 (Penalty)：通常与模型权重参数（w）的大小直接相关。权重越大，惩罚项越大。它惩罚那些“特别大”的权重值。

    • 权重值大，意味着模型非常“看重”对应的那个特征，即使该特征发生微小的变化，也会导致输出的巨大波动,这通常是模型拟合了噪声和异常点的标志。

    • 通过限制权重值的大小，模型会变得更平滑、更稳定，泛化能力更强。

  • λ (Lambda)：正则化强度，是一个超参数。它控制你有多重视“保持模型简单”该目标。

    • λ = 0：正则化失效，退回到原模型。

    • λ → 非常大：模型会变得非常非常简单（比如所有权重趋近于0），可能导致欠拟合。

    • 我们需要选择一个合适的 λ，在“拟合训练数据”和“保持模型简单”之间找到最佳平衡。

1. 正则化类型：

特性对比维度	L2正则化 (岭回归, Ridge)	L1正则化 (套索回归, Lasso)
核心思想	惩罚大的权重，使所有特征系数都均匀变小，但不消除任何特征。	惩罚权重的绝对值，倾向于将不重要的特征系数完全压缩至零。
目标函数示例	Minimize( Loss + λ * ∑wᵢ² )	Minimize( Loss + λ * ∑\|wᵢ\| )
解的性质	非稀疏解 (Non-sparse)	稀疏解 (Sparse)
权重趋势	权重渐进地趋近于0，但永远不会等于0。	产生精确的0值权重，从而完全忽略某些特征。
核心能力	抑制模型复杂度，防止过拟合，提高模型稳定性。	自动进行特征选择，生成更简单、可解释性更强的模型。
几何约束形状	圆形（2D） / 球体（高维）	菱形（2D） / 菱形体（高维）
计算与优化	惩罚项可微，易于进行基于梯度下降的优化。	惩罚项在0点不可微，需使用次梯度等特殊方法优化。
典型适用场景	当资料中存在大量特征，且你认为所有特征都可能与结果相关时。	当你认为许多特征是无关或冗余的，并希望得到一个简洁的模型时

• L2正则化（岭回归）

  • 核心思想：通过惩罚模型权重的平方大小，来限制模型的复杂度。它致力于让所有特征的权重都变得“小一点”，避免任何单一特征对预测结果产生过大的影响，使模型更加稳定和平滑。

  • 数学公式：优化后的目标函数为：

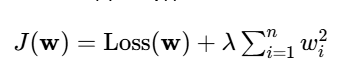
• 特点：

  • 收缩效应：随着 λ增大，所有权重都会被均匀地收缩，趋近于零但永远不会真正等于零。

  • 保留所有特征：即使某个特征不核心，它的权重也只会变得很小，而不会被完全移除。因此，最终模型会含有所有输入特征。

  • 稳定性：对于资料中的微小扰动（噪声）不敏感，模型方差更低，泛化能力更强。

• 适用范围：

  • 数据特征：当资料中存在大量特征，且这些特征都对因变量有影响（只是重要性不同）

  • 主要目的：防止过拟合，提高模型的泛化能力，而不关心特征选择。

• L1正则化（套索回归）

  • 核心思想：通过惩罚模型权重（系数）的绝对值大小，来限制模型的复杂度。它不仅致力于降低权重，更拥有一种“选择”能力，可能将不重要特征的权重彻底设置为零。

  • 数学公式：优化后的目标函数为：

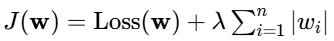
• • 特点：

    • 稀疏化效应：这是Lasso最核心的特点。随着λ增大，它会将不重要特征的权重精确地压缩至零。

    • 特征选择：由于会产生稀疏权重向量，Lasso本质上完成了一次特征选择。最终模型只保留那些对预测目标最重要的特征，模型变得非常简单和可解释。

  • 适用范围：

    • 素材特征：数据中许多特征是完全无关、冗余或共线性的

    • 关键目的：自动进行特征选择，得到一个更简单、更易于解释的模型。