实用指南：深度学习之第三课PyTorch（ MNIST 手写数字识别神经网络模型）

MNIST 数据集作为深度学习入门的 “Hello World”，包含 70000 张 28×28 像素的手写数字灰度图像（60000 张训练集 + 10000 张测试集），任务目标是准确识别图像中的数字（0-9）。本节课将以该数据集为载体，手把手教您运用 PyTorch 实现核心步骤：首先，学习如何使用 PyTorch 的torchvision库加载并预处理 MNIST 数据，包括数据标准化、批量加载等关键操作，为模型训练做好数据准备；其次，详细讲解神经网络的搭建逻辑，从定义包含输入层、隐藏层、输出层的全连接网络结构，到选择合适的激活函数（如 ReLU）和损失函数（交叉熵损失），让您理解每一层的作用与参数设计思路；接着，深入模型训练流程，涵盖优化器（如 SGD、Adam）的配置、训练循环的编写（前向传播计算预测值、反向传播更新参数），以及如何监控训练过程中的损失变化与准确率提升；最后，学习使用测试集评估模型性能，分析模型在 unseen 数据上的泛化能力，并通过实际案例演示模型的预测过程，直观感受手写数字识别的效果。

一、PyTorch框架认识

1. Tensor张量

在PyTorch中，张量（Tensor）是核心数据结构，它是一个多维数组，用于存储和变换数据。张量类似于Numpy中的数组，但具有更丰富的功能和灵活性，特别是在支持GPU加速方面。

定义与特性
        多维数组：张量可以看作是一个n维数组，其中n可以是任意正整数。它可以是标量（零维数组）、向量（一维数组）、矩阵（二维数组）或具有更高维度的数组。
        数据类型统一：张量中的元素具有相同的数据类型，这有助于在GPU上进行高效的并行计算。
        支持GPU加速：PyTorch中的张量可以存储在CPU或GPU上，通过将张量转移到GPU上，可以利用GPU的强大计算能力来加速深度学习模型的训练和推理过程。
创建方式
        直接使用torch.tensor()：根据提供的Python列表或Numpy数组创建张量。
        下载数据集时：transform=ToTensor()直接将数据转化为Tensor张量类型。

2.自动求导（Autograd）

# 定义一个 tensor，并设置 requires_grad=True
x = torch.ones(2, 2, requires_grad=True)
print(x)
# 定义一个简单运算
y = x + 2
z = y * y * 3
out = z.mean()
# 反向传播计算梯度
out.backward()
print(x.grad)

注意：计算图在反向传播后默认会释放，如果需要多次反向传播，需要设置 retain_graph=True。

3.构建神经网络（nn模块）

nn.Module：所有神经网络模型都需要继承该类。(下面有具体的构建方法)

层级组合：可以将多层组合在一起，形成更复杂的网络结构。

二、MNIST 手写数字识别

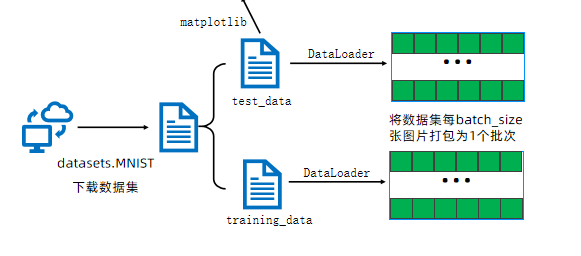
对于mnist数据集的数据照片如下图，我将详细说明每一步都内容

1.导入必要的库

import torch
from torch import nn
from torch.utils.data import DataLoader
from torchvision import datasets
from torchvision.transforms import ToTensor

torch：PyTorch 的主库，提供了张量操作和深度学习的基本功能
nn：神经网络模块，包含了各种层和损失函数
DataLoader：用于数据加载和批处理的工具
datasets：包含了常用的数据集，这里使用 MNIST
ToTensor：将图片转换为 PyTorch 张量的转换工具

2. 加载 MNIST 数据集

# 下载训练集
train_data = datasets.MNIST(
root='data',#数据集的根目录，下载位置
train=True, #如果为True，则从training.pt创建数据集，否则从test.pt创建数据集
download=True,# 为True，则从internet下载数据集放入根目录，如果已经下载好不会重复下载
transform=ToTensor(),# 接收PIL图片并返回转换后版本图片的转换函数
)
# 下载测试集
test_data = datasets.MNIST(
root='data',
train=False,          # 加载测试集
download=True,
transform=ToTensor(),
)

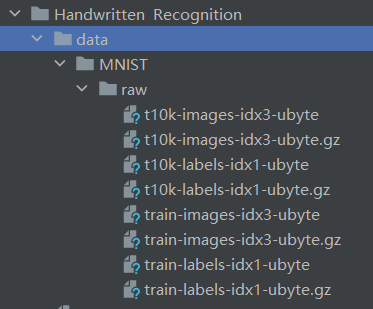
MNIST 是一个经典的手写数字数据集，包含 60,000 个训练样本和 10,000 个测试样本，每个样本是 28×28 像素的灰度图像，标签是 0-9 的数字。当你本地没有MNIST数据集的时候，download会给你在代码目录下载数据。

3. 数据可视化

from matplotlib import pyplot as plt
figure = plt.figure()
for i in range(9):
img, label = train_data[i]
figure.add_subplot(3, 3, i+1)
plt.title(label)
plt.axis("off")
plt.imshow(img.squeeze(), cmap='gray')
plt.show()

这段代码展示了训练集中的前 9 张图片及其对应的标签，img.squeeze()用于去除张量中维度为 1 的维度（从 [1,28,28] 变为 [28,28]）。

4. 数据加载器

train_dataloader = DataLoader(train_data, batch_size=64)
test_dataloader = DataLoader(test_data, batch_size=64)

DataLoader的作用是：

将数据分成批次（batch_size=64 表示每批 64 个样本）
可以打乱数据顺序（默认不打乱，可通过 shuffle=True 设置）
支持多线程加载数据

下面的代码验证了数据的形状：

for x, y in test_dataloader:
print(f"shape of x [n,c,h,w]: {x.shape}")  # 输出: [64, 1, 28, 28]
print(f"shape of y: {y.shape} {y.dtype}") # 输出: [64] torch.int64
break

x 的形状：[批次大小，通道数，高度，宽度]
y 的形状：[批次大小]，存储每个样本的标签

5. 设备配置

device = "cuda" if torch.cuda.is_available() else 'mps' if torch.backends.mps.is_available() else 'cpu'
print(f"use {device}")

这段代码自动选择可用的计算设备：

优先使用 NVIDIA GPU (cuda)
其次使用 Apple M 系列芯片的 GPU (mps)
最后使用 CPU

6. 构建神经网络模型

class MauralNetwork(nn.Module):  # 注意：类名应该是NeuralNetwork，这里可能是笔误
def __init__(self):
super().__init__()
self.Flatten = nn.Flatten()  # 将二维图像展平为一维向量
self.hidden1 = nn.Linear(28*28, 128)  # 第一个全连接层
self.hidden2 = nn.Linear(128, 256)    # 第二个全连接层
self.out = nn.Linear(256, 10)         # 输出层，10个类别
def forward(self, x):
x = self.Flatten(x)          # 展平: [batch, 1, 28, 28] -> [batch, 784]
x = self.hidden1(x)          # 第一层线性变换
x = torch.sigmoid(x)         # 激活函数
x = self.hidden2(x)          # 第二层线性变换
x = torch.sigmoid(x)         # 激活函数
x = self.out(x)              # 输出层
return x
model = MauralNetwork().to(device)  # 将模型移动到选定的设备
print(model)

关于这样的模型我们就搭建完成

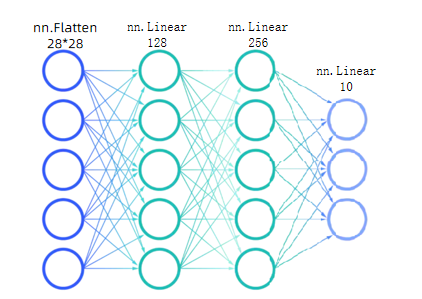
这是一个简单的多层感知机 (MLP)：

神经网络组件：

输入层：784 个神经元（28×28）
隐藏层 1：128 个神经元，使用 sigmoid 激活函数
隐藏层 2：256 个神经元，使用 sigmoid 激活函数
输出层：10 个神经元（对应 0-9 数字）
- nn.Module：所有神经网络模块的基类
- nn.Linear：全连接层
- nn.Flatten：将多维张量展平
- 激活函数：如sigmoid，增加模型的非线性能力

最后还有我们需要使用的损失函数和优化器，这里使用的优化器是梯度下降，

loss_fn = nn.CrossEntropyLoss()  # 交叉熵损失函数，适用于分类问题
optimizer = torch.optim.SGD(model.parameters(), lr=0.2)  # 随机梯度下降优化器

CrossEntropyLoss：结合了 softmax 和 NLLLoss，是分类问题的常用损失函数
SGD：随机梯度下降优化器，lr=0.2是学习率

1. 损失函数（Loss Function）：衡量预测与真实的差距

损失函数（也称为代价函数或目标函数）的核心作用是量化模型预测结果与真实标签之间的差异。它输出一个非负值（损失值），值越小表示模型预测越接近真实情况。

2. 优化器（Optimizer）：调整参数以减小损失

优化器的核心作用是根据损失函数的梯度，调整模型参数（如权重和偏置），从而最小化损失函数。它决定了模型如何 "学习"—— 即如何从错误中修正参数。

两者的协同工作流程

前向传播：模型使用当前参数对输入数据进行预测。
计算损失：通过损失函数，比较预测结果与真实标签，得到损失值。
反向传播：计算损失函数对每个参数的梯度（即参数变化对损失的影响程度）。
参数更新：优化器根据梯度信息，调整参数（如减小权重或偏置），以降低下一次的损失。

7. 训练和测试函数

训练函数

def train(dataloader, model, loss_fn, optimizer):
model.train()  # 设置模型为训练模式
batch_size_num = 1
for x, y in dataloader:
x, y = x.to(device), y.to(device)  # 将数据移动到设备
# 前向传播
pred = model.forward(x)
loss = loss_fn(pred, y)
# 反向传播和优化
optimizer.zero_grad()  # 清空梯度
loss.backward()        # 反向传播计算梯度
optimizer.step()       # 更新模型参数
loss = loss.item()
if batch_size_num % 400 == 0:
print(f"loss: {loss:>7f} [number: {batch_size_num}]")
batch_size_num += 1

训练过程的核心步骤：

前向传播：计算模型预测
计算损失：衡量预测与真实标签的差距
反向传播：计算损失对各参数的梯度
参数更新：根据梯度调整参数

测试函数

def test(dataloader, model, loss_fn):
size = len(dataloader.dataset)
num_batches = len(dataloader)
model.eval()  # 设置模型为评估模式
test_loss, correct = 0, 0
with torch.no_grad():  # 关闭梯度计算，节省内存和计算资源
for x, y in dataloader:
x, y = x.to(device), y.to(device)
pred = model.forward(x)
test_loss += loss_fn(pred, y).item()
# 计算正确预测的数量
correct += (pred.argmax(1) == y).type(torch.float).sum().item()
test_loss /= num_batches  # 平均损失
correct /= size           # 准确率
print(f"Test result:\n Accuracy: {(100*correct)}%, Avg loss: {test_loss}")

测试过程不更新模型参数，主要用于评估模型性能：

计算测试集上的平均损失
计算准确率（正确预测的样本比例）

如果到这里我们的模型和数据都已经处理好了，是可以进行训练预测得到结果了，但是经过我们训练发现,我们训练的效果非常低,这是为什么呢?

这是因为我们首先把数据传入模型进行前向传播,模型的参数都是随机生成的,任何也就进行一次都梯度下降进行反向传播寻找不到最佳的参数,我们我们要去增加多轮的训练才行.

8.多轮模型训练

epochs = 10  # 训练轮次
for t in range(epochs):
print(f"Epoch {t+1}\n...............")
train(train_dataloader, model, loss_fn, optimizer)
print("结束")
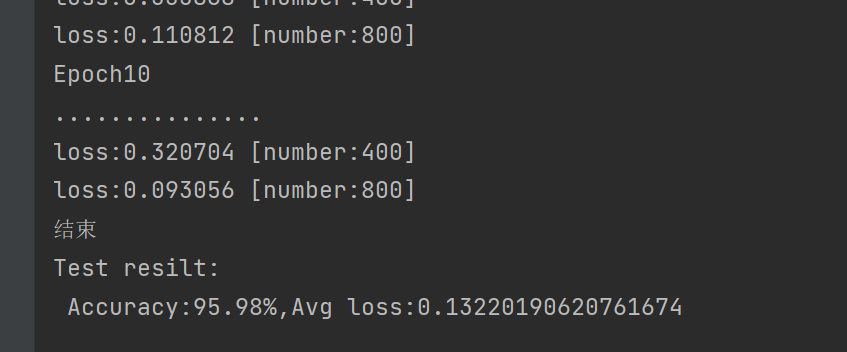
test(test_dataloader, model, loss_fn)

epochs=10：表示整个训练集会被模型学习 10 次

我们发现经过10轮而已准确率就很不错了（这里是因为我训练过最佳参数了95%是比较高的了），而损失函数也很低（读者可以多进行几轮训练效果会更好）

三、模型优化

对于模型我们还没有提到优化器以及损失函数的选择问题，选择合适的优化器和损失函数可以大大提高模型店准确率。

也就是这两行代码

loss_fn = nn.CrossEntropyLoss()  # 交叉熵损失函数，适用于分类问题
optimizer = torch.optim.SGD(model.parameters(), lr=0.2)  # 随机梯度下降优化器

CrossEntropyLoss：结合了 softmax 和 NLLLoss，是分类问题的常用损失函数
SGD：随机梯度下降优化器，lr=0.2是学习率

1. 损失函数（Loss Function）

衡量预测与真实的差距

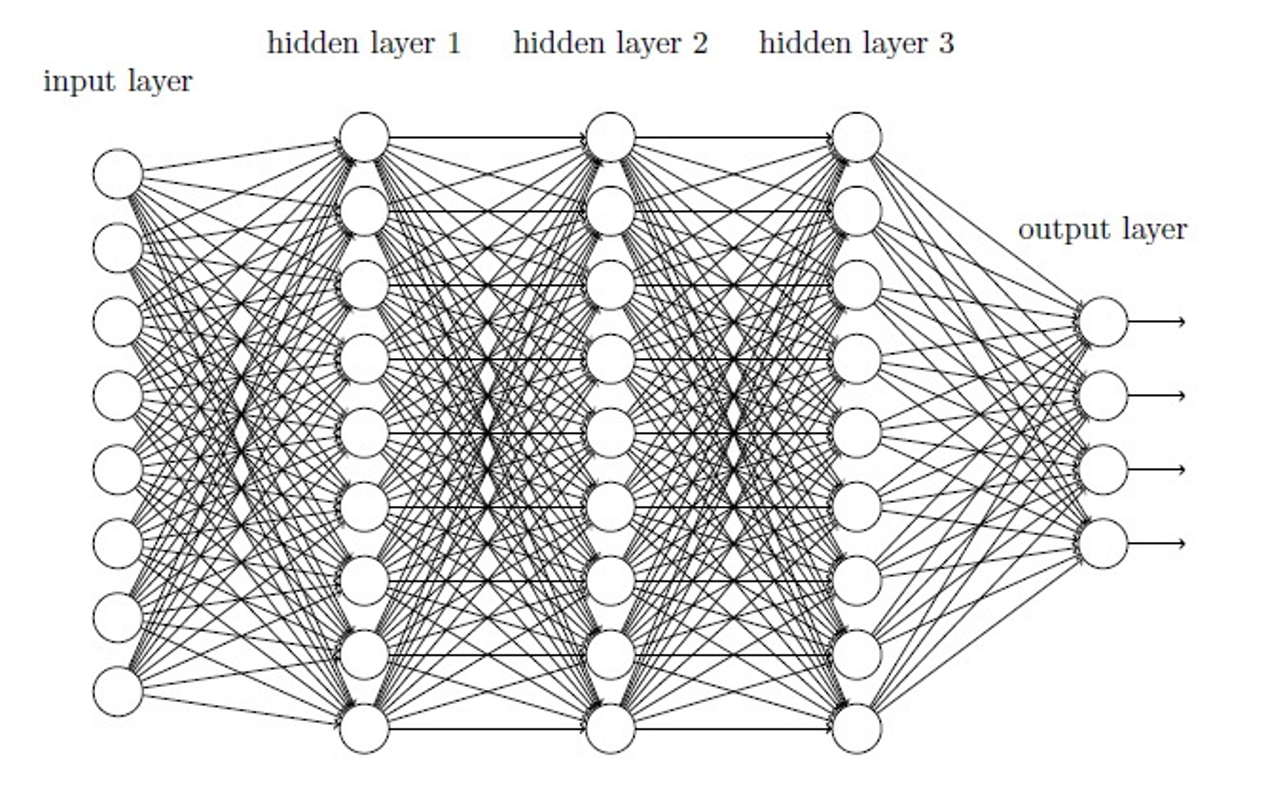
对于三层及以上的神经网络，sigmiod函数可能会产生梯度消失或者梯度爆炸问题，

梯度消失

如果连乘的因子大部分小于1，最后乘积的结果可能趋于0，也就是梯度消失，后面的网络层的参数不发生变化.

梯度爆炸

如果连乘的因子大部分大于1，最后乘积可能趋于无穷，这就是梯度爆炸

造成原因：

梯度反向传播中的连乘效应。对于更普遍的梯度消失问题，可以考虑以下方案解决：用ReLU、tanh、P-ReLU、R-ReLU、Maxout等替代sigmoid函数。

【ReLU】：如果激活函数的导数是1，那么就没有梯度爆炸问题了

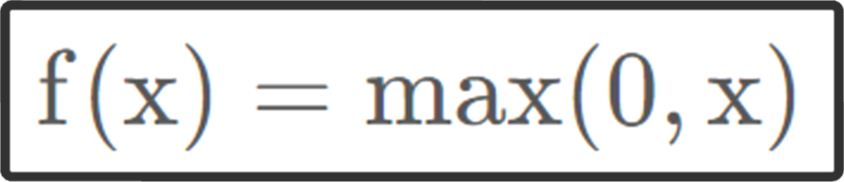
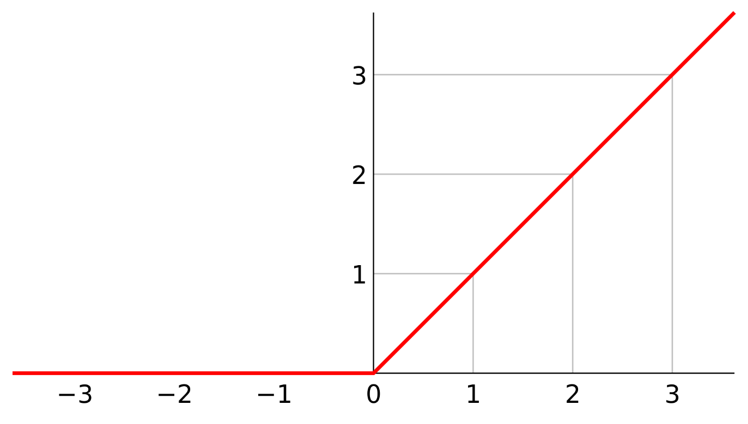
2. 优化器（Optimizer）

调整参数以减小损失

批量梯度下降法（Batch Gradient Descent）

使用全样本数据计算梯度，例如一个batch_size=64，计算出64个梯度值

好处：收敛次数少。坏处：每次迭代需要用到所有数据，占用内存大耗时大

随机梯度下降法（Stochastic Gradient）

从64个样本中随机抽出一组，训练后按梯度更新一次

优点：速度快。缺点：可能陷入局部最优，搜索起来比较盲目，并不是每次都朝着最优的方向

小批量梯度下降法（Mini-batch Gradient）

将训练数据集分成小批量用于计算模型误差和更新模型参数。是批量梯度下降法和随机梯度下降法的结合。

还有：

自适应矩估计(Adaptive Moment Estimation) Adam
动量梯度下降（Momentum Gradient Descent）
AdaGrad
RMSprop
AdamW
Adadelta