数学学习 | 计算机科学中的数学应用 - 教程

注：本文为 “数学学习” 相关合辑。

中文引文，略作重排。
英文引文，机翻未校。
如有内容异常，请看原文。

---

计算机科学中的数学应用概要

本文从计算机专业学生的视角出发，深入探讨了数学体系及其在计算机科学中的应用。

作者从集合论这一现代数学的共同基础讲起，阐述了分析和代数两大数学家族的发展脉络。

在分析部分，从微积分的古典时代讲到实分析、拓扑学、微分几何等现代分支，重点介绍了极限、实数理论、测度理论等核心概念及其在现代分析中的重要性。

在代数部分，从抽象代数的基本概念讲到线性代数、泛函分析、李群和李代数等，强调了代数结构在数学和计算机科学中的应用。

最后，文章还简要介绍了现代概率论在分析基础上的发展及其在金融、随机过程等领域的应用。展示了数学从基础理论到高级应用的逐步深入，以及数学在计算机科学中的重要性和实用性。

---

MIT 牛人解说数学体系

5 月 18th, 2010
Posted by P.Linux | Filed

为什么要深入数学的世界

对 appearance 和 motion 建立一个 unified 的 model。这个题目在当今 Computer Vision 中百花齐放的世界中并没有任何特别的地方。事实上，使用各种 Graphical Model 把各种东西联合在一起 framework，在近年的论文中并不少见。就是作为计算机的学生，我没有任何企图要成为一个数学家。我学习数学的目的，是想爬上巨人的肩膀，希望站在更高的高度，能把我自己研究的东西看得更深广一些。说起来，我在刚来这个学校的时候，并没有预料到我将会有一个深入数学的旅程。我的导师最初希望我去做的题目，

通过大量“原子”的某种空间分布构成的，原子群的运动形成了动态的可视过程。微观意义下的单个原子运动，和宏观意义下的整体分布的变换存在着深刻的联系——这得我们去发掘。就是我不否认现在广泛流行的 Graphical Model 是对复杂现象建模的有力设备，但是，我认为它不是 panacea，并不能取代对于所研究的问题的深入的钻研。如果统计学习包治百病，那么很多“下游”的学科也就没有存在的必要了。事实上，开始的时候，我也是和 Vision 中很多人一样，想着去做一个 Graphical Model——我的导师指出，这样的做法只是重复一些标准的流程，并没有很大的价值。经过很长时间的反复，另外一个路径慢慢被确立下来——我们相信，一个图像

在深入探索这个题目的过程中，遇到了很多很多的疑问，如何描述一个一般的运动过程，如何建立一个稳定并且广泛适用的原子表达，如何刻画微观运动和宏观分布变换的联系，还有很多。在这个过程中，我发现了两个事情：

• 我原有的数学基础已经远远不能适应我对这些问题的深入研究。
• 在数学中，有很多思想和工具，是非常适合解决这些问题的，只是没有被很多的应用科学的研究者重视。

于是，我决心开始深入数学这个浩瀚大海，希望在我再次走出来的时候，我已经有了更强大的武器去面对这些问题的挑战。

我的游历并没有结束，我的视野相比于这个博大精深的世界的依旧显得非常狭窄。在这里，我只是说说，在我的眼中，数学如何一步步从初级向高级发展，更高级别的数学对于具体应用究竟有何好处。

集合论：现代数学的共同基础

现代数学有数不清的分支，但是，它们都有一个共同的基础——集合论——因为 它，数学该庞大的家族有个共同的语言。集合论中有一些最基本的概念：集合 (set)，关系 (relation)，函数 (function)，等价 (equivalence)，是在其它数学分支的语言中几乎必然存在的。对于这些简单概念的理解，是进一步学些别的数学的基础。我相信，理工科大学生对于这些都不会陌生。

_
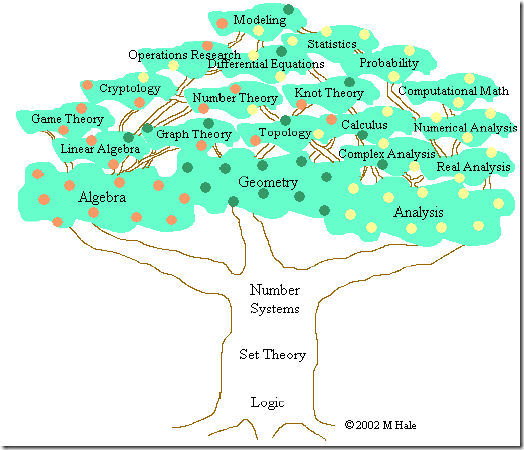
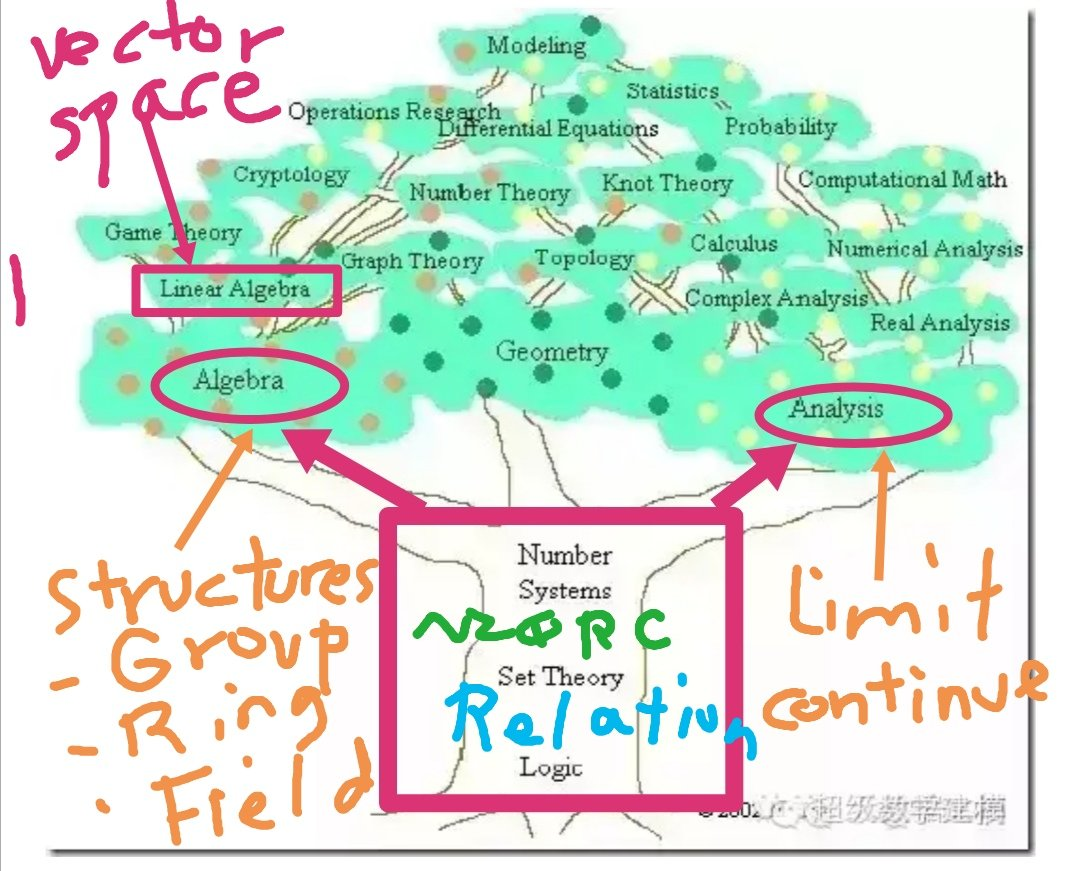
Modern Math Foundation : Set + Logic (Equivalence Relation).
现代数学基础：集合 + 逻辑（等价关系）。

A level (H2 level) / International Baccalauréat Math should study the big red square box (Number System, Set Theory, Logic).
A水平（H2水平）/国际文凭数学课程应当学习红色大方框内的内容（数系、集合论、逻辑学）。

All STEM university Year 1 & 2 study these 3 Math foundations :Algebra, Analysis & Vector Space.
所有 STEM 专业的大学一二年级学生都会学习这三大数学基础：代数学、分析学和向量空间。

The Math major university Year 3&4 study more : real /complex analysis, Topology, Galois Theory, graph theory, etc…
大学三四年级的数学专业学生则会学习更多内容：实分析/复分析、拓扑学、伽罗瓦理论、图论等等……

不过，有一个很重要的东西就不见得那么家喻户晓了——那就是“选择公理” (Axiom of Choice)。这个公理的意思是“任意的一群非空集合，一定许可从每个集合中各拿出一个元素。”——似乎是显然得不能再显然的命题。不过，这个貌似平常的公理却能演绎出一些比较奇怪的结论，比如巴拿赫 - 塔斯基分球定理——“一个球，能分成五个部分，对它们进行一系列刚性变换（平移旋转）后，能组合成两个一样大小基础接受的，由于很多数学分支的重要定理都依赖于它。在我们后面要回说到的学科里面，下面的定理依赖于选择公理：就是的球”。正基于这些完全有悖常识的结论，导致数学界曾经在相当长时间里对于是否接受它有着激烈争论。现在，主流数学家对于它应该

1. 拓扑学：Baire Category Theorem
2. 实分析（测度理论）：Lebesgue 不可测集的存在性
3. 泛函分析四个主要定理：Hahn-Banach Extension Theorem, Banach-Steinhaus Theorem (Uniform boundedness principle), Open Mapping Theorem, Closed Graph Theorem

在集合论的基础上，现代数学有两大家族：分析 (Analysis) 和代数 (Algebra)。平行的关系。就是至于其它的，比如几何和概率论，在古典数学时代，它们是和代数并列的，但它们的现代版本则基本是建立在分析或者代数的基础上，因此从现代意义说，它们和分析与代数并不

分析：在极限基础上建立的宏伟大厦

微积分：分析的古典时代——从牛顿到柯西

先说说分析 (Analysis) 吧，它是从微积分 (Calculus) 发展起来的——这也是有些微积分教材名字叫“数学分析”的原因。不过，分析的范畴远不止这些，我们在大学一年级学习的微积分只能算是对古典分析的入门。分析研究的对象很多，包括导数 (derivatives)，积分 (integral)，微分方程 (differential equation)，还有级数 (infinite series)——这些基本的概念，在初等的微积分里面都有介绍。如果说有一个思想贯穿其中，那就是极限——这是整个分析（不仅仅是微积分）的灵魂。

一个很多人都听说过的故事，就是牛顿 (Newton) 和莱布尼茨 (Leibniz) 关于微积分发明权的争论。事实上，在他们的时代，很多微积分的工具开始运用在科学和工程之中，只是，微积分的基础并没有真正建立。那个长时间一直解释不清楚的“无穷小量”的幽灵，困扰了数学界一百多年的时间——这就是“第二次数学危机”。直到柯西用数列极限的观点重新建立了微积分的基本概念，这门学科才开始有了一个比较坚实的基础。直到今天，整个分析的大厦还是建立在极限的基石之上。

，这样的结果并不令人满意，工程师们需对分段连续函数的函数积分。就是柯西 (Cauchy) 为分析的发展提供了一种严密的语言，但是他并没有解决微积分的全部疑问。在 19 世纪的时候，分析的世界仍然有着一些挥之不去的乌云。而其中最重要的一个没有解决的是“函数是否可积的困难”。我们在现在的微积分课本中学到的那种通过“无限分割区间，取矩阵面积和的极限”的积分，是大约在 1850 年由黎曼 (Riemann) 提出的，叫做黎曼积分。但是，什么函数存在黎曼积分呢（黎曼可积）？数学家们很早就证明了，定义在闭区间内的连续函数是黎曼可积的。可

实分析：在实数理论和测度理论上建立起现代分析

在 19 世纪中后期，不连续函数的可积性问题一直是分析的重要课题。对于定义在闭区间上的黎曼积分的研究发现，可积性的关键在于“不连续的点足够少”。只有有限处不连续的函数是可积的，可是很多有数学家们构造出很多在无限处不连续的可积函数。显然，在衡量点集大小的时候，有限和无限并不是一种合适的标准。在探讨“点集大小”这个问题的过程中，数学家发现实数轴——这个他们曾经以为已经充分理解的东西——有着许多他们没有想到的特性。在极限思想的支持下，实数理论在这个时候被建立起来，它的标志是对实数完备性进行刻画的几条等价的定理（确界定理，区间套定理，柯西收敛定理，Bolzano-Weierstrass Theorem 和 Heine-Borel Theorem 等等）——这些定理明确表达出实数和有理数的根本区别：完备性（很不严格的说，就是对极限运算封闭）。随着对实数认识的深入，如何测量“点集大小”的问题也取得了突破，勒贝格创造性地把关于集合的代数，和 Outer content（就是“外测度”的一个雏形）的概念结合起来，建立了测度理论 (Measure Theory)，并且进一步建立了以测度为基础的积分——勒贝格 (Lebesgue Integral)。在这个新的积分概念的支持下，可积性问题变得一目了然。

上面说到的实数理论，测度理论和勒贝格积分，构成了我们现在称为实分析 (Real Analysis) 的数学分支，有些书也叫实变函数论。对于应用科学来说，实分析似乎没有古典微积分那么“实用”——很难直接基于它得到什么算法。而且，它要解决的某些“难题”——比如处处不连续的函数，或者处处连续而处处不可微的函数——在工程师的眼中，并不现实。然而，我认为，它并不是一种纯数学概念游戏，它的现实意义在于为许多现代的应用数学分支提供坚实的基础。下面，我仅仅列举几条它的用处：

1. 黎曼可积的函数空间不是完备的，但是勒贝格可积的函数空间是完备的。轻松地说，一个黎曼可积的函数列收敛到的那个函数不一定是黎曼可积的，可是勒贝格可积的函数列必定收敛到一个勒贝格可积的函数。在泛函分析，还有逼近理论中，时常需要讨论“函数的极限”，或者“函数的级数”，如果用黎曼积分的概念，这种讨论几乎不可想像。我们有时看一些 paper 中提到$L^p$函数空间，就是基于勒贝格积分。
2. 总能绕过去。就是勒贝格积分是傅立叶变换（这东西在工程中到处都是）的基础。很多关于信号处理的初等教材，可能绕过了勒贝格积分，直接讲点面对实用的东西而不谈它的数学基础，但是，对于深层次的研究问题——特别是希望在理论中能做一些工作——这并不
3. 现代概率论的基础。就是在下面，我们还会看到，测度理论

拓扑学：分析从实数轴推广到一般空间——现代分析的抽象基础

随着实数理论的建立，大家开始把极限和连续推广到更一般的地方的分析。事实上，很多基于实数的概念和定理并不是实数特有的。很多特性行抽象出来，推广到更一般的空间里面。对于实数轴的推广，促成了点集拓扑学 (Point-set Topology) 的建立。很多原来只存在于实数中的概念，被提取出来，进行一般性的讨论。在拓扑学里面，有 4 个 C 构成了它的核心：

1. Closed set（闭集合）。在现代的拓扑学的公理化体系中，开集和闭集是最基本的概念。一切从此引申。这两个概念是开区间和闭区间的推广，它们的根本地位，并不是一开始就被认识到的。经过相当长的时间，人们才认识到：开集的概念是连续性的基础，而闭集对极限运算封闭——而极限正是分析的根基。
2. 保持极限运算的函数”——比如就是Continuous function（连续函数）。连续函数在微积分里面有个用 epsilon-delta 语言给出的定义，在拓扑学中它的定义是“开集的原像是开集的函数”。第二个定义和第一个是等价的，只是用更抽象的语言进行了改写。我个人认为，它的第三个（等价）定义才从根本上揭示连续函数的本质——“连续函数$y$ 是数列 $x_1,x_2,x_3,\dots$的极限，那么如果$f$是连续函数，那么$f(y)$ 就是 $f(x_1),f(x_2),f(x_3),\dots$相当的。就是的极限。连续函数的重要性，可以从别的分支学科中进行类比。比如群论中，基础的运算是“乘法”，对于群，最要紧的映射叫“同态映射”——保持“乘法”的映射。在分析中，基础运算是“极限”，因此连续函数在分析中的地位，和同态映射在代数中的地位
3. Connected set（连通集合）。比它略为窄一点的概念叫 (Path connected)，就是集合中任意两点都存在连续路径相连——可能是一般人理解的概念。一般意义下的连通概念稍微抽象一些。在我看来，连通性有两个重要的用场：一个是用于证明一般的中值定理 (Intermediate Value Theorem)，还有就是代数拓扑，拓扑群论和李群论中讨论根本群 (Fundamental Group) 的阶。
4. 它的另一种形式——“紧集中的数列必存在收敛子列”——它体现了分析中最重要的“极限”。Compactness 在现代分析中运用极广，无法尽述。微积分中的两个重要定理：极值定理 (Extreme Value Theorem)，和一致收敛定理 (Uniform Convergence Theorem) 就可能借助它推广到一般的形式。就是Compact set（紧集）。Compactness 似乎在初等微积分里面没有专门出现，不过有几条实数上的定理和它其实是有关系的。比如，“有界数列必然存在收敛子列”——用 compactness 的语言来说就是——“实数空间中有界闭集是紧的”。它在拓扑学中的一般定义是一个听上去比较抽象的东西——“紧集的任意开覆盖存在有限子覆盖”。这个定义在讨论拓扑学的定理时很方便，它在很多时候能帮助实现从无限到有限的转换。对于分析来说，用得更多的

从某种意义上说，点集拓扑学可以看成是关于“极限”的一般理论，它抽象于实数理论，它的概念成为几乎所有现代分析学科的通用语言，也是整个现代分析的根基所在。

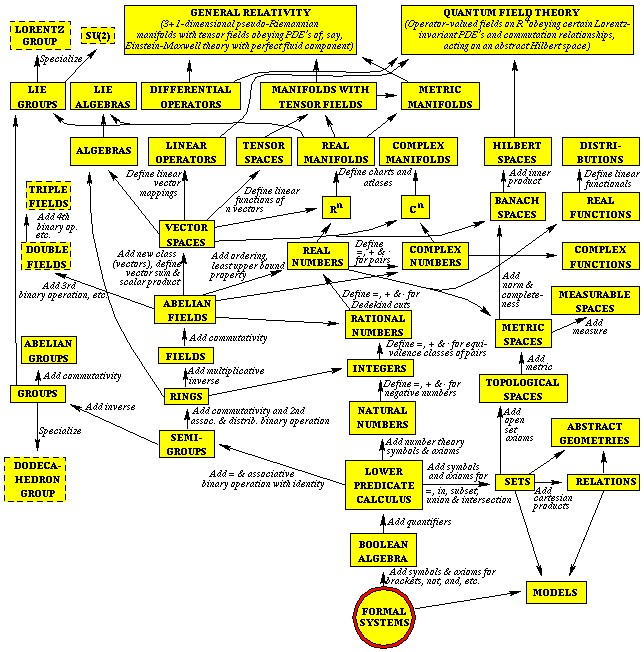
微分几何：流形上的分析——在拓扑空间上引入微分结构

拓扑学把极限的概念推广到一般的拓扑空间，但这不是故事的结束，而仅仅是开始。在微积分里面，极限之后大家有微分，求导，积分。这些东西也可以推广到拓扑空间，在拓扑学的基础上建立起来——这就是微分几何。从教学上说，微分几何的教材，有两种不同的类型，一种是建立在古典微积分的基础上的“古典微分几何”，主要是关于二维和三维空间中的一些几何量的计算，比如曲率。还有一种是建立在现代拓扑学的基础上，这里姑且称为“现代微分几何”——它的核心概念就是“流形”(manifold)——就是在拓扑空间的基础上加了一套可以进行微分运算的结构。现代微分几何是一门非常丰富的学科。比如一般流形上的微分的定义就比传统的微分丰富，我自己就见过三种从不同角度给出的等价定义——这一方面让事情变得复杂一些，但是另外一个方面它给了同一个概念的不同理解，往往在解决问题时会引出不同的思路。除了推广微积分的概念以外，还引入了很多新概念：tangent space, cotangent space, push forward, pull back, fibre bundle, flow, immersion, submersion 等等。

近些年，流形在 machine learning 似乎相当时髦。但是，坦率地说，要弄懂一些根本的流形算法，甚至“创造”一些流形算法，并不需要多少微分几何的基础。对我的研究来说，微分几何最重要的应用就是建立在它之上的另外一个分支：李群和李代数——这是数学中两大家族分析和代数的一个漂亮的联姻。分析和代数的另外一处重要的结合则是泛函分析，以及在其基础上的调和分析。

代数：一个抽象的世界

关于抽象代数

回过头来，再说说另一个大家族——代数。

如果说古典微积分是分析的入门，那么现代代数的入门点则是两个部分：线性代数 (linear algebra) 和基础的抽象代数 (abstract algebra)——据说国内一些教材称之为近世代数。

代数——名称上研究的似乎是数，在我看来，主要研究的是运算规则。一门代数，其实都是从某种具体的运算体系中抽象出一些基本规则，建立一个公理体系，然后在这基础上进行研究。一个集合再加上一套运算规则，就构成一个代数结构。在关键的代数结构中，最简单的是群 (Group)——它只有一种符合结合律的可逆运算，通常叫“乘法”。假设，这种运算也符合交换律，那么就叫阿贝尔群 (Abelian Group)。要是有两种运算，一种叫加法，满足交换律和结合律，一种叫乘法，满足结合律，它们之间满足分配律，这种丰富一点的结构叫做环 (Ring)，如果环上的乘法满足交换律，就叫可交换环 (Commutative Ring)。倘若，一个环的加法和乘法具有了所有的良好性质，那么就成为一个域 (Field)。基于域，我们允许建立一种新的结构，能进行加法和数乘，就构成了线性代数 (Linear algebra)。

代数的好处在于，它只关心运算规则的演绎，而不管参与运算的对象。只要定义恰当，完全可以让一只猫乘一只狗得到一头猪。基于抽象运算规则得到的所有定理完全可以运用于上面说的猫狗乘法。当然，在实际运用中，我们还是希望用它干点有意义的事情。学过抽象代数的都知道，基于几条最简单的规则，比如结合律，就能导出非常多的重要结论——这些结论可以应用到一切满足这些简单规则的地方——这是代数的威力所在，我们不再需要为每一个具体领域重新建立这么多的定理。

抽象代数有在一些基础定理的基础上，进一步的研究往往分为两个流派：研究有限的离散代数结构（比如有限群和有限域），这部分内容通常用于数论，编码，和整数方程这些地方；另外一个流派是研究连续的代数结构，通常和拓扑与分析联系在一起（比如拓扑群，李群）。我在学习中的 focus 重要是后者。

线性代数：“线性”的基础地位

对于做 Learning, vision, optimization 或者 statistics 的人来说，接触最多的莫过于线性代数——这也是我们在大学低年级就开始学习的。线性代数，包括建立在它基础上的各种学科，最核心的两个概念是向量空间和线性变换。线性变换在线性代数中的地位，和连续函数在分析中的地位，或者同态映射在群论中的地位是一样的——它是保持基础运算（加法和数乘）的映射。

在 learning 中有这样的一种倾向——鄙视线性算法，标榜非线性。也许在很多场合下面，我们应该非线性来描述麻烦的现实世界，但是无论什么时候，线性都是具有根本地位的。没有线性的基础，就不可能存在所谓的非线性推广。我们常用的非线性化的方法包括流形和 kernelization，这两者都需要在某个阶段回归线性。流形需要在每个局部建立和线性空间的映射，经过把许多局部线性空间连接起来形成非线性；而 kernelization 则是借助置换内积结构把原线性空间“非线性”地映射到另外一个线性空间，再进行线性空间中所能进行的操作。而在分析领域，线性的运算更是无处不在，微分，积分，傅立叶变换，拉普拉斯变换，还有统计中的均值，通通都是线性的。

泛函分析：从有限维向无限维迈进

泛函分析。就是在大学中学习的线性代数，它的简单主要因为它是在有限维空间进行的，因为有限，我们无须借助于太多的分析手段。然而，有限维空间并不能奏效地表达我们的世界——最重要的，函数构成了线性空间，可是它是无限维的。对函数进行的最主要的运算都在无限维空间进行，比如傅立叶变换和小波分析。这表明了，为了研究函数（或者说连续信号），我们需要打破有限维空间的束缚，走入无限维的函数空间——这里面的第一步，就

泛函分析 (Functional Analysis) 是研究的是一般的线性空间，包括有限维和无限维，但是很多东西在有限维下显得很 trivial，真正的困难往往在无限维的时候出现。在泛函分析中，空间中的元素还是叫向量，但是线性变换通常会叫作“算子”(operator)。除了加法和数乘，这里进一步加入了一些运算，比如加入范数去表达“向量的长度”或者“元素的距离”，这样的空间叫做“赋范线性空间”(normed space)，再进一步的，可以加入内积运算，这样的空间叫“内积空间”(Inner product space)。

大家发现，当进入无限维的时候，很多老的观念不再适用了，一切都需要重新审视。

1. 所有的有限维空间都是完备的（柯西序列收敛），很多无限维空间却是不完备的（比如闭区间上的连续函数）。在这里，完备的空间有特殊的名称：完备的赋范空间叫巴拿赫空间 (Banach space)，完备的内积空间叫希尔伯特空间 (Hilbert space)。
2. 完全同构的，而在无限维空间中，它们存在微妙的差别。就是在有限维空间中空间和它的对偶空间的
3. 给函数求导。就是在有限维空间中，所有线性变换（矩阵）都是有界变换，而在无限维，很多算子是无界的 (unbounded)，最重要的一个例子
4. 在有限维空间中，一切有界闭集都是紧的，比如单位球。而在所有的无限维空间中，单位球都不是紧的——也就是说，行在单位球内撒入无限个点，而不出现一个极限点。
5. 在有限维空间中，线性变换（矩阵）的谱相当于全部的特征值，在无限维空间中，算子的谱的结构比这个复杂得多，除了特征值组成的点谱 (point spectrum)，还有 approximate point spectrum 和 residual spectrum。纵然麻烦，可是，也更为有趣。由此形成了一个相当丰富的分支——算子谱论 (Spectrum theory)。
6. 在有限维空间中，任何一点对任何一个子空间总存在投影，而在无限维空间中，这就不一定了，具有这种良好特性的子空间有个专门的名称切比雪夫空间 (Chebyshev space)。该概念是现代逼近理论的基础 (approximation theory)。函数空间的逼近理论在 Learning 中应该有着相当重要的作用，但是现在看到的运用现代逼近理论的文章并不多。

继续往前：巴拿赫代数，调和分析，和李代数

基本的泛函分析继续往前走，有两个要紧的方向。第一个是巴拿赫代数 (Banach Algebra)，它就是在巴拿赫空间（完备的内积空间）的基础上引入乘法（这不同于数乘）。比如矩阵——它除了加法和数乘，还能做乘法——这就构成了一 个巴拿赫代数。除此以外，值域完备的有界算子，平方可积函数，都能构成巴拿赫代数。巴拿赫代数是泛函分析的抽象，很多对于有界算子导出的结论，还有算子谱论中的许多定理，它们不仅仅对算子适用，它们其实行从一般的巴拿赫代数中得到，并且应用在算子以外的地方。巴拿赫代数让你站在更高的高度看待泛函分析中的结论，但是，我对它在实际问题中能比泛函分析能多带来什么东西还有待思考。

最能把泛函分析和实际问题在一起的另一个重要方向是调和分析 (Harmonic Analysis)。我在这里列举它的两个子领域，傅立叶分析和小波分析，我想这已经能说明它的实际价值。它研究的最核心的问题就是怎么用基函数去逼近和构造一个函数。它研究的是函数空间的挑战，不可避免的必须以泛函分析为基础。除了傅立叶和小波，调和分析还研究一些很有用的函数空间，比如 Hardy space，Sobolev space，这些空间有很多很好的性质，在工程中和物理学中都有很重要的应用。对于 vision 来说，调和分析在信号的表达，图像的构造，都是十分有用的工具。

好的，继续之前的思路：

当分析和线性代数走在一起，产生了泛函分析和调和分析；当分析和群论走在一起，我们就有了李群 (Lie Group) 和李代数 (Lie Algebra)。它们给连续群上的元素赋予了代数结构。我一直认为这是一门非常漂亮的数学：在一个体系中，拓扑、微分和代数走到了一起。在一定条件下，通过李群和李代数的联系，它让几何变换的结合变成了线性运算，让子群化为线性子空间，这样就为 Learning 中许多要紧的模型和算法的引入到对几何运动的建模创造了必要的条件。因此，我们相信李群和李代数对于 vision 有着重要意义，只不过学习它的道路可能会很艰辛，在它之前应该学习很多别的数学。

现代概率论：在现代分析基础上再生

最后，再简单说说很多 Learning 的研究者特别关心的数学分支：概率论。自从 Kolmogorov 在上世纪 30 年代把测度引入概率论以来，测度理论就成为现代概率论的基础。在这里，概率定义为测度，随机变量定义为可测函数，条件随机变量定义为可测函数在某个函数空间的投影，均值则是可测函数对于概率测度的积分。值得注意的是，很多的现代观点，开始以泛函分析的思路看待概率论的基础概念，随机变量构成了一个向量空间，而带符号概率测度则构成了它的对偶空间，其中一方施加于对方就形成均值。角度即使不一样，不过这两种方式殊途同归，形成的基础是等价的。

在现代概率论的基础上，许多传统的分支得到了极大丰富，最有代表性的包括鞅论 (Martingale)——由研究赌博引发的理论，现在主要用于金融。这一点也反映出赌博和金融之间存在着深刻的理论联系。此外，布朗运动 (Brownian Motion) 是连续随机过程的基础，以及在此基础上建立的随机分析 (Stochastic Calculus)，包括随机积分（对随机过程的路径进行积分，其中比较有代表性的叫伊藤积分 (Ito Integral)），和随机微分方程。对于连续几何运用建立概率模型以及对分布的变换的研究离不开这些方面的知识。

---

篇外

12 Groundbreaking Mathematical Discoveries and Theories

12 项开创性的数学发现与理论

Mathematics has been a cornerstone of human advancement, unlocking mysteries of the universe and providing solutions to complex problems. Throughout history, mathematical discoveries and theories have propelled civilizations into new eras of knowledge and innovation. These breakthroughs have not only transformed scientific fields but have also reshaped our understanding of reality itself. In this article, we’ll explore 12 groundbreaking mathematical discoveries and theories that have left indelible marks on the world, sparking advancements across various disciplines and inspiring future generations of thinkers and dreamers.
数学一直是人类进步的基石，它揭开了宇宙的奥秘，为繁琐问题给出了解决方案。纵观历史，数学发现与理论推动人类文明进入了新的知识与创新时代。这些突破不仅改变了科学领域，还重塑了我们对现实本身的理解。在本文中，我们将探讨 12 项开创性的数学发现与理论，它们在世界上留下了不可磨灭的印记，推动了各个学科的进步，并激励着未来一代又一代的思想家与梦想家。

Pythagorean Theorem

毕达哥拉斯定理

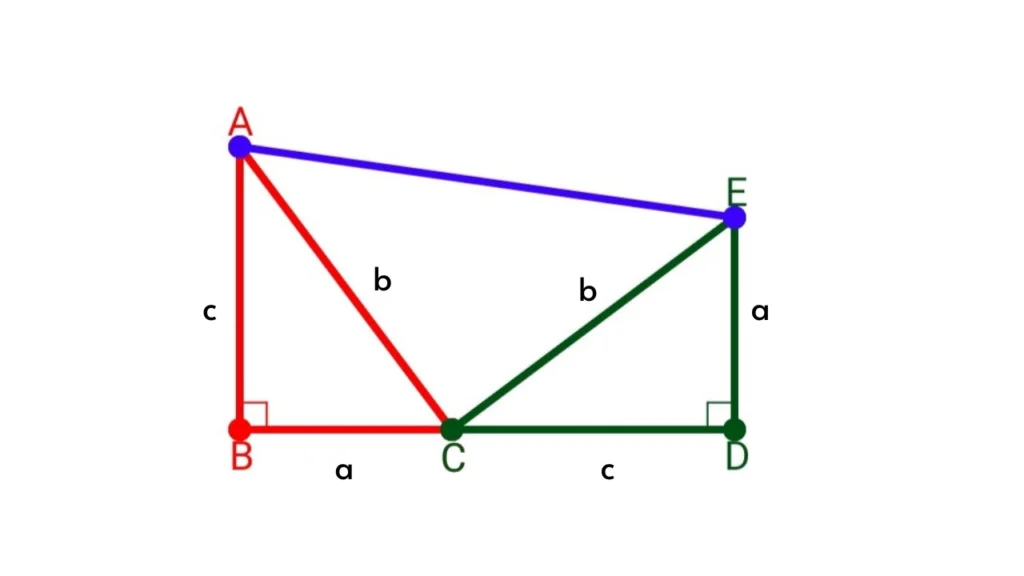
Proof of the Pythagorean Theorem. Image by Mohithasan61 via Openverse
毕达哥拉斯定理的证明。图片由 Mohithasan61 献出，来自 Openverse

One of the most well-known mathematical discoveries is the Pythagorean Theorem, a fundamental principle in geometry. Named after the ancient Greek mathematician Pythagoras, this theorem establishes the relationship between the sides of a right triangle. It states that the square of the hypotenuse’s length is equal to the sum of the squares of the other two sides’ lengths, i.e., ( c^2 = a^2 + b^2 ) (where ( c ) is the hypotenuse, and ( a ), ( b ) are the other two sides). This discovery has not only shaped the field of mathematics but has also been instrumental in architectural design, engineering projects, and various scientific fields, proving its timeless relevance.
几何学中的一项基本原理。该定理以古希腊数学家毕达哥拉斯的名字命名，确立了直角三角形三边之间的关系。其内容为：直角三角形斜边长度的平方等于另外两条直角边长度的平方和，即( c^2 = a^2 + b^2 )（其中( c )为斜边，( a )、( b )为另外两条边）。这一发现不仅塑造了数学领域，还在建筑设计、工程项目和各类科学领域中发挥了重要作用，彰显了其永恒的价值。就是最著名的数学发现之一是毕达哥拉斯定理，它

Calculus

微积分

Ada Lovelace calculus notes on paper. Image by Ada Lovelace Public domain via Wikimedia Commons
埃达·洛夫莱斯的微积分笔记手稿。图片由埃达·洛夫莱斯提供，属于公有领域，来自维基共享资源

In the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz independently developed calculus, a branch of mathematics that deals with continuous change. Calculus is divided into differential and integral calculus, focusing on the rates of change and accumulation, respectively. This groundbreaking discovery has been pivotal in physics, engineering, economics, and beyond, providing tools to model dynamic systems and describe the natural phenomena of the universe.
17 世纪，艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨各自独立创立了微积分——一门研究连续变化的数学分支。微积分分为微分学和积分学，分别侧重于变化率和累积量的研究。这一开创性发现在物理学、工程学、经济学等众多领域都至关重要，为建模动态系统和描述宇宙自然现象提供了工具。

Complex Numbers

复数

Complex numbers, a concept that extends the real numbers to include imaginary units, revolutionized mathematics and physics. The introduction of imaginary numbers, where the square root of -1 is denoted as ‘i’ (i.e., ( i = \sqrt{-1} )), allowed mathematicians to solve equations that previously seemed impossible. This breakthrough has applications in various fields such as electrical engineering, quantum mechanics, and applied mathematics, offering a richer understanding of numerical systems.
复数是将实数扩展到含有虚数单位的概念，它彻底改变了数学和物理学。虚数的引入（其中 -1 的平方根记为“i”，即( i = \sqrt{-1} )）使数学家能够解决此前看似无法解决的方程。这一突破在电气工程、量子力学和应用数学等多个领域都有应用，让我们对数字系统有了更深入的理解。

Non-Euclidean Geometry

非欧几里得几何

The development of non-Euclidean geometry challenged the long-standing assumptions of Euclidean geometry and introduced new perspectives on space. Mathematicians like Carl Friedrich Gauss, Nikolai Lobachevsky, and János Bolyai explored geometries where parallel lines can converge or diverge, providing the groundwork for Einstein’s theory of general relativity. This innovative framework transformed our understanding of the universe’s structure and continues to inspire mathematical research today.
非欧几里得几何的发展挑战了欧几里得几何长期以来的假设，并为空间研究引入了新视角。卡尔·弗里德里希·高斯、尼古拉·罗巴切夫斯基和亚诺什·波尔约等数学家探索了平行线允许相交或发散的几何体系，为爱因斯坦的广义相对论奠定了基础。这一创新性框架改变了我们对宇宙结构的理解，至今仍在激励着数学研究。

Number Theory

数论

Number theory, often referred to as the “Queen of Mathematics,” plays a crucial role in understanding the properties of integers. This field has attracted the curiosity of great mathematicians such as Pierre de Fermat and Carl Friedrich Gauss. From the enthralling mysteries of prime numbers to cryptographic applications in cybersecurity, number theory has had far-reaching implications, bridging abstract mathematical concepts with practical solutions to real-world problems.
数论常被称为“数学皇后”，在理解整数性质方面发挥着关键作用。这一领域吸引了皮埃尔·德·费马和卡尔·弗里德里希·高斯等伟大数学家的关注。从引人入胜的质数奥秘到网络安全中的密码学应用，数论的影响深远，它架起了抽象数学概念与现实问题实际解决方案之间的桥梁。

Game Theory

博弈论

Game theory, pioneered by John von Neumann and Oskar Morgenstern, offers a mathematical framework for analyzing competitive situations where the outcomes depend on the actions of multiple agents. This revolutionary approach has applications spanning economics, political science, psychology, and military strategy, where understanding strategic interactions can optimize decision-making processes in complex environments.
博弈论由约翰·冯·诺依曼和奥斯卡·摩根斯特恩开创，它提供了一个数学框架，用于分析结果取决于多个参与者行为的竞争情境。这种创新性技巧在经济学、政治学、心理学和军事战略等多个领域都有应用，通过理解策略互动，可优化复杂环境中的决策过程。

Chaos Theory

混沌理论

Chaos theory, which explores the behavior of dynamic systems highly sensitive to initial conditions, reshaped our understanding of seemingly random phenomena. Popularized by Edward Lorenz and the famous “butterfly effect,” chaos theory has applications in meteorology, astronomy, and population dynamics. It emphasizes the inherent unpredictability of complex systems and has provided valuable insights into natural and engineered systems.
混沌理论研究对初始条件高度敏感的动态系统行为，它重塑了我们对看似随机现象的理解。由爱德华·洛伦兹和著名的“蝴蝶效应”推广开来的混沌理论，在气象学、天文学和种群动力学等领域都有应用。它强调了复杂系统固有的不可预测性，并为自然系统和工程系统提供了宝贵的见解。

Fractals

分形

Fractals, popularized by mathematician Benoit Mandelbrot, are geometric objects characterized by self-similarity and intricate patterns at every scale. Fractals appear in nature, art, and computer graphics, offering beautiful visual representations of mathematical concepts. This discovery has impacted fields such as computer science, biology, and the visual arts, showcasing the profound interconnectedness between nature and mathematics.
一类具有自相似性的几何对象，在各种尺度下都呈现出复杂的图案。分形出现在自然界、艺术和计算机图形中，为数学概念供应了优美的视觉表现。这一发现对计算机科学、生物学和视觉艺术等领域产生了影响，展现了自然与数学之间深刻的内在联系。就是分形由数学家伯努瓦·曼德博推广开来，

Probability Theory

概率论

Some applied probability theory. Image by brewbooks via Openverse
一些应用概率论的内容。图片由 brewbooks 提供，来自 Openverse

Probability theory, which quantifies uncertainty and randomness, is foundational to statistics and many scientific fields. Developed by mathematicians like Blaise Pascal and Pierre-Simon Laplace, this theory provides tools to model uncertain events and analyze random processes. Its applications range from risk assessment and decision-making to physics and finance, highlighting its significance in managing and understanding the unpredictability of the world.
统计学和许多科学领域的基础。由布莱士·帕斯卡和皮埃尔-西蒙·拉普拉斯等数学家发展起来的这一理论，提供了建模不确定事件和分析随机过程的程序。它的应用范围从风险评估、决策制定到物理学和金融学，凸显了其在应对和理解世界不确定性方面的重要性。就是概率论对不确定性和随机性进行量化，

Set Theory

集合论

Equations and quantum theory. Image by geralt via Pixabay
方程与量子理论。图片由 geralt 提供，来自 Pixabay

Set theory, pioneered by Georg Cantor, introduced a new way to understand and organize mathematical collections. This theory forms the basis for modern mathematics, providing a unified framework to address the complexities of mathematical infinity and the structure of mathematical objects. Set theory’s influence extends to logic, computer science, and philosophy, where it continues to be a foundational element of mathematical thought.
数学思想的基础要素。就是集合论由格奥尔格·康托尔开创，它引入了一种理解和组织数学集合的新方法。这一理论是现代数学的基础，为处理数学无穷的复杂性和数学对象的结构提供了统一框架。集合论的影响延伸到逻辑学、计算机科学和哲学领域，至今仍

Topology

拓扑学

Topology, often described as “rubber-sheet geometry,” investigates the properties of space that are preserved under continuous transformations. This branch of mathematics has driven breakthroughs in understanding spatial relationships and connectivity. It has significant implications in fields such as robotics, data analysis, and cosmology, demonstrating its versatility in addressing both theoretical and practical challenges.
拓扑学常被描述为“橡皮膜几何”，它研究在连续变换下保持不变的空间性质。这一数学分支推动了对空间关系和连通性的突破性理解。它在机器人技巧、数据分析和宇宙学等领域具有重要意义，展现了其在应对理论和实际挑战方面的多功能性。

Algebraic Geometry

代数几何

Algebraic geometry, a discipline that explores geometrical structures through the lens of algebra, offers profound insights into the connections between algebraic equations and geometrical forms. This influential field has bridged the gap between abstract algebra and geometry, impacting number theory, string theory, and cryptography. The development of algebraic geometry has enabled mathematicians to delve into complex realms of mathematical theory and uncover new horizons of knowledge.
代数几何是一门通过代数视角探索几何结构的学科，它深刻揭示了代数方程与几何形式之间的联系。这一具有影响力的领域架起了抽象代数与几何学之间的桥梁，对数论、弦理论和密码学产生了影响。代数几何的发展使数学家能够深入探索复杂的数学理论领域，开拓新的知识视野。

Conclusion

结论

The journey through these 12 groundbreaking mathematical discoveries and theories highlights the transformative power of mathematics in shaping human understanding and progress. Each breakthrough has not only advanced its own field but has also interwoven with other disciplines, enhancing our comprehension of the world and inspiring future explorations. As mathematics continues to evolve, the potential for new discoveries remains boundless, driven by the timeless curiosity and ingenuity of humanity.
对这 12 项开创性数学发现与理论的探索，凸显了数学在塑造人类认知与进步方面的变革力量。每一项突破不仅推动了其自身领域的发展，还与其他学科相互交织，加深了我们对世界的理解，并激励着未来的探索。随着数学的不断发展，在人类永恒的好奇心和创造力的驱动下，新发现的潜力是无限的。

---

via：

• MIT 牛人解说数学体系_| P.Linux Laboratory - 5 月 18th, 2010（已沉寂）
  https://www.penglixun.com/study/science/mit_math_system.html

• 12 Groundbreaking Mathematical Discoveries and Theories - discoverwildscience
  https://discoverwildscience.com/12-groundbreaking-mathematical-discoveries-and-theories-2-271144/