深入解析：Java 堆（优先级队列）

文章目录

• 优先级队列
• 模拟实现优先级队列
• • 向下调整建堆
  • 向上调整建堆
  • 堆的删除
• priorityQueue
• • 构造方法
  • 大根堆和小根堆的向上调整比较方法
  • 扩容
• 面试题
• 堆排序

优先级队列

priorityqueue：底层是一颗完全二叉树

1. 小根堆：根比左右孩子都小
2. 大根堆：根比左右孩子都大
3. 用数组存储

模拟实现优先级队列

向下调整建堆

1. 向下调整算法的时间复杂度：O(N)
   建堆的算法

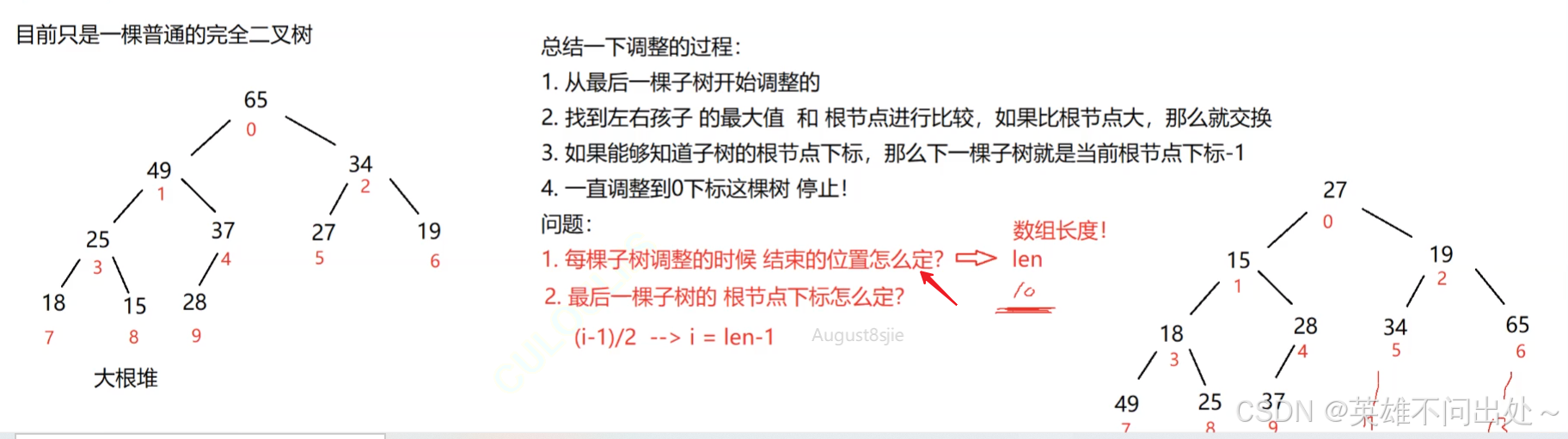
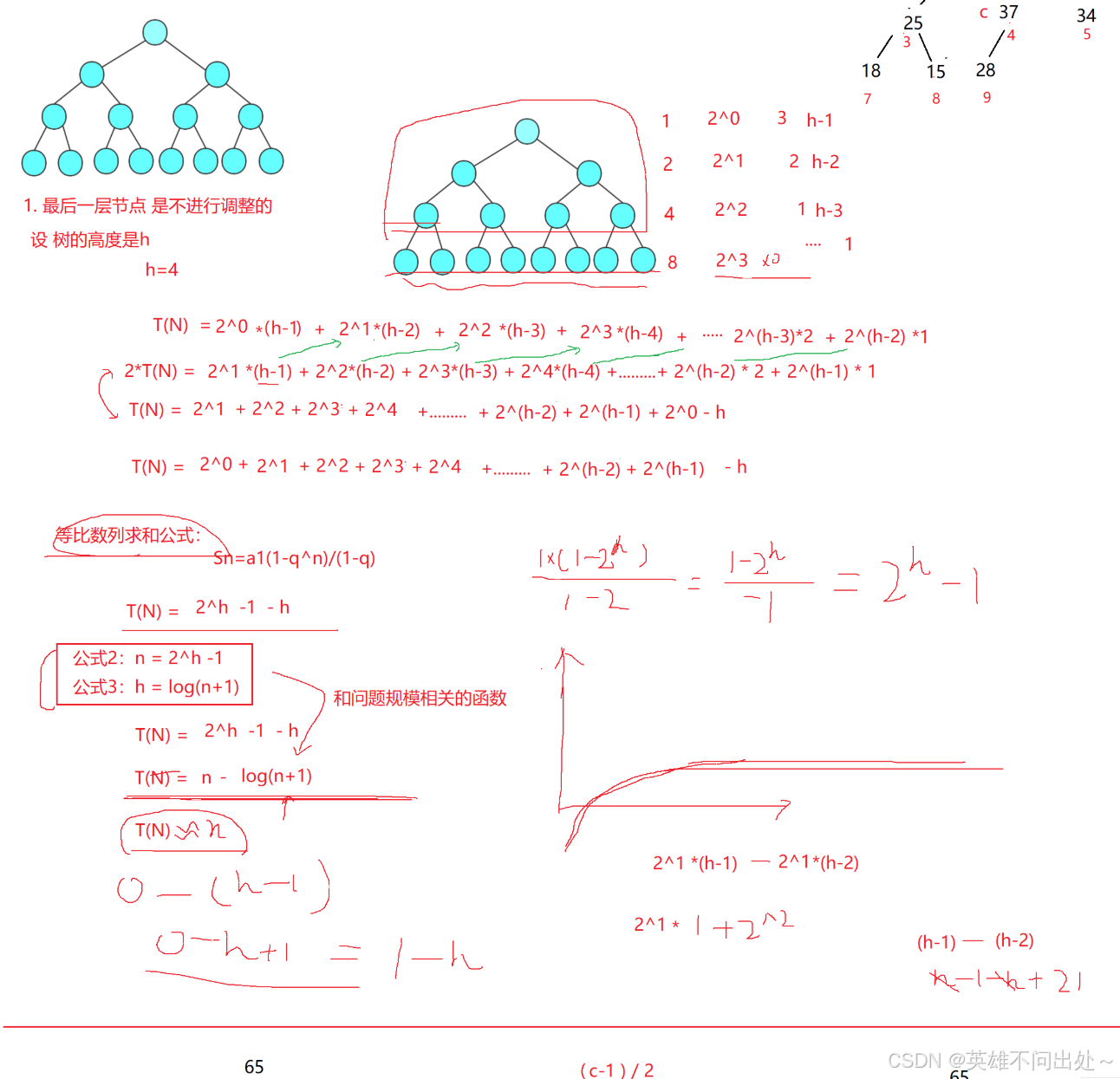
2. 推导过程：

// 向下调整算法
public void shifDown(int parent,int len){
// parent每次从根节点开始向下调整
// usedSize来检测是否还有得调,是否调结束了
int child = 2 * parent + 1;
// 至少有右孩子
while(child < len){
// 左右孩子比较大小,如果右孩子大,那么child+1
if(child + 1 < len && elem[child] < elem[child + 1]){
child = child + 1;
}
// if语句走完,证明child是左右孩子中大的那个的下标
if(elem[child] > elem[parent]){
int tmp = elem[child];
elem[child] = elem[parent];
elem[parent] = tmp;
parent = child;
child = parent * 2 + 1;
}else{
// 证明左右孩子中最大的那个都比父亲节点小,
// 是大根堆,不用调整了
break;
}
}
}

向上调整建堆

1. 新插入一个节点并且向上调整为大根堆
2. 向上调整建堆的时间复杂度是：O(N * logN)

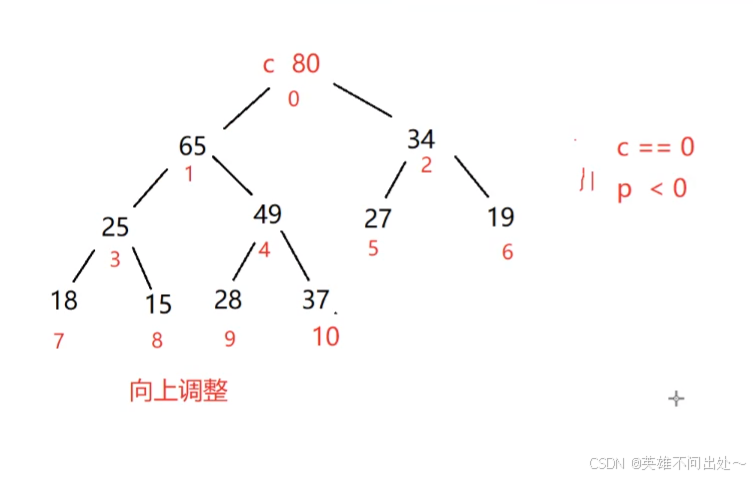
// 插入一个节点向上调整算法
public void push(int val){
// 满了,扩容
if(isFull()){
elem = Arrays.copyOf(elem,2 * elem.length);
}
elem[usedSize] = val;
// 向上调整,usedSize为新插入元素的下标
siftUp(usedSize);
usedSize++;
}
public void swap(int i,int j){
int tmp = elem[i];
elem[i] = elem[j];
elem[j] = tmp;
}
public boolean isFull(){
return usedSize == elem.length;
}
public void siftUp(int child){
// 通过孩子节点找到父亲节点下标
// 只要child大于0还需要调整,=0就不需要调整了
while(child >
0) {
int parent = (child - 1) / 2;
if (elem[parent] < elem[child]) {
swap(child, parent);
child = parent;
parent = (child - 1) / 2;
} else {
// parent下标对应的元素大于child下标对应的元素
// 不需要交换
break;
}
}
}

堆的删除

1. 让堆顶元素和最后一个元素交换
2. 然后让usedSize–，就删除了最后一个元素
3. 最后只需要调整0下标这棵树就行了，使用向下调整算法

public int pop(){
// 判空
if(empty()){
return -1;
}
int tmp = elem[0];
swap(0,usedSize - 1);
usedSize--;
shifDown(0,usedSize);
return tmp;
}
public boolean empty(){
return usedSize == 0;
}

priorityQueue

1. Java中的优先级队列默认是小根堆

public static void main(String[] args) {
// 默认是小根堆
PriorityQueue<
Integer> priorityQueue = new PriorityQueue<
>();
priorityQueue.offer(1);
priorityQueue.offer(5);
priorityQueue.offer(6);
System.out.println(priorityQueue.poll());
// 1
System.out.println(priorityQueue.poll());
// 5
}

2. PriorityQueue必须存放可以比较大小的元素
3. 不能插入null对象，否则会抛出空指针异常
4. 没有容量限制，可以插入任意多个元素，其内部可以自动扩容，在堆上开空间的
5. 插入和删除的时间复杂度都是O(logN)

构造方法

大根堆和小根堆的向上调整比较方法

1. 插入元素，向上调整，向上调整的比较方法
   
   
   

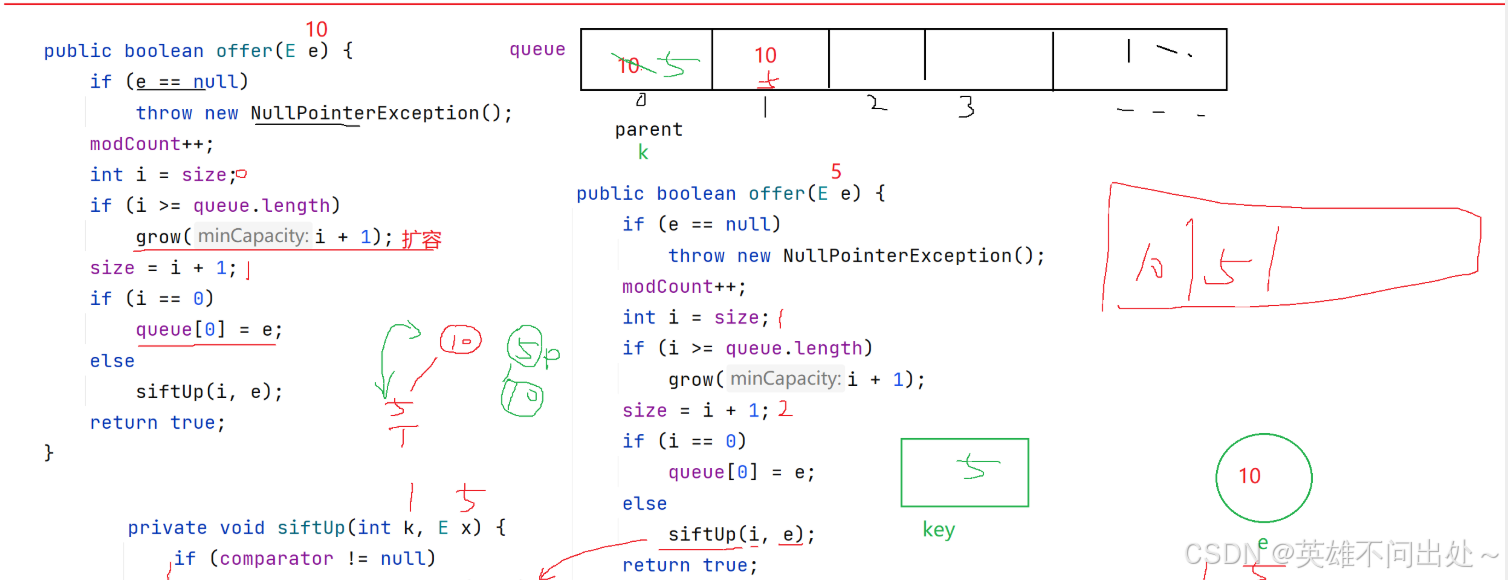
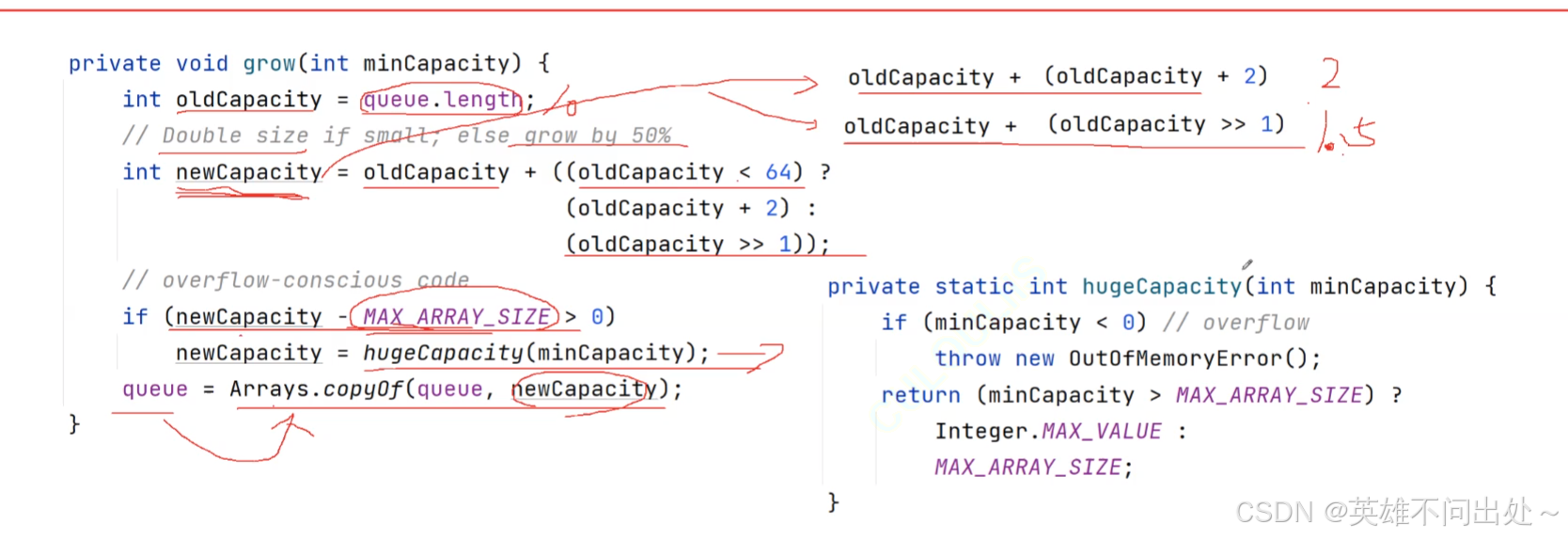
扩容

1. 要么2倍扩容，要么1.5倍扩容
   

面试题

1. top-k问题：
   解法一：
   比如得到最小的前k个元素
   建立一个小根堆
   出k次元素得到最小的前k个元素

解法二：
求最小的前k个元素，先把前k个元素建立大根堆，再和k+1位置的元素比较，如果小于堆顶元素就入堆，并且删除堆顶元素，以此类推，最后剩下的k个元素就是最小的元素

3. top-k问题的时间复杂度是：O(N * logK)
求最小的K个数

// class Imp implements Comparator<Integer> {
  // public int compare(Integer o1,Integer o2){
  // return o2.compareTo(o1);
  // }
  // }
  class Solution
  {
  public int[] smallestK(int[] arr, int k) {
  int[] ret = new int[k];
  if(arr == null || k <= 0){
  return ret;
  }
  // new一个比较器,匿名内部类的方法
  PriorityQueue<
  Integer> priorityQueue = new PriorityQueue<
  >(new Comparator<
  Integer>(){
  public int compare(Integer o1,Integer o2){
  return o2.compareTo(o1);
  }
  });
  // 建立k个元素的大根堆
  // K * logK
  for(int i = 0;i < k;i++){
  priorityQueue.offer(arr[i]);
  }
  // O((N-k) * logK)
  for(int i = k;i < arr.length;i++){
  int top = priorityQueue.peek();
  if(top > arr[i]){
  priorityQueue.poll();
  priorityQueue.offer(arr[i]);
  }
  }
  // 总的时间复杂度: O(N * logK)
  // K * logK
  // 整理元素不算入top-k问题中
  for(int i = 0;i < k;i++){
  ret[i] = priorityQueue.poll();
  }
  return ret;
  }
  }

堆排序

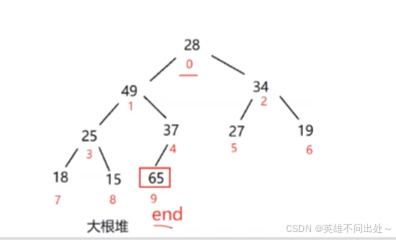
1. 从大到小或者是从小到大排序
2. 从小到大排序，建立大根堆，每次最后一个元素和堆顶元素交换，usedSize–，向下调整为大根堆，以此类推
3. 堆排序的时间复杂度：O(N * logN)

// 堆排序
public void heapSort(){
int end = usedSize - 1;
while(end >
0){
swap(0,end);
shifDown(0,end);
end--;
}
}
public static void main(String[] args) {
TestHeap testHeap = new TestHeap();
int array[] = {
27,15,19,18,28,34,65,49,25,37
};
testHeap.initElem(array);
// 向下调整建堆:O(N)
testHeap.createHeap();
System.out.println("======");
// O(N * logN)
testHeap.heapSort();
System.out.println("======");
}