机器学习之线性回归

在学习机器学习的基础之前，我们首先要认识几个必知的概念。E,P,T

就像做一件事之前我们都需要知道我们在干什么，怎么做的，EPT就是一条直白的线索。

首先是E（experience经验）：通俗的理解就是数据，就和升级就需要刷怪一样

之后是P（pcperformance性能/度量）：我们需要一些工具来评判你所做的好坏，实际上就是模型或者公式

最后就是T（task任务）：也就是我们的目的，它需要被性能所调节

 

首先我们最先接触到的就是数据，也就是特征和结果，因为这次的主题是线性回归，所以我们得到的结果必定是离散的。

这里我们写出特征的样本 X = [[1,x1,x2......]

　　　　　　　　　　　　　[1,x1,x2......]

　　　　　　　　　　　　　[1,x1,x2......]

　　　　　　　　　　　　　. . . . . .         ]

通常特征的表示有两种方式，横向和纵向，我们使用纵向，这里最大的疑惑在于每一个特征前都会有数字1，它的实际意义就是线性方程中y=kx+b中的b

常数是单独的个体，也是特征之一。

 

而Y = [ [y1],

　　　[y2],

　　    .......]

 

我们由简化繁，选取栗子的特征为2也就是X.shape[1] = 2

也就是

 X = [[1,x1]

　　[1,x1]

　　[1,x1]

　　. . . . . .]

就如同在y=kx+b中要想获得y，我们就必须获得k和b一样，我们设置一个未知数theta

theta = [theta1

　　　theta2]

这里的theta1代表常数b，theta2代表k

当我们使用矩阵相乘的原理，让X乘以theta

得到的是你的推测值也就是h

Y=[[theta1+theta2*x1],

　[theta1+theta2*x1],

　[theta1+theta2*x1]

        ......]

 

那么我们的Y是否准确呢？我们的性能度量P就出现了

这里的性能类似于方差，使用的是最小二乘法，得到的越小就表示越准确

p公式：

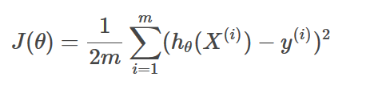
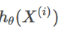 代表的就是预测的Y

显而易见的，代价函数J是一个二次函数，最低点就是最优值

之后我们会对J（theta）进行求theta的偏导，这得于一个结论，就是对任意的一个二次函数求导后，带入X，得到的结果正负会代表方向

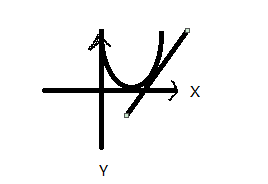当最优点在所选X点的左边，此时的斜率为正，用theta-deltatheta（theta偏导），结果接近最优点

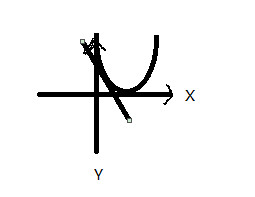同理，当最优点在所选X点的右边，此时的斜率为负，用theta-deltatheta（theta偏导），结果接近最优点

 

如果我们将这种操作做到一定次数，我们就会找到一个相对最优的结果，这个过程就是梯度下降

所以说，梯度下降是一种求函数最小值的算法，通过寻求使代价下降最大的参数组合

 

这里有一个偏导过程：

 

 

 

使theta = theta - α * deltatheta

α代表学习率，用来控制弧度，以防下降过度出现梯度震荡的情况

这里需要注意的是α需要不断调整的，之后我们可以通过网格搜索快速完成筛选

  

 python代码实现（需自定义参数）：

 

---------------------------------------------------------------------------------------------------------------------------------------------------

import numpy as np
from numpy import *

 

#定义代价函数costFunction
def costFunction(X,y,theta):
　　m=X.shape[0] #样本个数m
　　h=np.dot(X,theta) #计算预测值h
　　J=1.0/(2*m)*np.dot((h-y).T,(h-y)) #计算代价函数值
　　return J

#定义梯度下降算法函数
def gradDec(X,y,theta=0,alpha=0.005,iter_num=15000):
　　m,n=X.shape #样本个数m,列数n
　　theta=np.zeros((n,1)) #初始化theta值
　　J_history=np.zeros(iter_num) #初始化代价历史值

#开始梯度下降算法
for i in range(iter_num):
　　J_history[i]=costFunction(X,y,theta) #计算代价函数值
　　h=np.dot(X,theta) #计算预测值
　　deltatheta=1.0/m*np.dot(X.T,(h-y)) #计算deltatheta
　　theta-=alpha*deltatheta #更新theta

　　return J_history,theta

#执行梯度下降算法
J_history,theta=gradDec(X,y,iter_num=30000)

 

 

---------------------------------------------------------------------------------------------------------------------------------------------------