牛客小白月赛64
https://ac.nowcoder.com/acm/contest/49244
小杜要迟到了!
分析:
比较(n-1)a和 (n+k-2)b的大小,按要求输出结果即可。 时间复杂度O(1)
#include<bits/stdc++.h>
#define ll long long
#define L(i,j,k) for(ll i=(j);i<=(k);++i)
#define R(i,j,k) for(ll i=(j);i>=(k);--i)
#define inf 2e9
#define fi first
#define se second
#define pb push_back
#define mkp make_pair
#define MS(i,j) memset(i,j,sizeof (i))
const int N=1e6+10,M=10;
const int mod=998244353,mmod=mod-1;
const double pi=acos(-1),eps=1e-8;
using namespace std;
int m,n,t,x,y,z,l,r,u,v,k,p,pp,nx,ny,nz,ansx,ansy,mn,mx;
int a,b;
int rt,op,lim,pos,key,block;
int cnt,tot,num,sum,ans;
void solve(){
scanf("%d%d%d%d",&n,&k,&a,&b);
ll x=1ll*(n-1)*a;
ll y=1ll*(n+k-2)*b;
if(x>y)puts("1");
else if(x<y)puts("2");
else puts("0");
}
int main(){
int Case=1;
//scanf("%d",&Case);
while(Case--)solve();
}
小杜捕鱼
分析:
考虑哪个位置距离所有鱼的位置的最大值最大,即矩形鱼塘的四个角落。
分别计算撒网中心落在(1,1),(1,m),(n,1),(n,m)时,与所有鱼的曼哈顿距离的最大值。
四种结果再取一个最大值。 时间复杂度O(nm)
#include<bits/stdc++.h>
#define ll long long
#define L(i,j,k) for(int i=(j);i<=(k);++i)
#define R(i,j,k) for(int i=(j);i>=(k);--i)
#define inf 2e9
#define fi first
#define se second
#define pb push_back
#define mkp make_pair
#define MS(i,j) memset(i,j,sizeof (i))
const int N=1e3+10,M=10;
const int mod=998244353,mmod=mod-1;
const double pi=acos(-1),eps=1e-8;
using namespace std;
int m,n,t,x,y,z,l,r,u,v,k,p,pp,nx,ny,nz,ansx,ansy,mn,mx;
int a,b;
int rt,op,lim,pos,key,block;
int cnt,tot,num,sum,ans;
char s[N][N];
void solve(){
scanf("%d%d",&n,&m);
ans=0;
L(i,1,n)scanf("%s",s[i]+1);
L(i,1,n)L(j,1,m)if(s[i][j]=='#'){
ans=max(ans,i-1+j-1);
ans=max(ans,i-1+m-j);
ans=max(ans,n-i+j-1);
ans=max(ans,n-i+m-j);
}
printf("%d\n",ans);
}
int main(){
int Case=1;
//scanf("%d",&Case);
while(Case--)solve();
}
Karashi的生日蛋糕

分析:
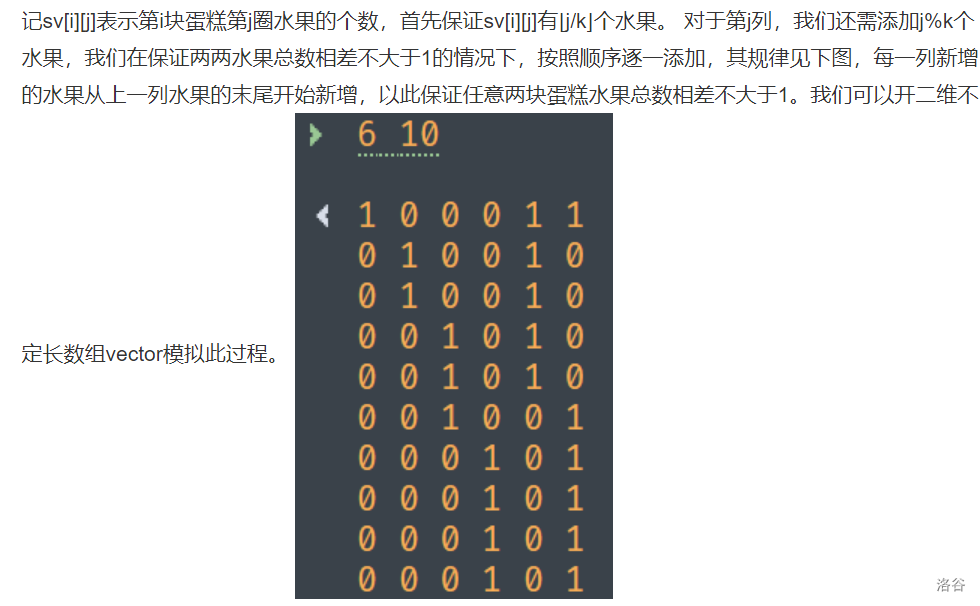
#include<bits/stdc++.h>
#define ll long long
#define L(i,j,k) for(int i=(j);i<=(k);++i)
#define R(i,j,k) for(int i=(j);i>=(k);--i)
#define inf 2e9
#define fi first
#define se second
#define pb push_back
#define mkp make_pair
#define MS(i,j) memset(i,j,sizeof (i))
const int N=1e3+10,M=10;
const int mod=998244353,mmod=mod-1;
const double pi=acos(-1),eps=1e-8;
using namespace std;
int m,n,t,x,y,z,l,r,u,v,k,p,pp,nx,ny,nz,ansx,ansy,mn,mx;
int rt,op,lim,pos,key,block;
int cnt,tot,num,sum,ans;
void solve(){
scanf("%d%d",&n,&k);
vector<vector<int> >sv(k+2,vector<int>(n+2,0));
p=1;
L(j,1,n)L(i,1,j%k){
sv[p][j]=1;
p++;
if(p>k)p-=k;
}
L(i,1,k){
L(j,1,n){
printf("%d ",sv[i][j]+j/k);
}
printf("\n");
}
}
int main(){
int Case=1;
//scanf("%d",&Case);
while(Case--)solve();
}
Karashi的树 I
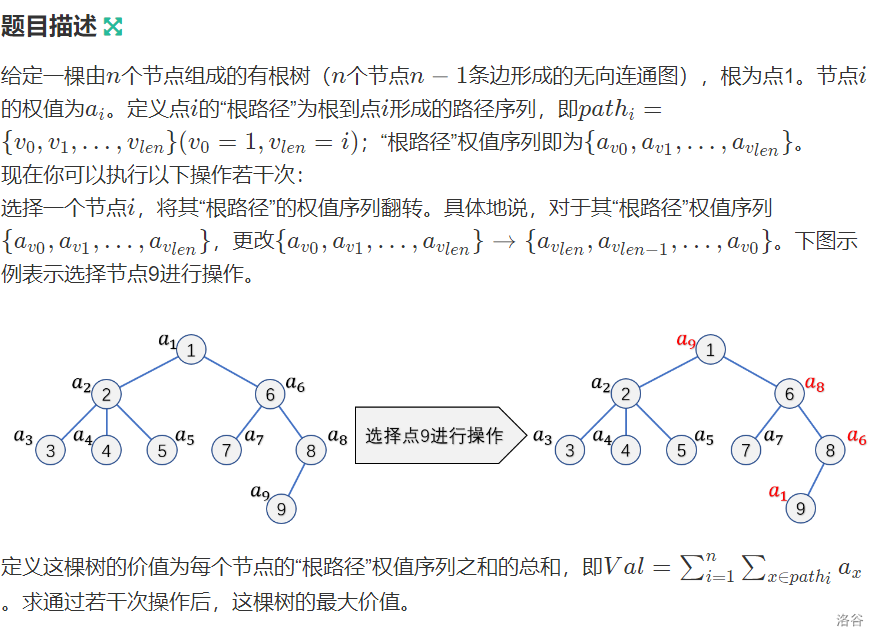
分析:
先考虑叶子节点上的值一定是最小的 我们一定能进行两次交换使得最小值先到根节点 再到叶子结点
同理处理完所有叶子结点 就产生新一层的叶子节点 所以我们一定能通过交换操作使得满足最大
考虑每个点对答案的贡献 为sz[u]×a[u] 其中sz[u]为u子树的大小
我们对所有的a排序 sz排序 相应地相乘即可满足最大
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=3e5+5;
int n;
ll a[maxn],num[maxn],ans;
vector<int>Q[maxn];
void solve();
void dfs(int);
int main(){
int T;T=1;
while(T--)solve();
return 0;
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
for(int i=2,x;i<=n;i++)scanf("%d",&x),Q[x].push_back(i);
dfs(1);
sort(a+1,a+1+n);
sort(num+1,num+1+n);
for(int i=1;i<=n;i++)
ans+=a[i]*num[i];
cout<<ans;
}
void dfs(int u){
num[u]=1;
for(int i=0;i<Q[u].size();i++){
int to=Q[u][i];
dfs(to);
num[u]+=num[to];
}
}
Karashi的数组

分析:

#include<bits/stdc++.h>
#define ll long long
#define L(i,j,k) for(int i=(j);i<=(k);++i)
#define R(i,j,k) for(int i=(j);i>=(k);--i)
#define inf 2e9
#define fi first
#define se second
#define pb push_back
#define mkp make_pair
#define MS(i,j) memset(i,j,sizeof (i))
const int N=1e6+10,M=10;
const int mod=998244353,mmod=mod-1;
const double pi=acos(-1),eps=1e-8;
using namespace std;
int m,n,t,x,y,z,l,r,u,v,k,p,q,pp,nx,ny,nz,ansx,ansy,mn,mx;
int rt,op,lim,pos,key,block;
int cnt,tot,len,num,sum,ans;
int a[N];
void solve(){
scanf("%d%d%d",&n,&m,&len);
L(i,1,n)scanf("%d",&a[i]);
ans=0;
L(k,1,n-len-1){
if(a[k]==0||a[k+len+1]==0)ans++;
}
while(m--){
scanf("%d%d",&pos,&x);
l=pos-len-1,r=pos;
if(1<=l&&l<=n-len-1&&a[l]!=0){
if(a[pos]==0)ans--;
if(x==0)ans++;
}
if(1<=r&&r<=n-len-1&&a[r+len+1]!=0){
if(a[pos]==0)ans--;
if(x==0)ans++;
}
printf("%d\n",ans);
a[pos]=x;
}
}
int main(){
int Case=1;
//scanf("%d",&Case);
while(Case--)solve();
}
小杜跑酷
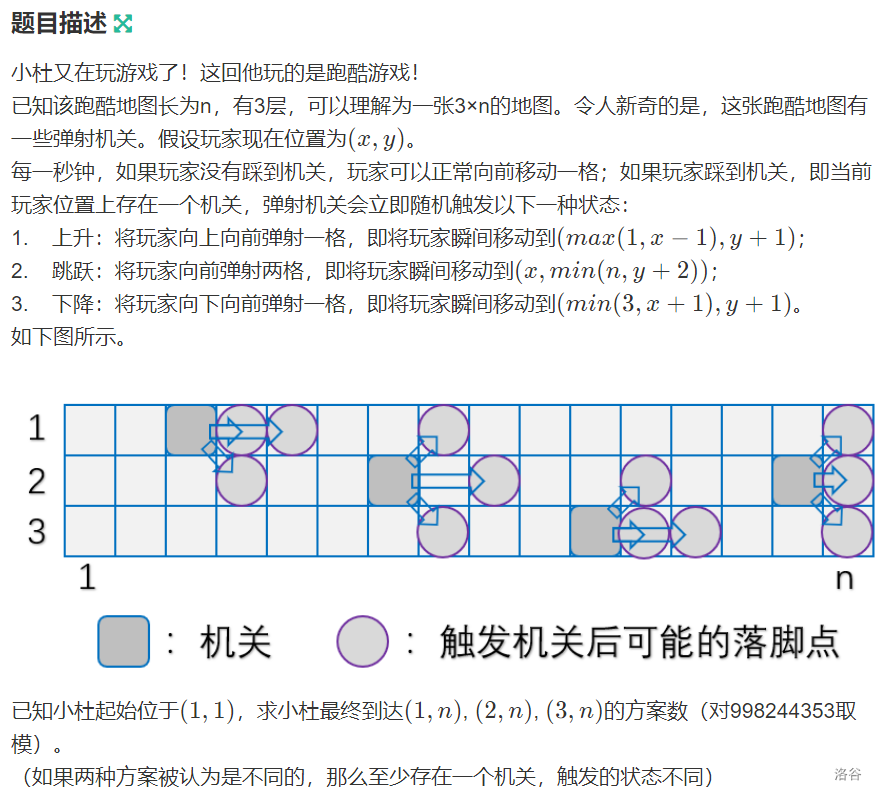
分析:
考虑到n有1e9 我们只用考虑机关 首先对每个机关所占的位置进行离散化
离散化之后就顺序转移即可
考虑位置<i,j> 如果<i,j-1>为非机关 dp[i][j]+=dp[i][j-1] 如果为机关 就按照题意相应转移即可
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int mod=998244353;
const int maxn=3e6+5;
void solve();
int n,m,cnt,len;
int b[maxn],vis[3][maxn];
ll dp[3][maxn];
struct node{
int x,y;
}a[maxn];
int find(int yy){
return lower_bound(b+1,b+1+len,yy)-b;
}
int main(){
int T;T=1;
while(T--)solve();
return 0;
}
void solve(){
cin>>n>>m;
for(int i=1;i<=m;i++)
scanf("%d%d",&a[i].x,&a[i].y),b[++cnt]=a[i].y,b[++cnt]=a[i].y+1,b[++cnt]=min(n,a[i].y+2),a[i].x--;
sort(b+1,b+1+cnt);
len=unique(b+1,b+1+cnt)-b-1;
for(int i=1;i<=m;i++)
a[i].y=find(a[i].y),vis[a[i].x][a[i].y]=1;
dp[0][1]=1;
for(int j=1;j<=len;j++){
for(int i=0;i<=2;i++){
if(!vis[i][j-1])
dp[i][j]=(dp[i][j]+dp[i][j-1])%mod;
if(vis[i][j]){
dp[max(0,i-1)][j+1]=(dp[i][j]+dp[max(0,i-1)][j+1])%mod;
dp[i][min(len,j+2)]=(dp[i][j]+dp[i][min(len,j+2)])%mod;
dp[min(2,i+1)][j+1]=(dp[i][j]+dp[min(2,i+1)][j+1])%mod;
}
}
}
cout<<dp[0][len]<<endl<<dp[1][len]<<endl<<dp[2][len];
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号