牛客挑战赛64

https://ac.nowcoder.com/acm/contest/42819

题目出得很好

分析：

很清晰的一道启发式合并 小集合合并到大集合

当 1 在大集合时 遍历小集合的时候就可统计答案

当 1 在小集合时 因为每个点最多只会统计一次答案 此时遍历大集合也能统计答案

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
#define int ll
const int maxn=2e5+5;
void solve();
int x,y,n,m1,m2,cnt;
int fa[maxn],ans[maxn];
vector<int>Q[maxn];
int find(int xx){
	if(fa[xx]!=xx)return fa[xx]=find(fa[xx]);
	return xx;
}
void add(int xx,int yy){
	int fx=find(xx),fy=find(yy),f1=find(1);
	if(fx==fy)return;
	if(Q[fx].size()<Q[fy].size())swap(fx,fy);
	if(f1==fy)
	for(int i=0;i<Q[fx].size();i++)
	ans[Q[fx][i]]=cnt;
	for(int i=0;i<Q[fy].size();i++){
		int to=Q[fy][i];
		Q[fx].push_back(to);
		if(fx==f1)ans[to]=cnt;
	}
	fa[fy]=fx;
	Q[fy].clear();
}
signed main(){
	int T;T=1;
	while(T--)solve();
     return 0;
}
void solve(){
	memset(ans,-1,sizeof(ans));
	ans[1]=0;
	cin>>n>>m1>>m2;
	for(int i=1;i<=n;i++)fa[i]=i,Q[i].push_back(i);
	for(int i=1;i<=m1;i++)cin>>x>>y,add(x,y);
	for(int i=1;i<=m2;i++)cin>>x>>y,cnt++,add(x,y); 
	for(int i=1;i<=n;i++)cout<<ans[i]<<endl;
}

分析：

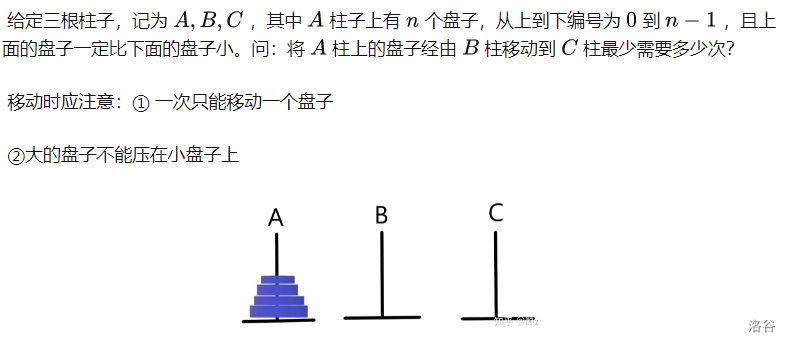
汉诺塔问题的变种

先来看标准的汉诺塔问题

递归写法：

def move(n,A,B,C)://n个盘子放在A 经过B 放在C上
    if n==1:             # 1个盘子，直接打印出移动动作
        print(A,'--->',C)
    else:                # n > 1时，用抽象出的3步来移动
        move(n-1, A, C, B) #step1.  把除了最大的盘子之外的盘子从A移到B
        print(A,'--->',C) #step2.  把最大的盘子从A移到C
        move(n-1, B, A, C) #step3.  把除了最大的盘子之外的盘子从B移到C

打表时候就会发现 1 3 5 7 15

发现f[i]=f[i-1]×2+1

怎么理解这个式子

回到本题来

60的数据肯定和标准的汉诺塔一样 能够推出一个式子 20的数据递归输出方案

推来推去发现推不出式子来 然后写递归 发现也不会 我太菜了唉

递归：

根据汉诺塔的常规套路，将除了最大盘之外的盘子堆到除 最大盘所在柱 的另一个非目标柱上，然后将最大盘移动到目标柱上，不断递归下去即可

具体地说，假设当前需要将 i号盘从 s移动到 t柱，那么我们将 [1,i)号盘全部堆到除 s,t外的那个柱子上，然后再将 i号盘堆到 t上即可。

#include <bits/stdc++.h>

using namespace std;

int n, b[65];

void dfs(int k, int t) {
    if (b[k] == t) return ;
    for (int i = k - 1; i; i--) dfs(i, 3 - b[k] - t);
    b[k] = t, printf("%d %c\n", k, t + 'A');
}

int main() {
    scanf("%d", &n);
    for (int i = 2; i <= n; i += 2) b[i] = 2;
    for (int i = n; i; i--) dfs(i, 1);
    return 0;
}

C Rolling Girl

#include <bits/stdc++.h>
#define remake return 0
using namespace std;
using ll = long long;

unsigned seed, mod;

unsigned read() {
    seed ^= seed << 13;
    seed ^= seed >> 5;
    seed ^= seed << 7;
    return seed % mod + 1;
}

const int N = 1e7 + 1, p = 1004535809;

ll a[N], g[N], f[N];

int main() {
    cin.tie(nullptr)->sync_with_stdio(false);
    int n;
    cin >> n >> seed >> mod;
    for (int i = 1; i <= n; i++) a[i] = read();
    memset(f, 63, sizeof(f));
    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        if (n % i == 0) {
            for (int j = i; j <= n; j += i) {
                g[j] = i;
                f[i] = min(f[i], a[j]);
            }
        }
        ans += ((n / g[i]) * f[g[i]]) % p;
        ans %= p;
    }
    cout << ans << '\n';
    remake;
}

D AND Sequence

#include<bits/stdc++.h>
#define ll long long
#define ls u<<1
#define rs u<<1|1
#define mm(x) memset(x,0,sizeof(x))
using namespace std;
int read()
{
	int a=0;int f=0;char p=getchar();
	while(!isdigit(p)){f|=p=='-';p=getchar();}
	while(isdigit(p)){a=(a<<3)+(a<<1)+(p^48);p=getchar();}
	return f?-a:a;
}
const int INF=998244353;
const int P=998244353;
const int N=1e6+5;
int T;
int n,m;
int val[N];
int ans;
int a[N],b[N];
int ma[N],mb[N];
int ta[N],topa;
int tb[N],topb;
vector<int >va[100],vb[100];
int x[N],y[N];
int topx,topy;
int tot[N];
void calc(int f)
{
	int res=0;
	tot[topy+1]=0;
	for(int k=topy;k>=1;--k)	tot[k]=(tot[k+1]+y[k]%P)%P;
	for(int p=1,q=0;p<=topx;++p)
	{
		while(q+1<=topy&&y[q+1]<=x[p])	q++;
		res=(res+(ll)x[p]*q%P)%P;
		res=(res+tot[q+1])%P;
	}
	if(f==-1)	res=(P-res)%P;
	ans=(ans+res)%P;
}
void solve(int l,int r)
{
	if(l==r)	return ;
	int mid=(l+r)>>1;
	solve(l,mid);	solve(mid+1,r);
	a[mid]=ma[mid]=val[mid];	b[mid+1]=mb[mid+1]=val[mid+1];
	for(int i=mid-1;i>=l;--i)	a[i]=a[i+1]&val[i],ma[i]=max(ma[i+1],val[i]);
	for(int i=mid+2;i<=r;++i)	b[i]=b[i-1]&val[i],mb[i]=max(mb[i-1],val[i]);
	
	topa=0;	ta[0]=-1;
	for(int i=mid;i>=l;--i)
	{
		if(a[i]!=ta[topa])
		{
			++topa;
			ta[topa]=a[i];
			va[topa].clear();
		}
		va[topa].push_back(i);
	}

	topb=0;	tb[0]=-1;
	for(int i=mid+1;i<=r;++i)
	{
		if(b[i]!=tb[topb])
		{
			++topb;
			tb[topb]=b[i];
			vb[topb].clear();
		}
		vb[topb].push_back(i);
	}
	int tmpx=ans;
	topx=0;	topy=0;
	for(int i=mid;i>=l;--i)	x[++topx]=ma[i];
	for(int i=mid+1;i<=r;++i)	y[++topy]=mb[i];
	calc(1);
	int tmpy=ans;
	for(int i=1;i<=topa;++i)
		for(int j=1;j<=topb;++j)
		{
			int sum=ta[i]&tb[j];
			topx=0;	topy=0;
			for(auto v:va[i])	if(val[v]!=sum)	x[++topx]=ma[v];
			for(auto v:vb[j])	if(val[v]!=sum)	y[++topy]=mb[v];
			calc(-1);
		}
}
int main()
{
	n=read();
	for(int i=1;i<=n;++i)	val[i]=read();

	solve(1,n);
	
	printf("%d\n",ans);
	return 0;
}