思维

https://codeforces.com/gym/102059/problem/G

题意：

一条街上一共 N 个点，需要在某些点上建路灯，使得整条街被照亮，一个路灯可以照亮左右两个点，每个点都有一个建路灯的花费。

现在你还有 K次机会，可以交换两个路灯的建造费用，求使得整条街被照亮的最小花费。( 1 ≤ N ≤ 250000 , 0 ≤ k ≤ 9 )

分析：

如果这道题没有 K 次交换路灯花费的操作的话，问题将会变得简单很多，只需要记录每个点某尾和前一个点的状态即可递推求解。

发现如果两灯交换位置 一定是一个亮一个不亮 如果两个灯都是亮的 就没必要进行交换的操作

因此如果当前位置需要亮 但是我们不要当前的灯亮 我们就先欠着 等着后面亮的灯与之交换即可

同理如果当前位置不需要亮 我们可以交换前面我们欠着的灯还上

当然也可以先还再欠

于是设计dp[i][j][o][0\1\2\3] 最后一维用二进制表示最后两个位置的亮灭状态 前i个位置 欠了j个 还了o个

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
#define int ll
const int maxn=250005;
int dp[maxn][10][10][4],a[maxn]; // 0-00 1-01 2-10 3-11
int n,k;
void solve();
signed main(){
	int T;T=1;
	while(T--)solve();
     return 0;
}
void solve(){
	cin>>n>>k;
	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
	memset(dp,0x3f,sizeof(dp));
	dp[0][0][0][2]=0;//欠了j个 还了o个 
	for(int i=1;i<=n;i++)
		for(int j=0;j<=k;j++)
			for(int o=0;o<=k;o++){
				dp[i][j][o][0]=dp[i-1][j][o][2];
				dp[i][j][o][1]=min(dp[i-1][j][o][0],dp[i-1][j][o][2])+a[i];
				dp[i][j][o][2]=min(dp[i-1][j][o][1],dp[i-1][j][o][3]);
				dp[i][j][o][3]=min(dp[i-1][j][o][1],dp[i-1][j][o][3])+a[i];
				if(j>0){
					dp[i][j][o][1]=min(dp[i][j][o][1],min(dp[i-1][j-1][o][0],dp[i-1][j-1][o][2]));
					dp[i][j][o][3]=min(dp[i][j][o][3],min(dp[i-1][j-1][o][1],dp[i-1][j-1][o][3]));
				}
				if(o>0){
					dp[i][j][o][0]=min(dp[i][j][o][0],dp[i-1][j][o-1][2]+a[i]);
					dp[i][j][o][2]=min(dp[i][j][o][2],min(dp[i-1][j][o-1][1],dp[i-1][j][o-1][3])+a[i]);
				}
			
	}
	ll ans=1e17; 
	for(int i=0;i<=k;i++)
	ans=min(min(ans,dp[n][i][i][1]),min(dp[n][i][i][2],dp[n][i][i][3]));
	cout<<ans;
}

分析：

乍一看 非常像当年noip搭积木 只不过这个是从外围不断往里删

思路还是一样的 dp[i]表示前i个全部删完的操作数

考虑当前位置i的积木 有两种情况

（1）dp[i-1]+1 前面i-1个已经删完 现在只需要多一步操作即可消灭i位置

（2）h[i] 表示需要当前位置一个一个从上往下删除 （这种情况的前提是h[i-1]≥h[i]≤h[i+1]，如果h[i]>h[i+1]（h[i-1]），i位置的最优策略一定不是h[i]）

对两种情况取个min

同理从右边再转移一次 最后统计每个位置需要的最大操作数即可

void slove() {
	cin >> n;
	for (int i = 1; i <= n; i++)cin >> h[i];
	for (int i = 1; i <= n; i++)dp1[i] = min(dp1[i - 1] + 1, h[i]);
	for (int i = n; i >= 1; i--)dp2[i] = min(dp2[i + 1] + 1, h[i]);
	int ans = 0;
	for (int i = 1; i <= n; i++)ans = max(ans, min(dp1[i], dp2[i]));
	cout << ans << endl;
}

Codeforces Round #621 E. Cow and Treats

** 题意：**有n个草排成一列，每个草有一个甜味值；有m头牛，每头牛有一个自己喜欢的甜味值f和饥饿程度h，意思是这头牛只吃这个甜味值的草，并且吃h个就会饱；你需要在这列草的左右确定两个牛的集合，你可以决定牛的前后顺序以及吃草的方向，牛吃草的原则如下： 每头牛确定了吃草方向后就只能向那个方向走； 每头牛只吃自己喜欢的甜味值的草，不是这个甜味值直接跳过； 每头牛在吃了h个草之后会就地睡在这个格子上； 如果一头牛遇到了睡着的牛或者走到尽头还是没有吃够它就会不高兴； 农夫想要选择尽可能多的牛使得他们都高兴，问你最大数量以及方案数（左右两个集合内元素不同就视为不同的方案）；

#include<bits/stdc++.h>
using namespace std;#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn = 1e4 + 10;
const int mod = 1e9 + 7;
int m, n, mx = 0;
int l[maxn], r[maxn], a[maxn];
vector<int> v[maxn];
ll ans = 0;
int main(){
    ios_base::sync_with_stdio(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        cin >> a[i];
    }
    for (int i = 1; i <= m; i++){
        int h, f;
        cin >> f >> h;
        v[f].push_back(h);
    }
    for (int i = 1; i <= n; i++){
        sort(v[i].begin(), v[i].end());
    }
    for (int i = 0; i <= n; i++){
        for (int j = 0; j <= n; j++){
            l[j] = r[j] = 0;
        }
        for (int j = 1; j <= i; j++){
            l[a[j]]++;
        }
        for (int j = i + 1; j <= n; j++){
            r[a[j]]++;
        }
        int ok = i == 0, num = i != 0;
        ll s = 1;
        for(auto x : v[a[i]]){
            if(x == l[a[i]]){
                ok = 1; break;
            }
        }

        if(!ok)  continue;

        for (int j = 1; j <= n; j++){
            int x = 0, y = 0, sz = v[j].size();
            while(x < sz && v[j][x] <= l[j]) x++;
            while(y < sz && v[j][y] <= r[j]) y++;
            if(j == a[i]){  
                x = 0;  y -= (r[j] >= l[j]);
            }
            if(x + y == 0) continue;
            if(x > y) swap(x, y);
            if(!x){
                num ++; s = s * y % mod;
            }
            else if(y == 1){
                num ++; s = s * 2 % mod;
            }
            else{
                num += 2; s = s * x * (y - 1) % mod;
            }
        }
        
        if(num > mx){
            mx = num; ans = 0;
        }
        if(num == mx){
            ans = (ans + s) % mod;
        }
    }

    cout << mx << " " << ans << endl;
    return 0;
}

https://link.zhihu.com/?target=https%3A//codeforces.com/contest/1767/problem/C

int n, a[105][105], f[105][105];
 
void slove() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = i; j <= n; j++)
            cin >> a[i][j];
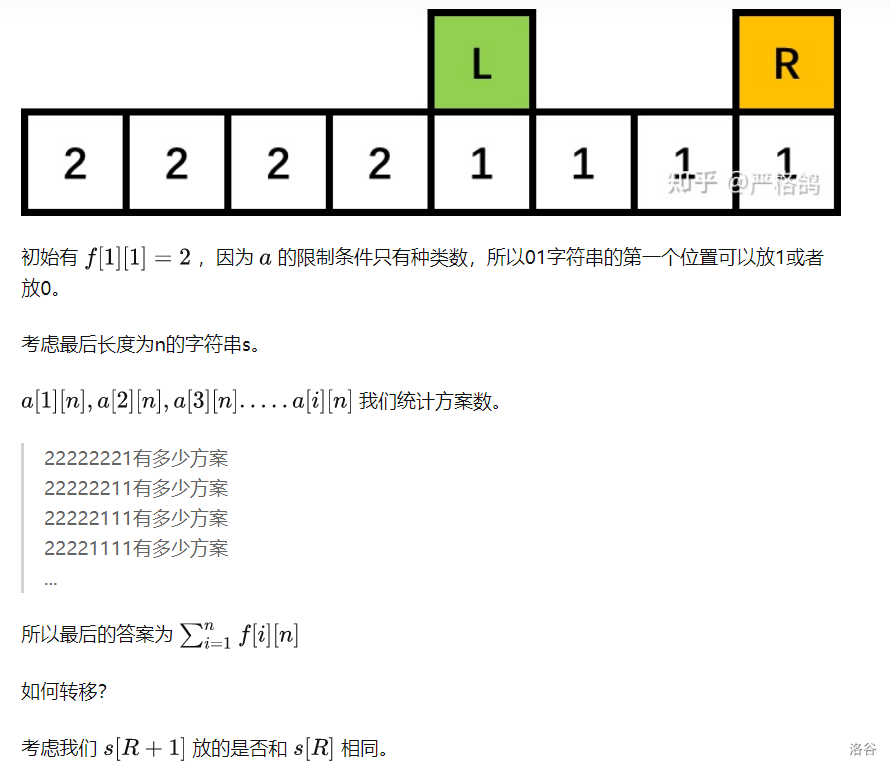
    f[1][1] = 2;
    for (int R = 1; R <= n; R++) {
        for (int L = 1; L <= R; L++) {
            bool flag = true;
            //            L       R
            //2 2 2 2 2 2 1 1 1 1 1
            for (int i = 1; i <= L - 1; i++)
                if (a[i][R] == 1)flag = false;//a[i][R]必须为 2/0 
            for (int i = L; i <= R; i++)
                if (a[i][R] == 2)flag = false;//a[i][R]必须为 1/0 
            if (!flag)f[L][R] = 0;
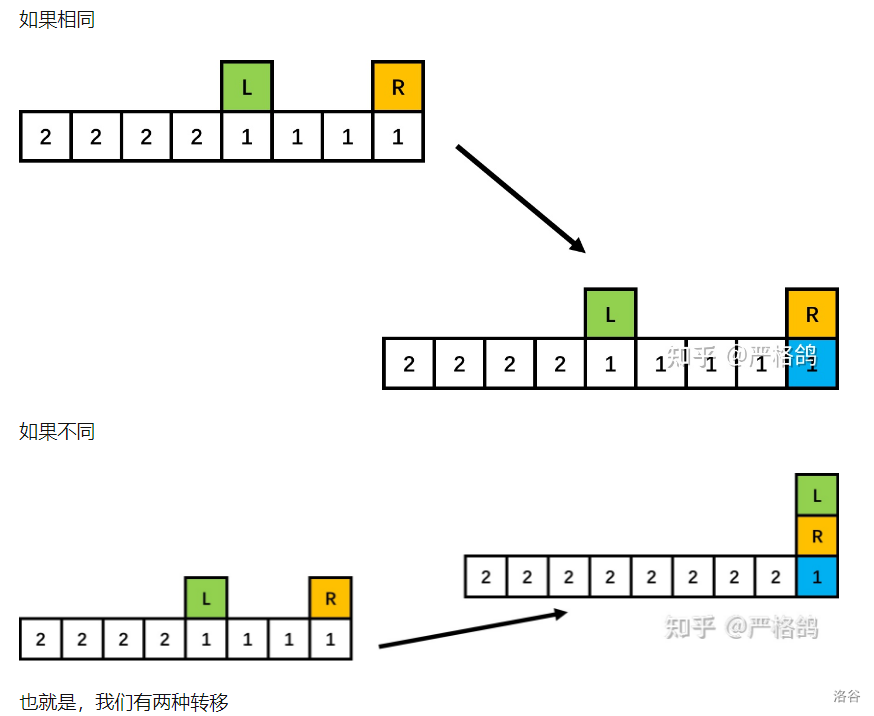
            (f[L][R + 1] += f[L][R]) %= mod;
            (f[R + 1][R + 1] += f[L][R]) %= mod;
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; i++)(ans += f[i][n]) %= mod;
    cout << ans << endl;
}