第 45 届国际大学生程序设计竞赛(ICPC)亚洲区域赛(昆明)
H Hard Calculation
签到题
J Parallel Sort

分析:很好想到找环 对于每个环 最多两次操作即可还原
构造每个环的方案 :每次将环脱去一对即可
开始我构造的按照顺序脱去一对 但是只过了70个点 正解为首尾依次脱环
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
struct huan
{
vector<int> sig;//环中数据的位置
int type;//环的型号,一元环为0,2元为1,更多为2
};
int maxtip = 0;//最大环型号
huan allh[100005];//环组
int aback = 0;//环组尾标
int orig[100005];//原始数据
int seat[100005];//i在原始数据中的位置
bool used[100005];//开环时被使用标记
int main()
{
int n; cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> orig[i];
seat[orig[i]] = i;
}
//打出所有环
for (int i = 1; i <= n; i++)
{
if (used[i] == 1)
continue;//已经入环的去掉
int t = aback;
aback++;//栈顶移动
allh[t].sig.push_back(i);//环的开头
used[i] = 1;
int j = orig[i];
while (1)
{
if (j != i)//不是环尾
{
allh[t].sig.push_back(j);
used[j] = 1;
j = orig[j];
}
else//是环尾
{
used[j] = 1;
break;//不进入,直接跳出
}
}
//给出类型
int size = allh[t].sig.size();
if (size == 1)
allh[t].type = 0;
else if(size == 2)
allh[t].type = 1;
else
allh[t].type = 2;
maxtip = max(maxtip, allh[t].type);
}
//输出结果
cout << maxtip << endl;
for (int i = maxtip; i > 0; i--)//每一行
{
vector<int> y;//装输出数据的数组
for (int j = 0; j < aback; j++)//遍历每个环
{
if (allh[j].type >= i)//只有等级足够的环才来
{
int right = allh[j].sig.size() - 1;
int left = i == 2 || allh[j].type == 1 ? 0 : 1;
while (left < right)
{
y.push_back(allh[j].sig[left]);
y.push_back(allh[j].sig[right]);
left++;
right--;
}
}
}
cout << y.size() / 2;
for (int k = 0; k < y.size(); k++)
{
cout << " " << y[k];
}
cout << endl;
}
}
L Simone and graph coloring

分析:考虑如果完全降序 整个图即为一个完全图 这样每个点的颜色都需要不同
所以想到对于每个下降子序列的长度就是所需颜色的数量 最长就是答案
至于方案数在求最长下降子序列的过程中跟新
需要用到二分dp来求解
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int T,n,a[N],b[N],ls[N];
int get(int l,int r,int x){
while(l<r){
int mid=(l+r)>>1;
if(ls[mid]>x) l=mid+1;
else r=mid;
}
return l;
}
void solve(){
int tot=0; cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
if(tot==0||a[i]<ls[tot]) ls[b[i]=++tot]=a[i];
else{
int tmp = get(1,tot,a[i]);
b[i] = tmp;
ls[tmp] = a[i];
}
}
cout<<tot<<"\n";
for(int i=1;i<=n;i++) cout<<b[i]<<" \n"[i==n];
}
int main(){
cin>>T;
while(T--) solve();
}
M Stone Games
题意:求静态区间数的选取集合不能构造出的和的最小值,在线
分析:
如果没有1,则凑不出来的最小数为1
否则设有x个1
显然,一定可以凑出[1,x]
注意到如果剩余大于1的数中最小数为k,若k<=x+1
则可以凑出[1,x+k]
推知若当前可以凑出[1,x],剩余数中所有小于等于x+1的数,均可累加到连续上限中
即凑出[1,x+Σsi(si<=x+1)]
若找不到新增的数,则答案为x+1。
主席树维护区间小于等于某个数的和,可以不初始化直接边插入边建树
#include <iostream>
#include <cstring>
#include <algorithm>
#define int long long
using namespace std;
const int N = 1e6+10,inf = 1e9;
int n,m,idx,root[N];
struct Node{
int l,r;
int sum;
}tr[N*50];
int insert(int p,int l,int r,int x){
int q=++idx;
tr[q]=tr[p];
if(l==r){
tr[q].sum+=x;
return q;
}
int mid=l+r>>1;
if(x<=mid) tr[q].l=insert(tr[p].l,l,mid,x);
else tr[q].r=insert(tr[p].r,mid+1,r,x);
tr[q].sum=tr[tr[q].l].sum+tr[tr[q].r].sum;
return q;
}
int query(int q,int p,int l,int r,int ql,int qr){
if(l>=ql&&r<=qr) return tr[q].sum-tr[p].sum;
if(l>qr||r<ql) return 0;
int mid=l+r>>1;
return query(tr[q].l,tr[p].l,l,mid,ql,qr)+query(tr[q].r,tr[p].r,mid+1,r,ql,qr);
}
signed main(){
cin>>n>>m;
for(int i=1,t;i<=n;i++){
cin>>t;
root[i]=insert(root[i-1],0,inf,t);
}
int res=0;
while(m--){
int l,r;
cin>>l>>r;
l=(res+l)%n+1,r=(res+r)%n+1;
if(l>r) swap(l,r);
int x=query(root[r],root[l-1],0,inf,1,1);
int last=x;
while(1){
int sum=query(root[r],root[l-1],0,inf,1,min(inf,x+1))-last;
if(!sum) break;
x+=sum,last=x;
}
res=x+1;
cout<<res<<endl;
}
return 0;
}
J Mr. Main and Windmills
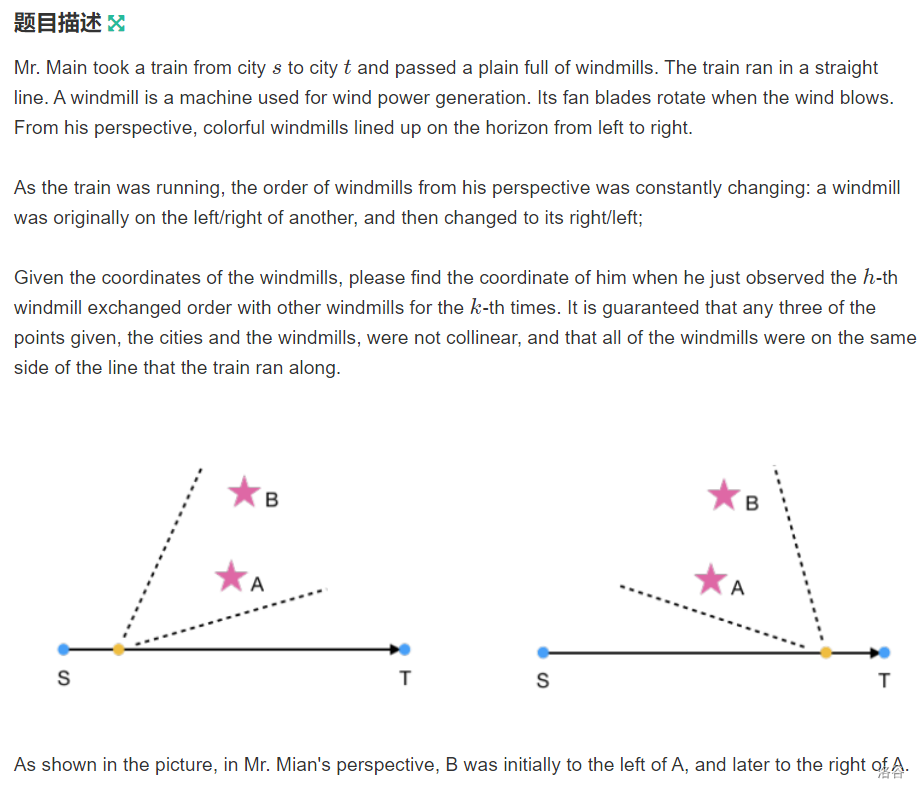
分析:就是暴力就好 计算几何不在我的范围类
#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
typedef long long LL;
LL x1,y1,x2,y2;
LL n,m;
struct node
{
LL x;
LL y;
}N[1001];
vector<double> V[1001];
int main()
{
cin>>n>>m;
cin>>x1>>y1>>x2>>y2;
for(int a=1;a<=n;a++) cin>>N[a].x>>N[a].y;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i!=j)
{
LL x3=N[i].x,y3=N[i].y,x4=N[j].x,y4=N[j].y;
double t1=(double)(x3 * (y4 - y3) + y1 * (x4 - x3) - y3 * (x4 - x3) - x1 * (y4 - y3)) / ((x2 - x1) * (y4 - y3) - (x4 - x3) * (y2 - y1));
if(t1>0&&t1<1) V[i].push_back(t1);
}
for(int a=1;a<=n;a++) sort(V[a].begin(),V[a].end());
while(m--)
{
int h,k;
cin>>h>>k;
if(k<=V[h].size()) printf("%.6f %.6f\n",x1+V[h][k-1]*(x2-x1),y1+V[h][k-1]*(y2-y1));
else cout<<-1<<"\n";
}
}
C Cities
题意:
给定长度为n的序列a 一次操作你可以选择一个数值相同的连续区间,将这个区间的数值修改为其他数。问多少进行多少次操作能使得区间所有数相同。
数据范围:n<=5000,每种a(i)最多出现15次
分析:
很明显的区间dp 关键是数据范围只允许15×n方 但是一般的区间dp范围时n三方
考虑将第三维 枚举中间断点的变成最多枚举十五次 想到维护每个数前面和她颜色一样的数的位置 用pre[i] 表示
首先对序列进行去重 这一步很关键!!!!
因为只有两端相同的情况下 才会使得区间答案变得更小
d[l][r]可以由多种状态转移更新:
1.首先用d[l+1][r]+1和a[l][r-1]+1更新,这个转移比较显然.
2.如果a[l]=a[r],那么可以用d[l+1][r-1]+1更新,将[l+1,r-1]变成相同,再变成a[r].
!!!!但是这样不一定是最优的 因为可能[l+1,r-1]开始就变成了a[r] 就不需要再花费1了 没关系取个min就好
首先明确 d[l][r] 如果a[l]=a[r] 最终这段区间一定是a[r] 如果a[l]!=a[r] 最终这段区间可能为区间内任何出现过的数 并且如果最终是a[l] 或者a[r]都是一样的
3.对于[l+1,r-1]中的位置k,如果满足a[k]=a[r],那么可以用d[l][k-1]+d[k][r]+1更新
4.对于[l+1,r-1]中的位置k,如果满足a[k]=a[r],同时a[l]=a[k],即a[l]=a[k]=a[r]
那么可以用d[l][k-1]+d[k][r]更新,即将[l,k-1]和[k+1,r]都变成a[k].
最后d[1][n]就是答案.
说难也不难 说简单也真不简单
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=5e3+5;
int n,cnt;
int dp[maxn][maxn],a[maxn],pre[maxn],mp[maxn];
void solve();
int main(){
int T;cin>>T;
while(T--)solve();
return 0;
}
void solve(){
cin>>n;cnt=0;
memset(dp,0,sizeof(dp));
memset(pre,0,sizeof(pre));
memset(mp,0,sizeof(mp));
//去重这一步非常很关键
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
if(a[i]!=a[i-1])
a[++cnt]=a[i];
else continue;
pre[cnt]=mp[a[i]];
mp[a[i]]=cnt;
}
for(int i=1;i<=cnt;i++)
for(int j=i;j<=cnt;j++)
dp[i][j]=j-i;
for(int len=2;len<=cnt;len++){
for(int l=1;l+len-1<=cnt;l++){
int r=l+len-1;
dp[l][r]=min(dp[l][r],min(dp[l+1][r],dp[l][r-1])+1);
if(a[l]==a[r])dp[l][r]=min(dp[l][r],dp[l+1][r-1]+1);
for(int k=pre[r];k>l;k=pre[k]){
dp[l][r]=min(dp[l][r],dp[l][k-1]+dp[k][r]+1);
if(a[l]==a[r])
dp[l][r]=min(dp[l][r],dp[l][k-1]+dp[k][r]);
}
}
}
cout<<dp[1][cnt]<<endl;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号