Codeforces Round #789 (Div. 2)

签到题没啥好说的

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=105;
int T;
int a[maxn];
void solve(); 
int main(){
	cin>>T;
	while(T--)solve();
     return 0;
}
void solve(){
	int n;
	int res=0;cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		if(a[i]==0)res++;
	}
	if(res)cout<<n-res<<endl;
	else{
		sort(a+1,a+1+n);
		bool pd=1;
		for(int i=1;i<=n;i++)
		if(a[i]==a[i-1])
		pd=0;
		if(pd)cout<<n+1<<endl;
		else cout<<n<<endl;
	}
}

好像可以贪心不过我一眼看去就直接写了dp

dp[i][j][k] 其中j为0/1表示当前为‘1’还是‘0’ k为0/1表示当前状态合法还是不合法

表示前i个 第i位置个为j 状态为k

合法一定是由不合法转移过来的 不合法只能从合法转移过来

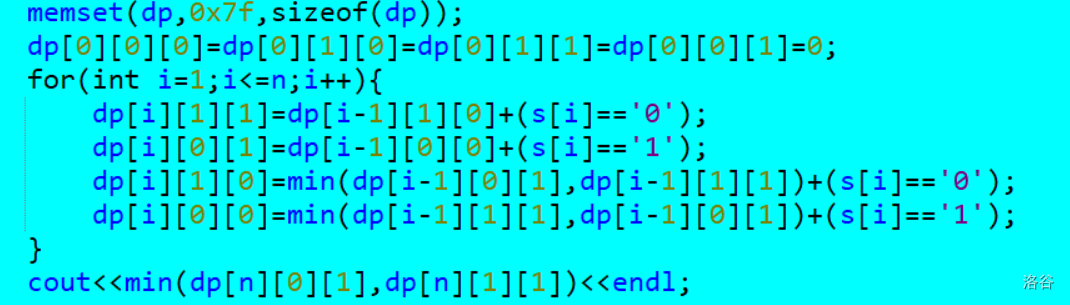
点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=2e5+5;
int dp[maxn][2][2];// [1][1]当前为1 合法 [1][0]当前为0 合法 [0][1] 当前为1 不合法 [0][0] 当前为0 不合法 
char s[maxn];
int T;
void solve();
int main(){
	cin>>T;
	while(T--)solve();
     return 0;
}
void solve(){
	int n;
	cin>>n;
	scanf("%s",s+1);
	memset(dp,0x7f,sizeof(dp));
	dp[0][0][0]=dp[0][1][0]=dp[0][1][1]=dp[0][0][1]=0;
	for(int i=1;i<=n;i++){
		dp[i][1][1]=dp[i-1][1][0]+(s[i]=='0');
		dp[i][0][1]=dp[i-1][0][0]+(s[i]=='1');
		dp[i][1][0]=min(dp[i-1][0][1],dp[i-1][1][1])+(s[i]=='0');
		dp[i][0][0]=min(dp[i-1][1][1],dp[i-1][0][1])+(s[i]=='1');
	}
	cout<<min(dp[n][0][1],dp[n][1][1])<<endl;
}

这个题就上一个题目的加强版 我们只需要在转移的时候顺便记录一下就好

这个题要用双线并行 卡常数 没啥意思 我下面的代码TLE了

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=2e5+5;
int dp[maxn][2][2],num[maxn][2][2];
// [1][1]当前为1 合法 [1][0]当前为0 合法 [0][1] 当前为1 不合法 [0][0] 当前为0 不合法 
char s[maxn];
int T,res;
void solve();
int main(){
	scanf("%d",&T);
	while(T--)solve();
     return 0;
}
void solve(){
	int n;
	scanf("%d",&n);
	scanf("%s",s+1);
	memset(dp,0x7f,sizeof(dp));
	memset(num,0,sizeof(num));
	dp[0][0][0]=dp[0][1][0]=dp[0][1][1]=dp[0][0][1]=0;
	for(int i=1;i<=n;i++){
		dp[i][1][1]=dp[i-1][1][0]+(s[i]=='0');
		num[i][1][1]=num[i-1][1][0];
		dp[i][0][1]=dp[i-1][0][0]+(s[i]=='1');
		num[i][0][1]=num[i-1][0][0];
		if(dp[i-1][0][1]<dp[i-1][1][1])
		num[i][1][0]=num[i-1][0][1]+1,dp[i][1][0]=dp[i-1][0][1]+(s[i]=='0');
		else num[i][1][0]=num[i-1][1][1],dp[i][1][0]=dp[i-1][1][1]+(s[i]=='0');
		if(dp[i-1][1][1]<dp[i-1][0][1])
		num[i][0][0]=num[i-1][1][1]+1,dp[i][0][0]=dp[i-1][1][1]+(s[i]=='1');
		else num[i][0][0]=num[i-1][0][1],dp[i][0][0]=dp[i-1][0][1]+(s[i]=='1');
	}
	if(dp[n][0][1]<dp[n][1][1])
	res=num[n][0][1];
	else res=num[n][1][1];
	printf("%d %d\n",min(dp[n][0][1],dp[n][1][1]),res+1);
}

开始我想差分树状数组去维护 但是发现有一左一右两个限制 应该是可以维护出来的 但是我不知道怎么维护

像这种题其实就是先定一边 再计算

考虑先枚举断点i 穿过i的区间很好计算 但是没有穿过的呢？

我们只要依次处理右边为断点i的就好

描述不好描述 代码一看就能明白 这个题的解题思路很牛逼

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int maxn=5e3+5;
int T;
ll dp[maxn],a[maxn],pre[maxn];
void solve();
int main(){
	cin>>T;
	while(T--)solve();
     return 0;
}
void solve(){
	int n;cin>>n;
	ll res=0;
	for(int i=1;i<=n;i++)scanf("%lld",&a[i]);
	for(int i=1;i<n;i++)
	for(int j=i+1;j<=n;j++)
	if(a[i]>a[j])dp[i]++;
	for(int i=1;i<=n;i++){
		for(int j=1;j<i;j++)
		if(a[j]>a[i])dp[j]--;
		pre[0]=0;
		for(int j=1;j<i;j++)pre[j]=pre[j-1]+dp[j];
		for(int j=1;j<i;j++)
		if(a[j]<a[i])
		res+=(pre[i-1]-pre[j]);
	}
	cout<<res<<endl;
}