构造专题

当时做的时候感觉快要搞出来了的 但是最后还是没有

向鱼骨一样错开，比如
111110 000001
100000 111111
111110 000001
100000 111111
111110 000001

首先这样能保证合并之后全图都是0 考虑如果该点强制是1 那么该点是0的矩阵就变成1就好 这个1可以和上一行或者下一行相连

这个构造属实巧妙 奇偶交错 这样保证在改变一个矩阵的情况下一定不会改变另一矩阵

点击查看代码

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int maxn=700;
char c[maxn][maxn];
char a[maxn][maxn];
char b[maxn][maxn];
int main()
{
	int n,m;
	cin>>n>>m;
	char ch=getchar(); 
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>c[i][j];
		}
		ch=getchar(); 
	}
	for(int i=1;i<=n;i++)
	{
		int ans=0;
		for(int j=1;j<=m;j++)
		{
			if(i==1||i==n||j==1||j==m)
			{
				a[i][j]='1';
				continue;
			}
			if(c[i][j]=='1')
			{
				ans++;
				a[i][j]='1';
			} 
				
		}
		
		if(ans&&i%2==1)
		{
			for(int j=2;j<m;j++)
				a[i][j]='1';
		}
		else 
		{
			for(int j=2;j<m;j++)
			if(a[i][j]!='1')
				a[i][j]='0';
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(c[i][j]=='1')b[i][j]='1';
			else if(a[i][j]=='1')b[i][j]='0';
			else b[i][j]='1';
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cout<<a[i][j];
		} 
		cout<<endl;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cout<<b[i][j];
		} 
		cout<<endl;
	}
}

题目大意：

给你k个方案数，让你构树

每个点有白色和黑色

并且如果树上有个点是黑色的那么它的子树也是黑色的

给出符合要求有k中方案的树

首先观察规律

一个点的方案数=（它所有的子树方案数的累乘+1）

然后如果是没有子树的点那么它的方案数就是2

一般构造就是分奇偶性的 ！！！！！

如果是目前方案数是奇数

我们就拆成两个子树，方案数就变一半了

因为有一个子树是单独一个点，而该点的方案数就是2

对另一个子树再进行相同操作

如果目前方案数是偶数的

我们就让他连上一个点，让他变成奇数，这时候方案数-1

（因为子树就一个嘛，子树累乘+1就是方案数）

注意边界情况 因为每次是奇数的时候我们在已经设置了两个节点 (一个节点是2 另一个节点是一个子树的根)

如果剩下k=2了 那么就不再需要加了 如果k=3 就只需要再加一个节点

点击查看代码

#include <bits/stdc++.h>

using namespace std;
pair<int,int>a[100010];
int ans=0;
int cnt=1;
int main()
{
    long long k=0;
    cin>>k;
    while(k){
        if(k==2)break;
        if(k==3){
            a[++ans]={cnt,cnt+1};
            cnt++;
            break;
        }
        if(k&1){
            a[++ans]={cnt,cnt+1};
            a[++ans]={cnt,cnt+2};
            cnt+=2;
            k=k/2;
            continue;
        }
        a[++ans]={cnt,cnt+1};
        cnt++;
        k--;
    }
    cout<<cnt<<endl;
    for(int i=1;i<=ans;i++){
        cout<<a[i].first<<' '<<a[i].second<<endl;
    }
    return 0;
}

题目：昆明ICPC Divisions：

链接：https://ac.nowcoder.com/acm/contest/32708/D

分析：

性质1： 如果S所有的数都相同 那么分法为 pow（2，n）即每个数可以在第一个集合或者第二个集合

性质2：如果构造单调不减的序列 如 1 1 2 2 2 3 3

不管怎么取 S1一定是符合题意的 但是S2必须只能取一种数 或 不取

所以取法为 pow(2,2)-1 + pow(2,3)-1 +pow(2,2)-1 +1 最后一个＋1为所有都不取的情况

这样依次构造就好 注意k=0并不是-1 比如 1 2 1 3 1 2

code:

#include<bits/stdc++.h>
using namespace std;
int ksm[30];
vector<int>a;
int main()
{
	int k;
    cin>>k;
    if(k==0){
    	cout<<6<<endl<<"1 2 1 3 1 2"<<endl;
	}
	else if(k==1){
		cout<<6<<endl<<"1 1 4 5 1 4"<<endl;
	}
    else{
    	k--;
    	ksm[0]=1;
    	for(int i=1;i<=29;i++)
    	ksm[i]=ksm[i-1]*2;
    	int cnt=0,i;
	while(k){
		i=1;
		while(ksm[i]-1<=k)i++;
		i--;++cnt;
		for(int j=1;j<=i;j++)
		a.push_back(cnt);
		k-=(ksm[i]-1);
	} 
	cout<<a.size()<<endl;
	for(int i=0;i<a.size();i++)cout<<a[i]<<" ";
    }
    return 0; 
}

https://codeforces.com/contest/1689/problem/E

int lowbit(int x) { return (x)&(-x); }
int n, a[2005], ans;
bool check() {
    UF uf = UF(30);
    int OR = 0;
    for (int i = 1; i <= n; i++)OR |= a[i];
    for (int i = 1; i <= n; i++) {
        int last = -1;
        for (int j = 0; j <= 30; j++) {
            if ((a[i] >> j) & 1) {
                if (last != -1)uf.Union(j, last);
                last = j;
            }
        }
    }
    set<int>st;
    for (int i = 0; i <= 30; i++) {
        if ((OR >> i) & 1)st.insert(uf.findFather(i));
    }
    return st.size() == 1;
}
void show() {
    cout << ans << endl;
    for (int i = 1; i <= n; i++)cout << a[i] << " ";
    cout << endl;
}
void slove() {
    ans = 0;
    cin >> n;
    int mxbit = 0;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        if (a[i] == 0)ans++, a[i] = 1;
        mxbit = max(mxbit, lowbit(a[i]));
    }
    if (check()) { show(); return; };
    ans++;
    for (int i = 1; i <= n; i++) {
        if (a[i] == 1)continue;
        a[i]--;
        if (check()) { show(); return; };
        a[i]++;
    }
    for (int i = 1; i <= n; i++) {
        a[i]++;
        if (check()) { show(); return; };
        a[i]--;
    }
    ans++;
    for (int i = 1; i <= n; i++)
        if (lowbit(a[i]) == mxbit) { a[i]--; break; }
    for (int i = 1; i <= n; i++)
        if (lowbit(a[i]) == mxbit) { a[i]++; break; }
    show();
}

https://ac.nowcoder.com/acm/contest/49888/E

分析：

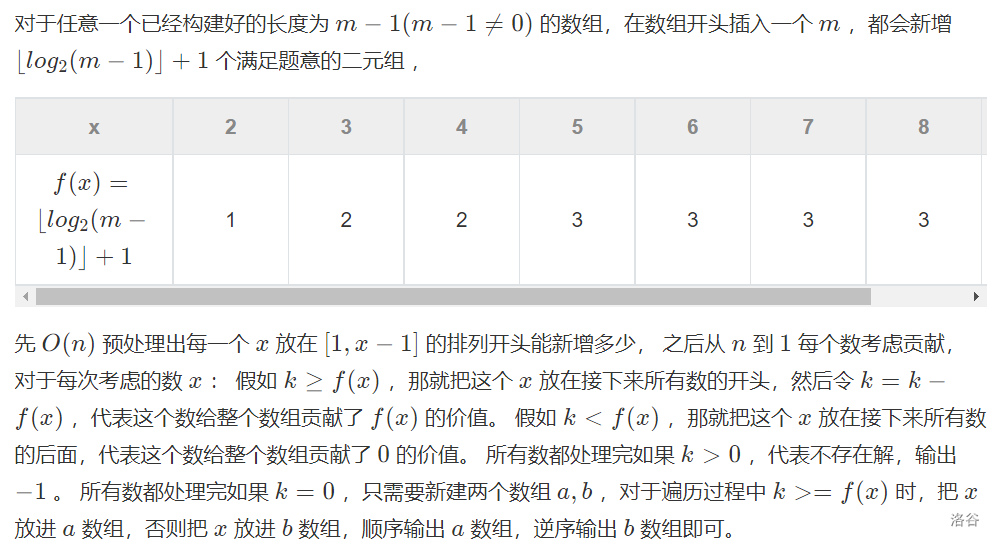
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,f[N];
int k;
vector<int>a,b;
int main(){
    cin>>n>>k;
    int now=1;
    for(int i=2;i<=n;i++){
        f[i]=f[i-1];
        if(i-1==now) {
            f[i]++;
            now*=2;
        }
    }
    for(int i=n;i>=1;i--){
        if(k>=f[i]) {
            a.push_back(i);
            k-=f[i];
        }else b.push_back(i);
    }
    if(k) cout<<"-1";
    else {
        reverse(b.begin(),b.end());
        for (auto i:a) cout << i << " ";
        for (auto i:b) cout << i << " ";
    }
    return 0;
}

https://codeforces.com/contest/1783/problem/B

题意：

请构造一个长宽为n的矩阵，要求矩阵内所有的数字是[1,n×n]的排列，且要求矩阵内每两个相邻数之间的绝对值之差的种类数量最多，输出该矩阵。

分析：

先不考虑将这n×n个数放入矩阵中

最多产生的差值也就n×n-1个

尽管每个格子与之四个格子相邻

但是构造的时候我们只需要保证每个格子只要满足相邻一个即可

例如n=4的时候 不难想到构造 1 16 2 15 ...这样一大一小的构造

为了使得构造的序列连续 不难想到蛇形构造

 void solve()
 {
     cin >> n;
     int l = 1, r = n * n;
     int cnt = 0;
     for (int i = 1; i <= n; i++ ) {
         if ((i & 1)) {
             for (int j = 1; j <= n; j++ , cnt++ ) {
                 if (cnt & 1) ans[i][j] = r--;
                 else ans[i][j] = l++;
             }
         } else {
             for (int j = n; j >= 1; j--, cnt++ ) {
                 if (cnt & 1) ans[i][j] = r--;
                 else ans[i][j] = l++;
             }
         }
     }
     
     for (int i = 1; i <= n; i++ ) 
         for (int j = 1; j <= n; j++ ) 
             cout << ans[i][j] << " \n"[j == n];
 }