计数专题

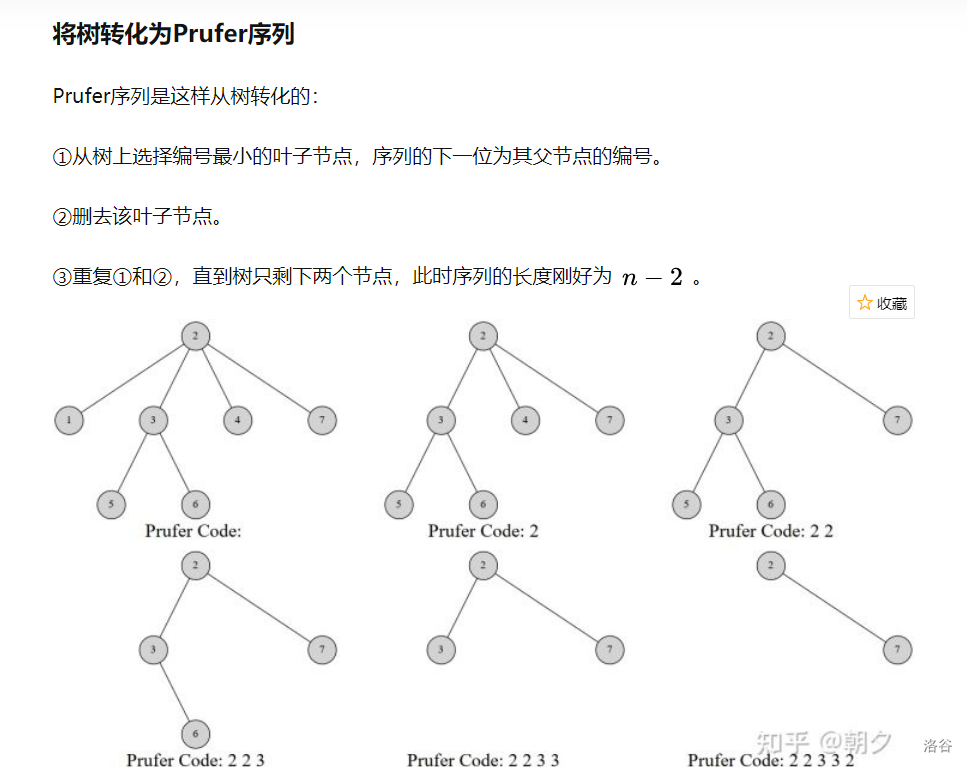
很明显可以用小根堆来处理 但是数据范围不允许
考虑线性想法 这个做法很好很实用
针对每次维护最小的且每次最多增加一个最小 都可以用这样的方法 !!!!完全可以替代小根堆

最后pufer转化为树反过来就好了 思路是一样的
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define int ll
#define ll long long
const int maxn=5e6+5;
int cnt;
int a[maxn],ans[maxn],in[maxn];
int n,c;
signed main(){
cin>>n>>c;
if(c==1){
for(int i=1;i<=n-1;i++)cin>>a[i],in[a[i]]++;
int minn;
for(int i=1;i<=n-1;i++)
if(!in[i]){
minn=i;break;
}
int now=minn;
while(cnt<n-2){
ans[++cnt]=a[now];
in[a[now]]--;
if(!in[a[now]]&&a[now]<minn)now=a[now];
else{
minn++;
while(in[minn])minn++;
now=minn;
}
}
int res=0;
for(int i=1;i<=n-2;i++)
res^=(i*ans[i]);
cout<<res;
}else{
for(int i=1;i<=n-2;i++)cin>>a[i],in[a[i]]++;
a[n-1]=n;in[n]++;
int minn;
for(int i=1;i<=n-1;i++)
if(!in[i]){
minn=i;break;
}
int now=minn;
for(int i=1;i<=n-1;i++){
ans[now]=a[i];
in[a[i]]--;
if(!in[a[i]]&&a[i]<minn)now=a[i];
else{
minn++;
while(in[minn])minn++;
now=minn;
}
}
int res=0;
for(int i=1;i<=n-1;i++)
res^=(i*ans[i]);
cout<<res;
}
return 0;
}

https://www.luogu.com.cn/problem/P2290 就是一道经典的板子题

题目要求完全二分图个数 考虑从完全图来推 完全图pufer会剩下两个点 到完全二分图这里这两个点一定是分居一边
一边的一个点一定有出边连向另一边 如果一一对应的话就是分别有n-1个和m-1个
选n-1次有m个选择方案 选m-1个有n个选择方案 所以答案就是ksm(n-1,m)× ksm(m-1,n)
注意long long 相乘可能会爆 所以要用到快速乘
点击查看代码
#include<cstdio>
typedef long long ll;
typedef long double ld;
ll n,m,p;
ll mul(ll a,ll b){
ll res=0;
while(b){
if(b&1)res=(res+a)%p;
b>>=1;a=a*2%p;
}
return res;
}
ll ksm(ll a,ll b)
{
ll ret=1;
for(;b;b>>=1,a=mul(a,a))
if(b&1) ret=mul(ret,a);
return ret;
}
int main()
{
scanf("%lld%lld%lld",&n,&m,&p);
printf("%lld\n",mul(ksm(n,m-1),ksm(m,n-1)));
}



点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define ull unsigned long long
#define met(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for(int i = a; i <= b; i++)
#define bep(i, a, b) for(int i = a; i >= b; i--)
#define re return 0
using namespace std;
const ll mod = 1e9 + 7;
const double PI = acos(-1);
const ll INF = 2e18+1;
const int inf = 1e9 + 15;
const double eps = 1e-7;
const int maxn = 1e6 + 5;
ll d[3003][3003], p[3003][3003];
string ma[3003];
int main(){
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
int n, m; cin >> n >> m;
n--, m--;
rep(i, 0, n) cin >> ma[i];
d[0][0] = p[0][0] = 1;
rep(i, 0, n){
rep(j, 1, m){
if(ma[i][j] == '.'){
if(i) d[i][j] += d[i-1][j];
if(j) d[i][j] += d[i][j-1];
d[i][j] %= mod;
}
}
}
rep(i, 1, n){
rep(j, 0, m){
if(ma[i][j] == '.'){
if(i) p[i][j] += p[i-1][j];
if(j) p[i][j] += p[i][j-1];
p[i][j] %= mod;
}
}
}
cout << ((d[n-1][m]*p[n][m-1])%mod - (d[n][m-1]*p[n-1][m])%mod + mod) % mod << endl;
re;
}


这个题目平移一条直线让我想到了卡特兰数
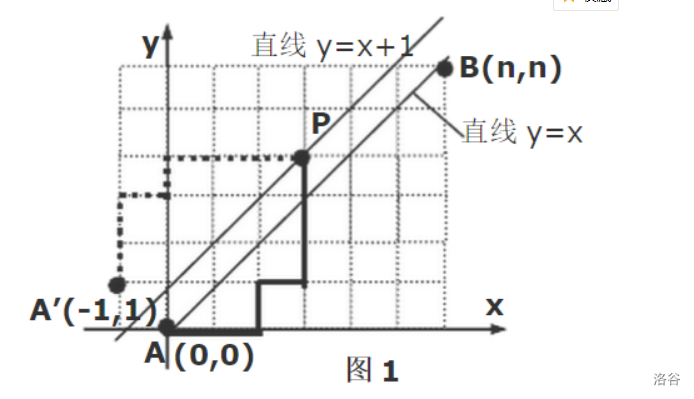
跨过y=x的线就相当于到了y=x+1的线 再对称一下就是(-1,1)到(n,n)
下面的链接讲得很详细
https://www.cnblogs.com/wzxbeliever/p/11686144.html

叶子期望=(各个情况叶子总和)/各个情况
难点就在于怎么算出各个情况下叶子总数
对于每棵n个点的二叉树,如果里面有k个叶节点,那么我们分别把这k个叶子删去会得到k棵n−1个点的二叉树;
而每棵n−1个点的二叉树恰好有n个位置可以悬挂一个新的叶子,所以每棵n−1个点的二叉树被得到了n次;
这个是实验出来的 我也不知道怎么推 不过确实神奇
综上,我们即可得出结论:所有n个点的二叉树的叶子个数和等于n-1个点的二叉树个数×n。

这个题是卡特兰数另一个金典的公式的几何形态



一个点的度数为d 在prufer序列中出现的次数是d-1 每个点度数的价值可以预处理出来
总容量n-2 但是有n个点的价值是要计算的 因为有些点的度数是1 容量为0 不会出现在prufer序列当中 但是该价值任然要计算的
一般的背包是没法处理的 可以多开一维 但是复杂度不允许 考虑对每个点的价值都-f(1) 最后减了多少个f(1)就是选了多少个度数不为1的点
最后加上n个度数为1的点的价值 就是最终的答案 很巧妙!!!!
杨老师的照相排列:
链接:https://www.acwing.com/problem/content/273/
标签是个简单题 想了半天还是去看了题解 我还是太菜了
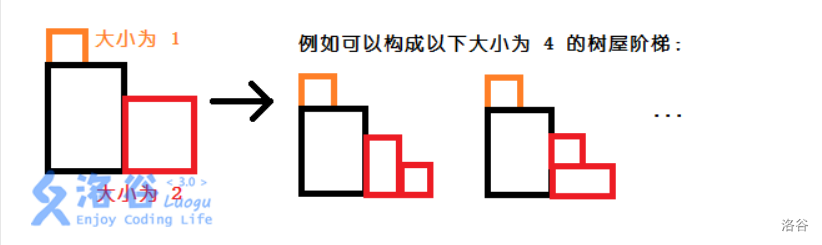
这是个非常经典的dp 想一下怎么摆放满足条件 这样类型的题目一般都是从大到小(从小到大)开始摆放
不难想到我们只要摆放的时候一直满足一个阶梯形状 就满足条件 因为我们是从大到小放的
code:
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int a[6];
ll dp[32][32][32][32][32];
int main(){
int k;
scanf("%d",&k);
while(k){
memset(dp,0,sizeof(dp));
dp[0][0][0][0][0]=1;
memset(a,0,sizeof(a));
for(int i=1;i<=k;i++)scanf("%d",&a[i]);
for(int i=0;i<=a[1];i++)
for(int j=0;j<=a[2];j++)
for(int k=0;k<=a[3];k++)
for(int l=0;l<=a[4];l++)
for(int m=0;m<=a[5];m++){
if(i<a[1])dp[i+1][j][k][l][m]+=dp[i][j][k][l][m];
if(j<a[2]&&j<i)dp[i][j+1][k][l][m]+=dp[i][j][k][l][m];
if(k<a[3]&&k<j)dp[i][j][k+1][l][m]+=dp[i][j][k][l][m];
if(l<a[4]&&l<k)dp[i][j][k][l+1][m]+=dp[i][j][k][l][m];
if(m<a[5]&&m<l)dp[i][j][k][l][m+1]+=dp[i][j][k][l][m];
}
cout<<dp[a[1]][a[2]][a[3]][a[4]][a[5]]<<endl;
scanf("%d",&k);
}
return 0;
}
https://www.luogu.com.cn/problem/P2606
分析;又是一个与排列有关的计数题,
P(i)>P(i/2)这个条件很重要啊
也有P(2*i)>P(i),
也有P(2*i+1)>P(i)
像这种下标二倍的关系就要和二叉树考虑在一起
二叉树:i的左儿子就是2*i,i的右儿子就是2*i+1
而且这颗二叉树是个完全二叉树
线性求完全二叉树的方案数 一颗完全二叉树 的左子树和右子树一定分别为完全为二叉树
所以左右子树的大小是一定的
根节点的值必须为最小值。再考虑剩下的i-1个节点。
很容易想到,
可以在这i-1个节点中选出l个节点作为左子树,剩下的r个节点作为右子树。所以得出转移:
f[i]=C(i-1,l)×f[l]×f[r]
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
inline int read() {
int res = 0; bool bo = 0; char c;
while (((c = getchar()) < '0' || c > '9') && c != '-');
if (c == '-') bo = 1; else res = c - 48;
while ((c = getchar()) >= '0' && c <= '9')
res = (res << 3) + (res << 1) + (c - 48);
return bo ? ~res + 1 : res;
}
const int N = 1e6 + 5;
int n, PYZ, f[N], fac[N], Log[N], inv[N];
int qpow(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = 1ll * res * a % PYZ;
a = 1ll * a * a % PYZ;
b >>= 1;
}
return res;
}
int C(int x, int y) {
if (!y) return 1;
int u = C(x / PYZ, y / PYZ), v = x % PYZ, w = y % PYZ, z;
if (v < w) z = 0;
else z = 1ll * (1ll * fac[v] * inv[w] % PYZ) * inv[v - w] % PYZ;
return 1ll * u * z % PYZ;
}
int main() {
int i, kx, l = 1, r = 1; n = read(); PYZ = read();
fac[0] = 1; Log[0] = -1;
for (i = 1; i <= n; i++) fac[i] = 1ll * fac[i - 1] * i % PYZ,
Log[i] = Log[i >> 1] + 1;
kx = min(PYZ - 1, n); inv[kx] = qpow(fac[kx], PYZ - 2);
for (i = kx - 1; i >= 0; i--) inv[i] = 1ll * inv[i + 1] * (i + 1) % PYZ;
f[1] = f[2] = 1; f[3] = 2;
for (i = 4; i <= n; i++) {
if (i - (1 << Log[i]) + 1 <= (1 << Log[i] - 1)) l++;
else r++;
f[i] = 1ll * (1ll * C(i - 1, l) * f[l] % PYZ) * f[r] % PYZ;
}
printf("%d\n", f[n]);
return 0;
}
https://www.luogu.com.cn/problem/P1370
题目大意:Σ(1<=l<=r<=n)F(l, r),其中F(l,r)表示[l,r]之间的本质不同的子序列有多少个
分析:
如果本题数据是N2的话我就会做,但是要求是O(n)求出
同样的区间计数题,固定端点L,再考虑dp
设dp[i]表示F[i,i]+F[i,i+1]+F[i,i+2]+....+F[i,n]
如果没有重复的数字话
dp[i]=(dp[i+1]<<1)+2
但是有重复怎么办?考虑容斥
若ai==aj(i<j)
则dp[i]-=dp[j+1]+1;
原因是 后面所有的F[j+1,j+1].....都会有一次重复(接ai,接aj)
那个1就是F[j,j]中选j或不选j中的选j的方案
并且j是i后面第一个与ai相同的位置
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 998244353
#ifdef ONLINE_JUDGE
char *TT,*mo,but[(1<<15)+2];
#define getchar() ((TT==mo&&(mo=(TT=but)+fread(but,1,1<<15,stdin)),TT==mo)?0:*TT++)
#endif
inline int read(){
int x=0,c=0,f=1;
for(;c<'0'||c>'9';c=getchar())f=c!='-';
for(;c>='0'&&c<='9';c=getchar())x=x*10+c-'0';
return f?x:-x;
}
int head[100010];
int a[100010],b[100010];
ll dp[100010];
ll ans;
int n;
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
b[i]=a[i];
}
sort(b+1,b+n+1);
int cnt=unique(b+1,b+n+1)-b-1;
for(int i=1;i<=n;i++)a[i]=lower_bound(b+1,b+cnt+1,a[i])-b;
dp[n]=2;
head[a[n]]=n;
for(int i=n-1;i>0;i--){
dp[i]=(dp[i+1]*2+2)%mod;
if(head[a[i]]){
dp[i]=(dp[i]-dp[head[a[i]]+1]+mod-1)%mod;
head[a[i]]=i;
}
head[a[i]]=i;
}
for(int i=1;i<=n;i++){
ans=(ans+dp[i])%mod;
}
cout<<ans;
return 0;
}
链接:https://ac.nowcoder.com/acm/problem/13611
题目描述
shy有一颗树,树有n个结点。有k种不同颜色的染料给树染色。一个染色方案是合法的,当且仅当对于所有相同颜色的点对(x,y),x到y的路径上的所有点的颜色都要与x和y相同。请统计方案数。
分析:有两种做法 一种是讲树转化为dfs序(一般两点之间的路径都是这样) 变为线性dp
还有一种做法就是计数

#include <bits/stdc++.h>
using namespace std;
static auto faster_iostream = []() { ios::sync_with_stdio(0); cin.tie(0); return 0; }();
typedef long long ll;
const int N = 1e3 + 5, M = 1e9 + 7;
ll qpow(ll x, ll n) { ll res = 1; for (; n; n >>= 1, x = x * x % M) if (n & 1) res = res * x % M; return res; }
ll fac[N];
ll comb(ll n, ll m) {
return fac[n] * qpow(fac[m] * fac[n-m] % M, M - 2) % M;
}
int main() {
int n, k;
cin >> n >> k;
fac[0] = fac[1] = 1;
for (int i = 2; i <= max(n, k); i++) {
fac[i] = fac[i-1] * i % M;
}
ll ans = 0;
for (int i = 0; i <= min(n - 1, k - 1); i++) {
ans += comb(n - 1, i) * comb(k, i + 1) % M * fac[i + 1] % M;
ans %= M;
}
cout << ans << '\n';
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号