Educational Codeforces Round 57

签到题 输出l 和2l即可

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int T; 
int main(){
	cin>>T;
	while(T--){
		int l,r;
		cin>>l>>r;
		cout<<l<<" "<<2*l<<endl;
	}
     return 0;
}

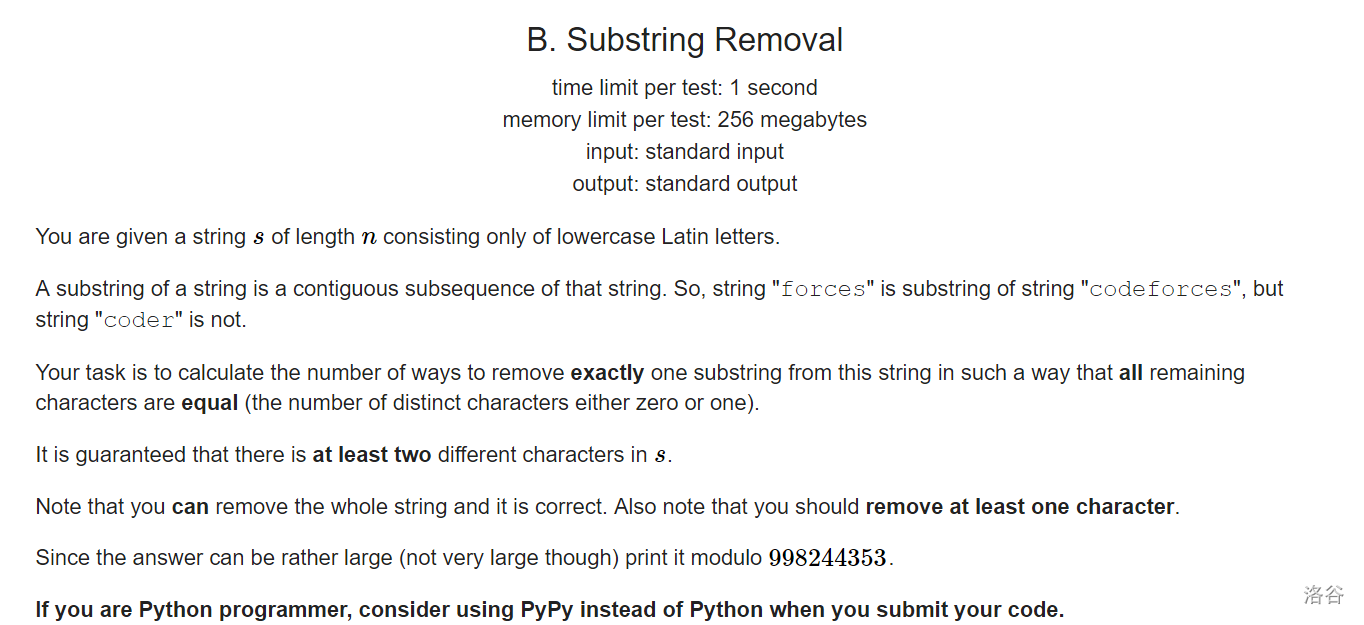
只用考虑前后两端就好

如果前后两端相同 (前端相同数+1)×（后端相同数+1）

如果前后两端不同 （前段相同数+1）+（后端相同数+1）-1

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
const int mod=998244353;
int n;
ll ans;
int main(){
	cin>>n;
	string s;
	cin>>s;
	char pre,edd;
	pre=s[0];
	edd=s[n-1];
	ll spre=0,sedd=0;
	for(int i=0;i<n;i++)
	if(s[i]==pre)spre++;
	else break;
	for(int i=n-1;i>=0;i--)
	if(s[i]==edd)sedd++;
	else break;
	if(pre!=edd){	
	    ans=spre+1+sedd+1-1;
		cout<<ans<<endl;
		return 0;
	}
	else 
		cout<<(spre+1)*(sedd+1)%mod<<endl;
	
     return 0;
}

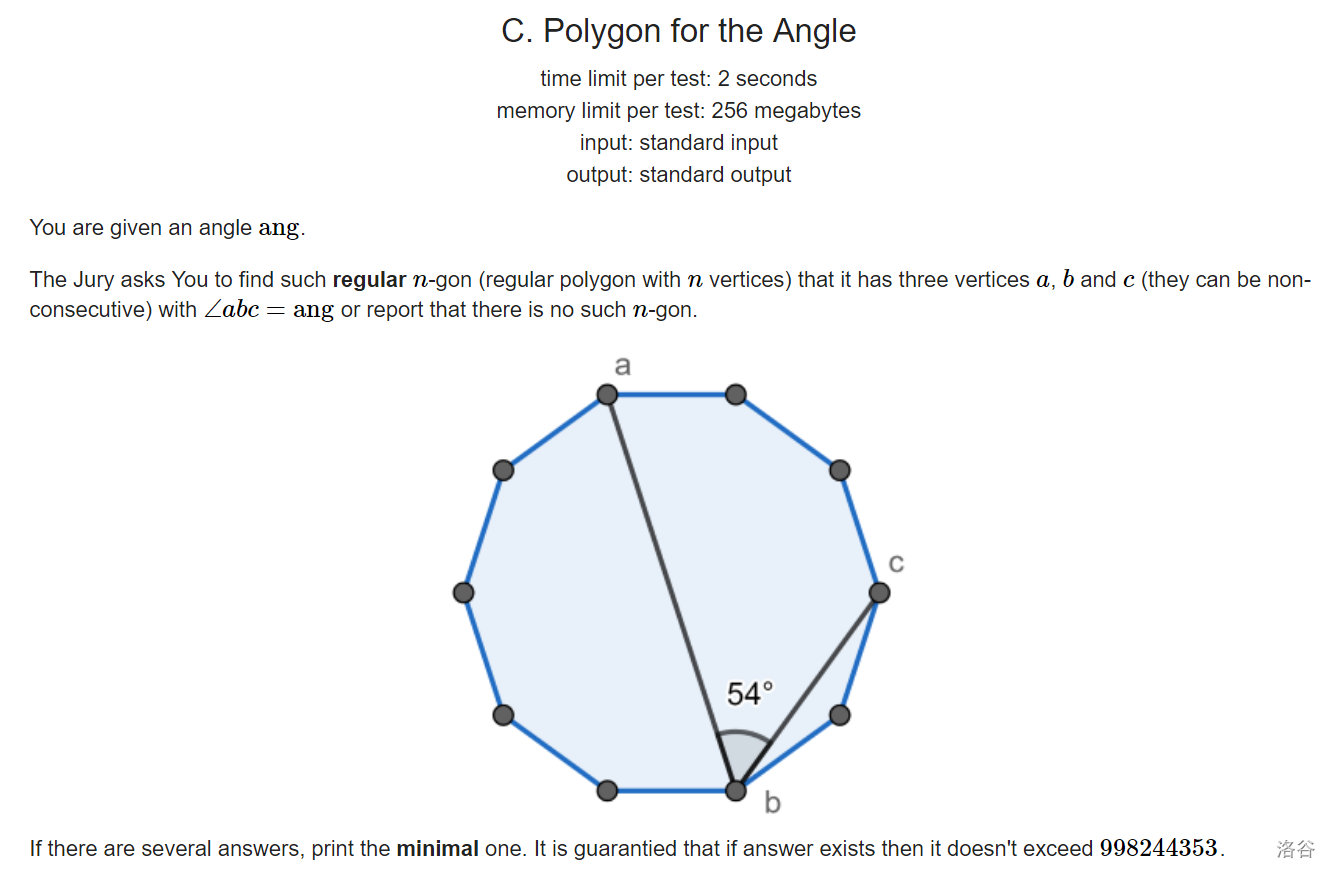
考虑每个n边形能形成的角度

对于每个n边形一个大角为 (180)×（n-2）/n

每个大角可以平均分为（n-2）个小角 每个小角为180/n 可以形成的角度为（180/n）×k 其中k属于 1到n-2

问题转化为 找到最小的n使得（180）× k = n × arg 其中k属于 1到n-2 即ax=by 的形式

求出gcd(a,b) x=b/gcd y=a/gcd 但是可能算出来k>=n-1 这样不满足范围限制 只要取次小的2*n就好

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int T;
int gcd(int a,int b){
	if(b)return gcd(b,a%b);
	return a;
}
int main(){
	cin>>T;
	while(T--){
		int arg;
		cin>>arg;
	    int gg=gcd(arg,180);
	    int k=arg/gg;
	    int n=180/gg;
	    if(k>=n-1)
	    cout<<n*2<<endl;
	    else cout<<n<<endl;
	}
     return 0;
}

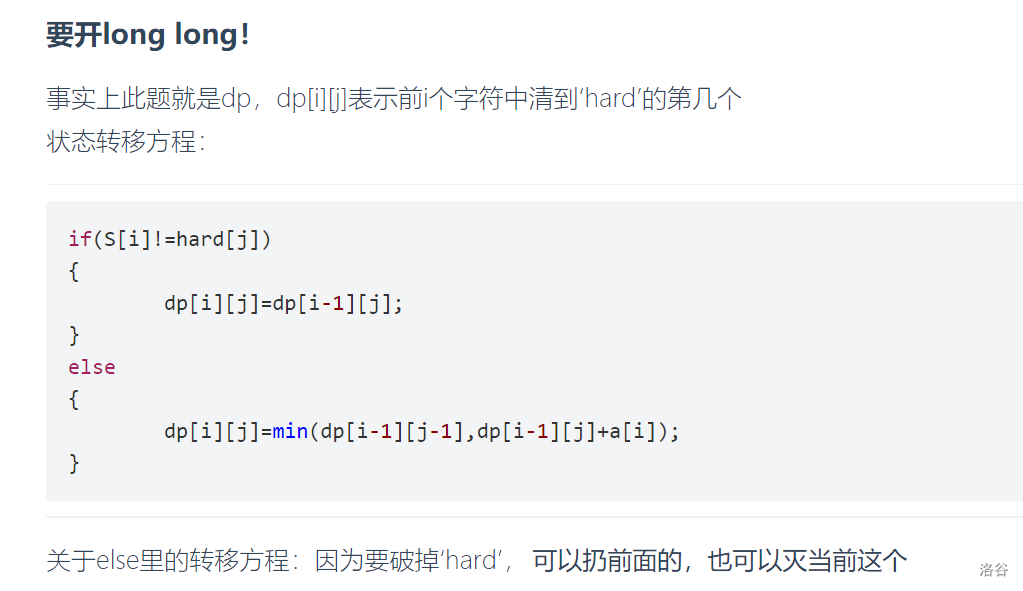
点击查看代码

#include<bits/stdc++.h>
using namespace std;
long long n,a[100010],dp[100010][10],ans;
char hard[5]={'\0','h','a','r','d'},S[100010];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>S[i];
	}
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
	}
	memset(dp,0x7f,sizeof(dp));
	for(int i=1;i<=4;i++)
	{
		dp[0][i]=0;
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=4;j++)
		{
			if(S[i]!=hard[j])
			{
				dp[i][j]=dp[i-1][j];
			}
			else
			{
				dp[i][j]=min(dp[i-1][j-1],dp[i-1][j]+a[i]);
			}
		}
	}
	ans=dp[n][1];
	for(int i=2;i<=4;i++)
	{
		if(dp[n][i]<ans)
		{
			ans=dp[n][i];
		}
	}
	cout<<ans;
}