条形均分纸牌和环形均分纸牌问题
条形:P1031 [NOIP2002 提高组] 均分纸牌

※第一堆牌相差的牌只能由第二堆牌承担(给予或索要)
※第一堆牌都达到要求了又去动它干嘛
※可以直接删除第一堆牌
※第二堆牌神奇的变成了第一堆牌
※重复上述操作
※如果当前牌没操作就已经达标了跳过啊~
※下副牌变成负数又怎么样?
※ ∵ 上述步骤皆可逆
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int n,a[101],mid,all,ans;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]),all+=a[i];
all/=n;
for(int i=1;i<=n;i++)if(a[i]-all)
a[i+1]+=a[i]-all,ans++;//如果是求传递纸牌的个数ans加abs(每组差值)就好
printf("%d",ans);
return 0;
}
环形:P2512 [HAOI2008]糖果传递
设Ai表示第i个小朋友原有的糖果数量,
ave表示所有小朋友糖果数量的平均数,
Xi表示第i个小朋友向左传的糖果数量。

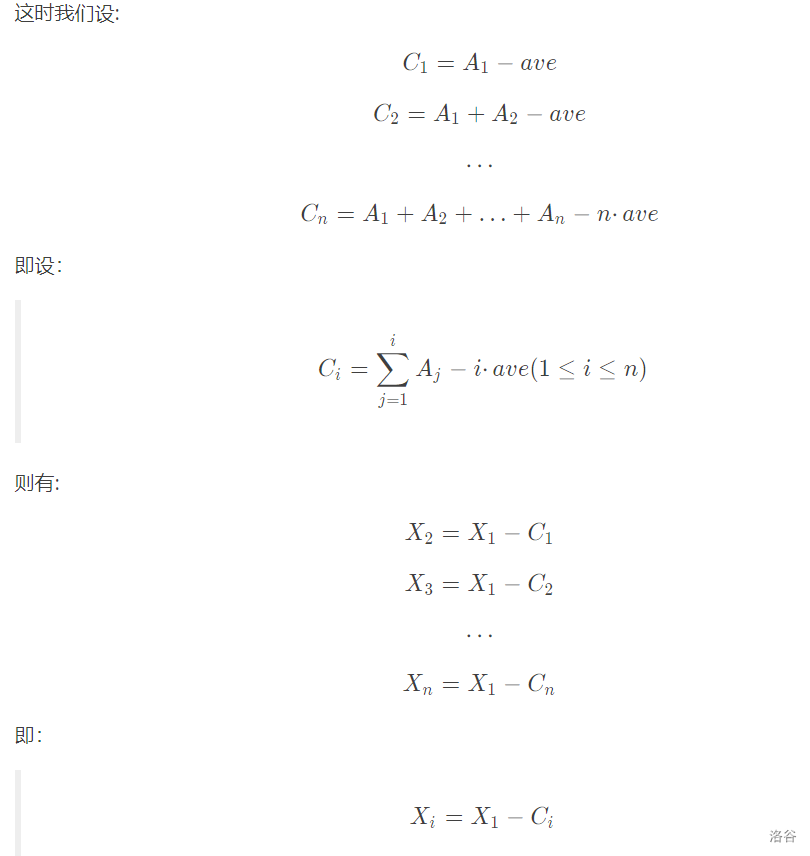

根据初中知识 很明显这个点就是中位数
点击查看代码
#include<bits/stdc++.h>
#define max(a,b) a>b?a:b
#define min(a,b) a<b?a:b
#define inline il
typedef long long ll;
typedef long double ld;
const int inf = 0x7fffffff;
const int N = 1e6+1;
ll n;
ll a[N],c[N];
ll ave,ans,mid;
using namespace std;
int main()
{
scanf("%lld",&n);
for(int i=1;i<=n;++i)
scanf("%lld",&a[i]),ave+=a[i];
ave/=n;
for(int i=1;i<=n;++i)
c[i]=c[i-1]+ave-a[i-1];
sort(c+1,c+n+1);
mid=c[(n+1)/2];
for(int i=1;i<=n;++i)
ans+=abs(mid-c[i]);
printf("%lld",ans);
return 0;
}
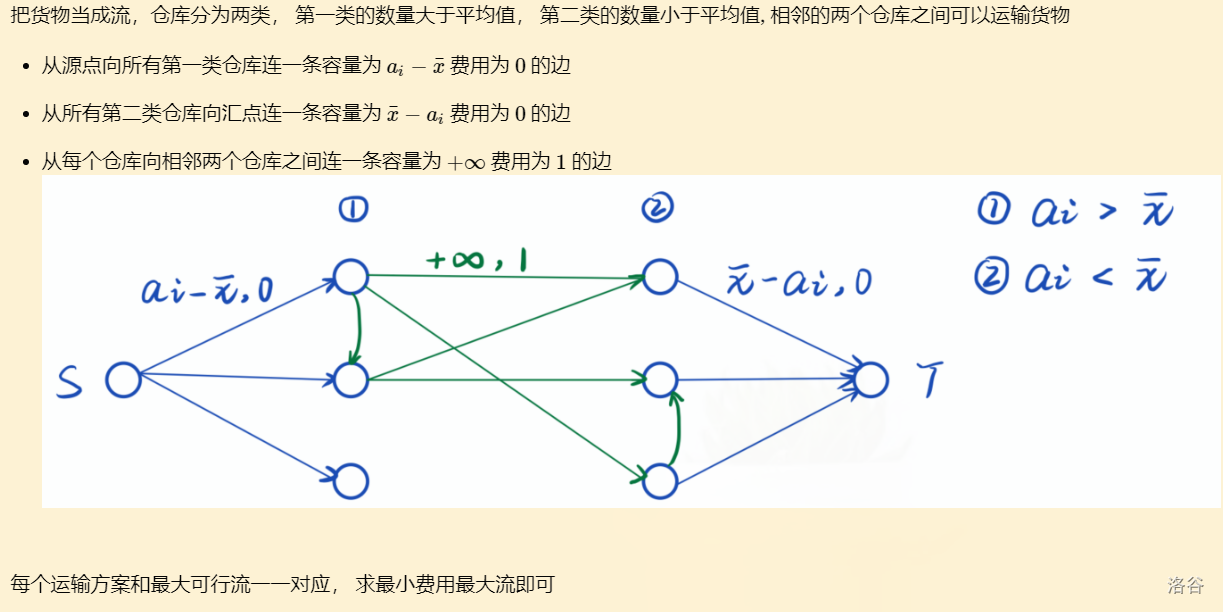
费用流做法:
P4016 负载平衡问题
这个题和糖果传递是一模一样的,学完网络流之后看到这个题目很典型的费用流
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
#define inf 1e9
const int maxn=105;
int head[maxn],cnt=1;
int pre[maxn],last[maxn],vis[maxn],d[maxn],ff[maxn],s[maxn];
int n,S,T,mincost;
struct bian{
int to,next,cost,flow;
}edg[maxn*maxn];
void add(int u,int v,int cost ,int flow){
edg[++cnt].next=head[u];head[u]=cnt;edg[cnt].flow=flow;edg[cnt].cost=cost;edg[cnt].to=v;
edg[++cnt].next=head[v];head[v]=cnt;edg[cnt].flow=0;edg[cnt].cost=-cost;edg[cnt].to=u;
}
queue<int>Q;
bool spfa(){
memset(vis,0,sizeof(vis));
memset(d,0x7f,sizeof(d));
memset(ff,0x7f,sizeof(ff));
d[S]=0;vis[S]=1;Q.push(S);pre[T]=-1;
while(!Q.empty()){
int u=Q.front();
Q.pop();vis[u]=0;
for(int i=head[u];i;i=edg[i].next){
int to=edg[i].to,flow=edg[i].flow,cost=edg[i].cost;
if(flow&&d[to]>d[u]+cost){
d[to]=d[u]+cost;
pre[to]=u;
last[to]=i;
ff[to]=min(ff[u],flow);
if(!vis[to]){
vis[to]=1;
Q.push(to);
}
}
}
}
return pre[T]!=-1;
}
void calc(){
while(spfa()){
int now=T;
mincost+=d[T]*ff[T];
while(now!=S){
edg[last[now]].flow-=ff[T];
edg[last[now]^1].flow+=ff[T];
now=pre[now];
}
}
}
int main(){
cin>>n;
S=0,T=n+1;
int tot =0;
for(int i = 1; i <= n; ++ i)
{
scanf("%d", &s[i]);
tot += s[i];
add(i, i < n ? i + 1 : 1, 1,inf);
add(i, i > 1 ? i - 1 : n, 1,inf);
}
tot /= n;
for(int i = 1; i <= n; ++ i)
if(s[i] > tot) add(S, i, 0,s[i] - tot);
else if(s[i] < tot) add(i, T,0,tot - s[i]);
calc();
cout<<mincost<<endl;
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号