L3-020 至多删三个字符

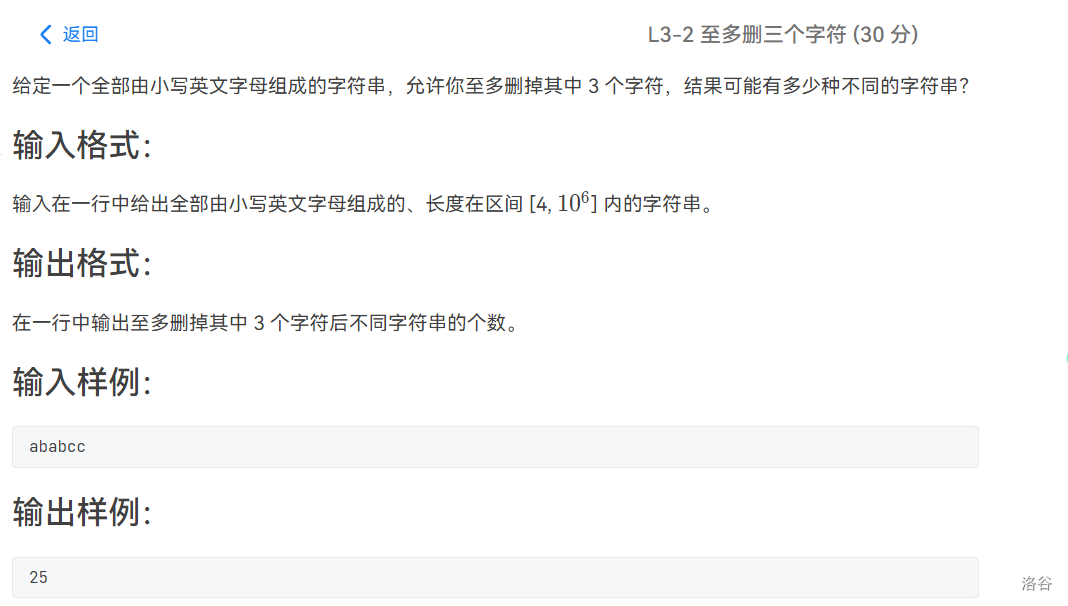
分析
一看就知道是个dp

很明显的转移方程：

dp[i][j]+=dp[i-1][j-1]+dp[i-1][j];

但是因为可能会有重复字符，导致两种不同的删除方法最后结果可能会是一样的

这个时候怎么办呢？

可以考虑转移方程再改一改条件，但是思来想去真的不好写

正面不好写那就反向写

考虑容斥，我们只要减掉重复的即可

因为重复的只可能出现在j的范围内

每次只要减掉最后与i相同的字符即可

因为我们这个是递推，前面的dp[][]已经是容斥过了，已经是答案了

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
void solve();
const int maxn=1e6+5;
string s;
ll dp[maxn][4];
int main(){
	int T;T=1;
	while(T--)solve();
     return 0;
}
void solve(){
	cin>>s;
	int len=s.size();
	for(int i=0;i<=len;i++)dp[i][0]=1;
	for(int i=1;i<=len;i++){
		int t=i-1;
		for(int j=1;j<=3&&i>=j;j++){
			dp[i][j]+=dp[i-1][j-1]+dp[i-1][j];
		if(j==1)
		if(t>=1&&s[t]==s[t-1])
		dp[i][j]-=dp[i-2][j-1];
		if(j==2){
		if(t>=1&&s[t]==s[t-1])
		dp[i][j]-=dp[i-2][j-1];
		else if(t>=2&&s[t]==s[t-2])
		dp[i][j]-=dp[i-3][j-2];
		}
		if(j==3){
			if(t>=1&&s[t]==s[t-1])
		dp[i][j]-=dp[i-2][j-1];
		else if(t>=2&&s[t]==s[t-2])
		dp[i][j]-=dp[i-3][j-2];
		else if(t>=3&&s[t]==s[t-3])
		dp[i][j]-=dp[i-4][j-3];
		}
		}
	}
	cout<<dp[len][3]+dp[len][0]+dp[len][1]+dp[len][2];
}