二叉树专题

之前学二叉树的时候不认真，昨天遇到打比赛遇到一个二叉树的板子题，没做出来，所以就想重新巩固一下
不过还好进我们学校的ACM的校队了

考虑什么情况下前后序都定下来的时候，但中序没定
前序：根节点+左子树＋右子树..........(1)
后序：左子树+右子树+根节点...........(2)
中序：左子树+根节点+右子树
规律有点点难找：
如果该节点只有一个儿砸，那么这个儿砸无论是在左边还是右边
都不会改变前后序的排布
但是中序相应的肯定就会变化了

问题转化为找到只有一个儿砸的结点就行了
根据(1)(2)发现
只要前序出现AB后序出现BA，那么A就是只有一个儿砸了

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
char s1[500],s2[500]; 
ll ans;
int main(){
	cin>>s1;cin>>s2;
	int len1=strlen(s1),len2=strlen(s2);
	for(int i=0;i<len1;i++)
	for(int j=1;j<len2;j++)
	if(s1[i]==s2[j]&&s1[i+1]==s2[j-1])
    ans++;
    cout<<(1<<ans)<<endl;
	return 0;
}

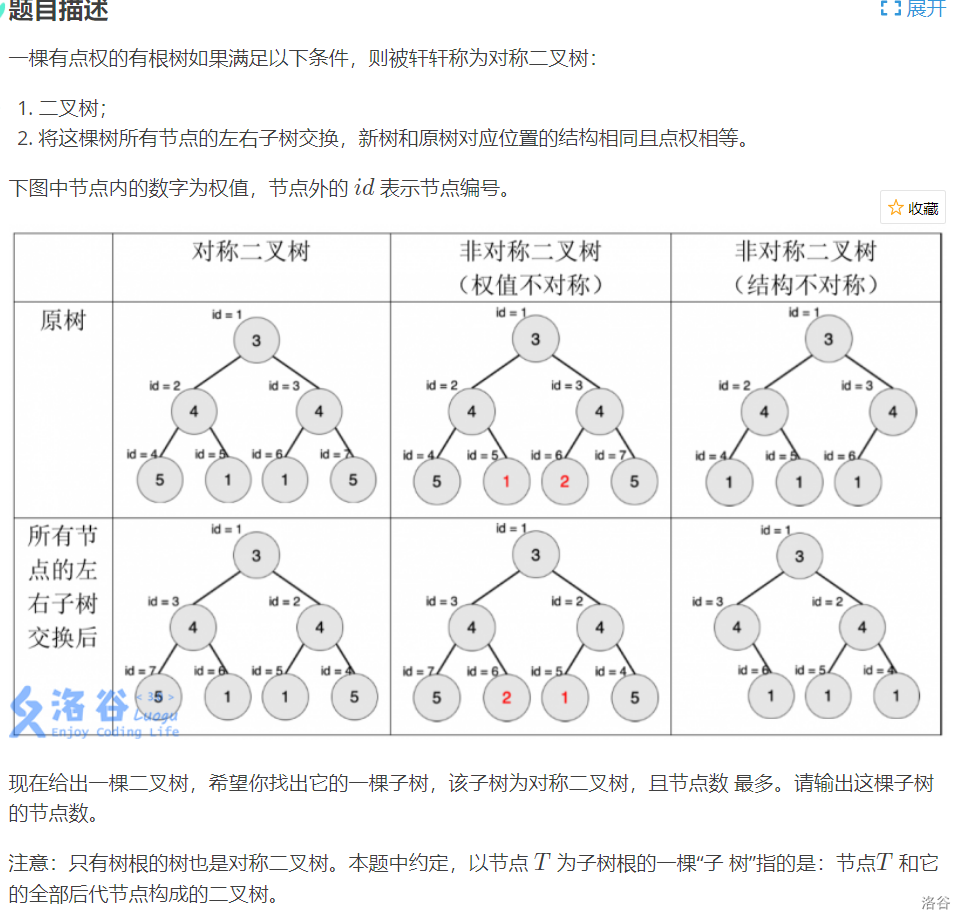
考虑直接递归判断，对每个结点进行判断，因为是二叉树，所以复杂度为nlogn

点击查看代码

#include<bits/stdc++.h>
using namespace std;
struct node{long long l,r,val;}bt[1000002];
bool same(long long now1,long long now2){//判断是否对称
	if(now1==-1&&now2==-1) return true;
	if(now2==-1||now1==-1) return false;//小技巧
	if(bt[now1].val!=bt[now2].val) return false;
	return same(bt[now1].l,bt[now2].r)&&same(bt[now1].r,bt[now2].l);//递归的判断左右子树相等
}
int count(long long now){//递归的对左右子树计数
	return now==-1?0:count(bt[now].l)+count(bt[now].r)+1;
}
int main(){
	int n,ans=0;cin>>n;
	for(int i=1;i<=n;i++) cin>>bt[i].val;
	for(int i=1;i<=n;i++) cin>>bt[i].l>>bt[i].r;
	for(int i=1;i<=n;i++)/*枚举每棵子树*/ if(same(i,i)) ans=max(ans,count(i));
	return 0&printf("%d",ans);
}

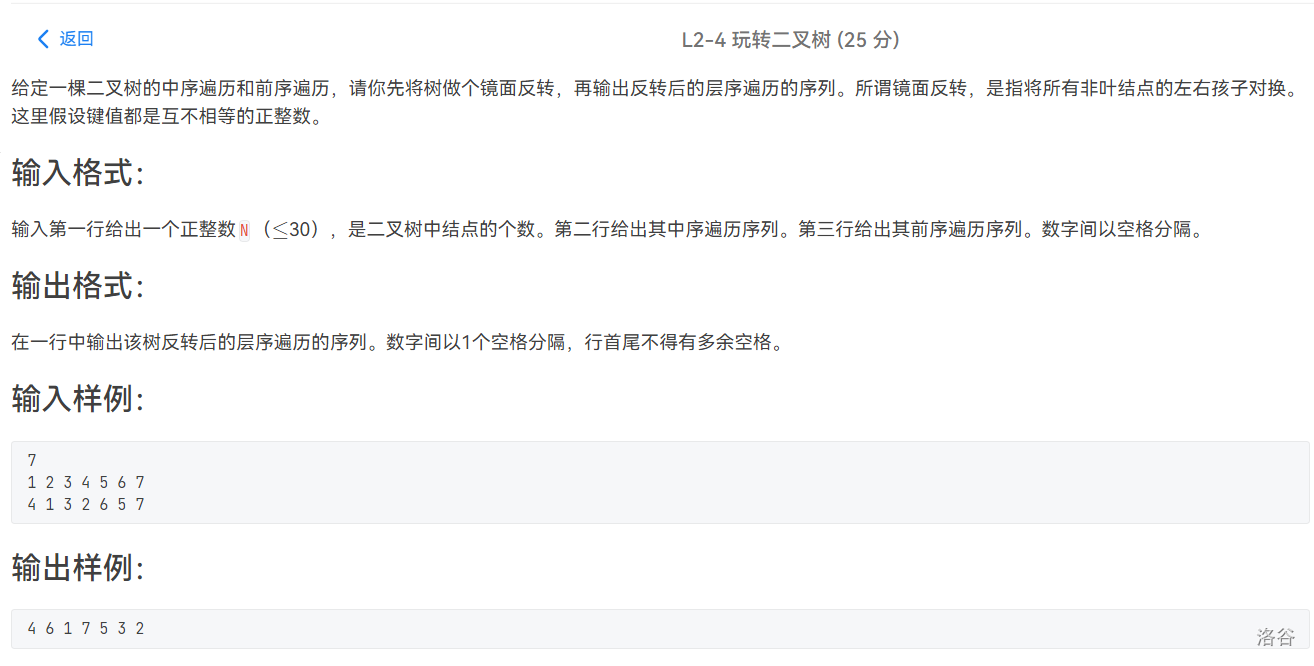
考试就是这道模板型的题目，把我考住了
就是一道模板题
唯一要注意的点就是：因为要镜面翻转，所以先遍历右子树就好了

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int mid[33];//zhong
int pre[33];//qian
int ans[125];
int n;
void dfs(int u,int midl,int midr,int k){
	if(midl>midr)return;
	int pos;
	for(int i=midl;i<=midr;i++){
		if(mid[i]==pre[u])
		pos=i;
	}
	ans[k]=pre[u];
	dfs(u+pos-midl+1,pos+1,midr,k*2);
	dfs(u+1,midl,pos-1,k*2+1);
}
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)scanf("%d",&mid[i]);
	for(int i=1;i<=n;i++)scanf("%d",&pre[i]);
	dfs(1,1,n,1);
	int cnt=0;
    for(int i=1;i<=124;i++){
    if(ans[i])
    cout<<ans[i],cnt++;
    if(cnt<n&&ans[i])cout<<" ";
	}
    
	return 0;
}

定义Count[i] 为以[1,i]能产生二叉搜索树的数目
则有count[i]=Σcount[1,k-1]count[K+1,i] (k<i)
明显count[k+1,i]=count[k+1-k,i-k]=count[1,i-k]
所以count[i]=Σcount[k-1]count[i-k] (k<i)
也就是卡特兰数的实现

比赛的时候读不懂题目就没做

其实就是 告诉后序排序 和中序排序

求之字形输出

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) x&(-x)
#define ll long long
int a[300005*4],b[300005*4],ans[300005*4];
int n; 
void dfs(int u,int k,int l,int r){
	int id;
	if(l>r)return;
	for(int i=l;i<=r;i++){
		if(a[i]==b[u]){
			id=i;break;
		}
	}
	ans[k]=b[u];
	int sumr=r-id+1;
	dfs(u-sumr,k<<1,l,id-1);
	dfs(u-1,k<<1|1,id+1,r);
} 
int fast_mi(int a,int b){
	int res=1;
	while(b){
		if(b&1)res*=a;
		a*=a;
		b>>=1;
	}
	return res;
}
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>a[i];//中序 
    for(int j=1;j<=n;j++)cin>>b[j];//后序 
    dfs(n,1,1,n);
    int tot=0;
    cout<<ans[1];
    for(int k=2;k<=20;k++){
    	if(tot>=n)return 0;
    	if(k%2){
    		int r=fast_mi(2,k)-1;
    		int len=fast_mi(2,k-1);
    		for(int i=r;i>=r-len+1;i--)
    		if(ans[i])cout<<" "<<ans[i],tot++;
    		if(tot>=n)return 0;
		}
		else {
			int l=fast_mi(2,k-1);
			int len=fast_mi(2,k-1);
			for(int i=l;i<=l+len-1;i++)
			if(ans[i])cout<<" "<<ans[i],tot++;
		    if(tot>=n)return 0;
		}
	}
	return 0;
}