Manacher——最快的找最长回文算法

Manacher

马拉车——Manacher算法解决的问题

给定一串字符串str，求str内的最长回文子串，我们可以从最朴素的算法开始，逐渐深入Manacher算法。

朴素穷举法

一直枚举字符串str的子串\((n^2个)\)，并判断子串是否为回文\([O(n)]\)。这个时间复杂度直接到\(O(n^3)\)了，一般题目都会超时。

中心扩散法

作为一个回文字符串，其必有一个回文中心，由中心向四周遍历，一次遍历两个方向。
以以下字符串为例:

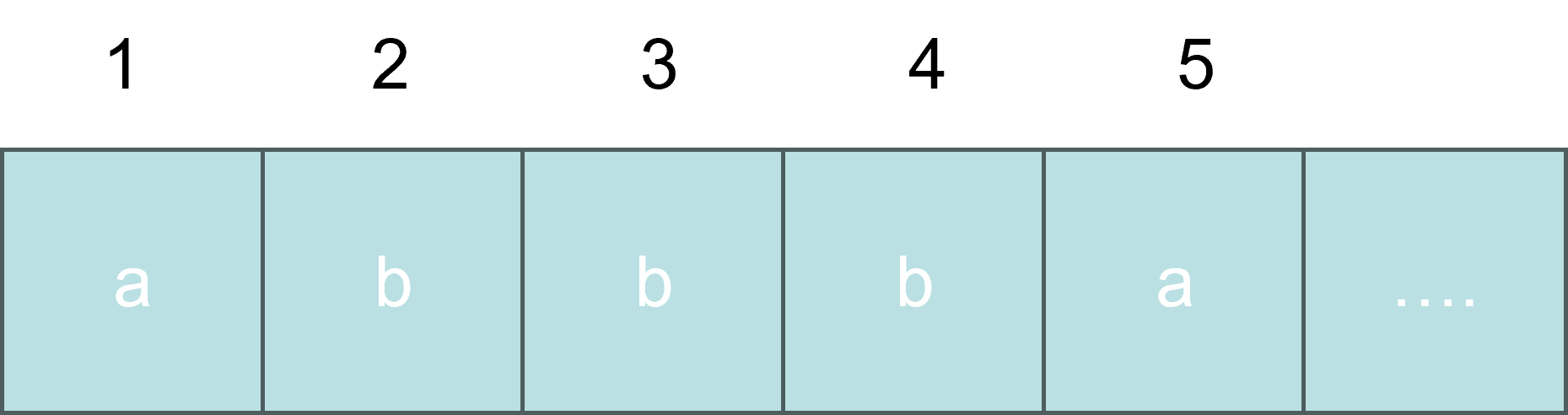
如果仅仅只是寻找子串，再判断回文的话，就是朴素的穷举法

点此查看字串

The sub-string of "abbba" without duplicate are <"a" "ab" "abb" "abbb" "abbba" "b" "bb" "bbb" "bbba" "bba" "ba">

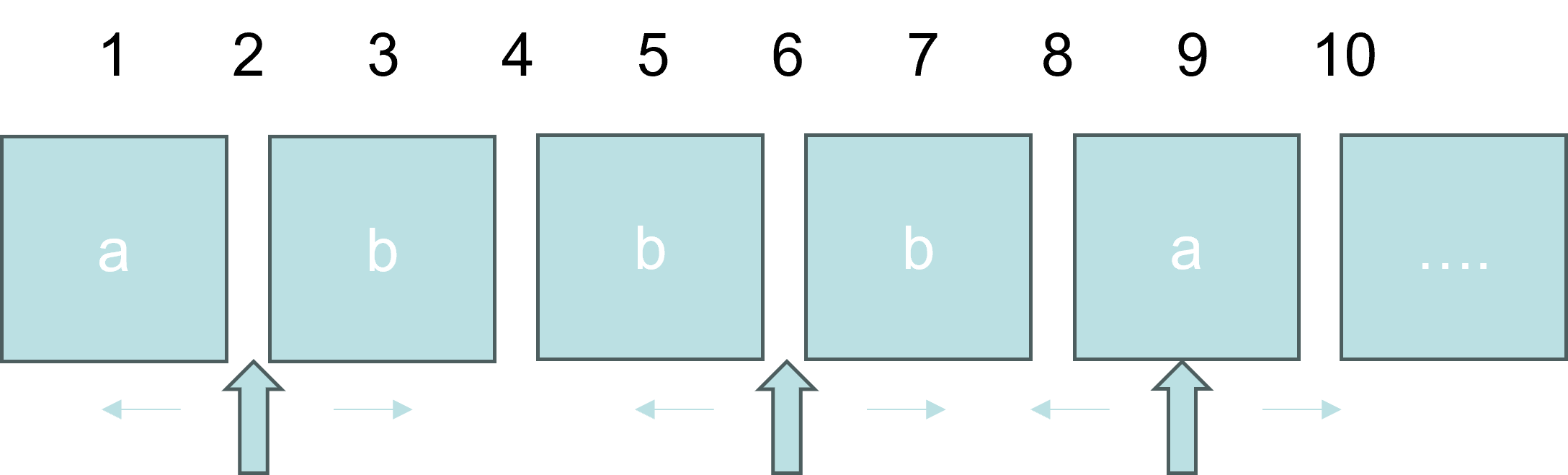再仔细思考一下，发现可以这样来寻找回文串 我们考虑将回文字符串分为两类，第一类是中心为字母的回文(如：aba)，第二类是不存在中心字母对称的回文(如：abba)，我们可以假想第二类是关于空白符对称的(ab ba)，将第二类转化为第一类问题来进行解决。 那我们就可以搜索每个可能的回文字符的中心，其中中心可能为：
1. 字符串中的每个字符（独立一个字符的字串也是以自身为中心的回文串）
2. 字符中间的空位(诸如序号1 $a$ 与序号3 $b$ 中间序号为2的空位)

之后以这些中心为起点向两边比较字符，直到失配（字符不一样）。

中心扩散的搜索效率

假定一个长为\(n\)的字符串，其可能的回文中心就有\(2n-1\)个，对每个中心实现由中间向两边的回文匹配。
相比朴素穷举法，中心扩散的方法将搜索范围从多达\(n^2\)种可能的字串降低到\(2n-1\)个中心。
因此，中心扩散的搜索效率可达\(O(n^2)\)。

Manacher

相比中心扩散法，马拉车运用动态规划的方法在中心扩散法的基础上进一步地减少了比较次数，是中心扩散法的优化。(用空间换了时间)这个算法利用了回文子串关于回文中心对称的特性。根据这个特性可以总结以下规律：

假定一个字符串是回文的，那么这个字符串除中心外中心的左半边和右半边是完全一样的子串。如"abbba"以\(str_3=b\)为中心那么中心的左半部分与右半部分完全一致。而我们搜索的顺序又是从左向右的，假定我们搜索过左半部分回文中心的最长回文串，那么右半部分的回文串就可以直接根据左半部分的结果来进行匹配操作。

Manacher的代码实现

void Manacher(char *T, int len)
{    // T[1…len]: #a#……#b#
	int center, right, radius;
	right = 0;
	for (int i = 1; i <= len; i++) {
		if (i >= right)
			radius = 1;
		else
			radius = min(right-i+1, Len[center*2-i]);
		while (T[i+radius] == T[i-radius])
			radius++;
		if (i + radius - 1 > right) {
			right = i + radius - 1;
			center = i;
		}
		Len[i] = radius;
	}
}