1.K-近邻算法的概述
K最近邻(k-Nearest Neighbor,KNN)分类算法,是一个理论上比较成熟的方法,也是最简单的机器学习算法之一。该方法的思路是:在特征空间中,如果一个样本附近的k个最近(即特征空间中最邻近)样本的大多数属于某一个类别,则该样本也属于这个类别。
2.自制数据集:
根据树的高度、落叶情况、树的叶类。这三个特征值作为判断标准来作样本集合,将样本数据存储在自己编撰的text.txt文本文件中,样本数量总共有30个,截图如下: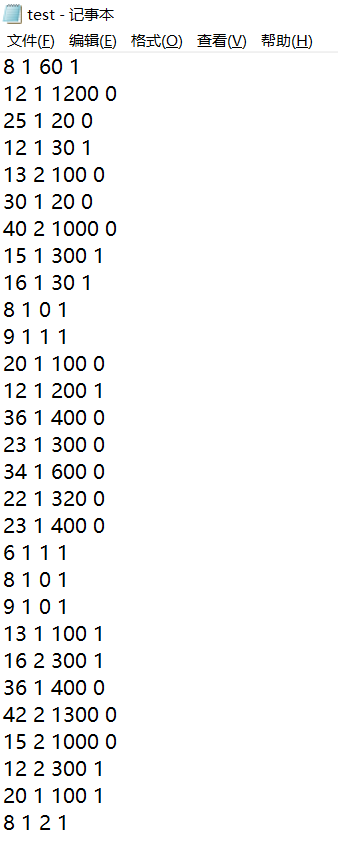
算法实现:
k-近邻算法:
点击查看代码
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize, 1)) - dataSet
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort()
classCount = {}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
点击查看代码
def file2matrix(filename):
fr = open(""C:/Users/wzj/Desktop/test.txt")
arrayOLines = fr.readlines()
numberOfLines = len(arrayOLines)
returnMat = zeros((numberOfLines,3))
classLabelVector = []
index = 0
for line in arrayOLines:
line = line.strip()
listFromLine = line.split('')
returnMat[index,:] = listFromLine[0:3]
classLabelVector.append(int(listFromLine[-1]))
index+=1
return returnMat,classLabelVector
点击查看代码
import matplotlib
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x=returnMat[:,0]
y=returnMat[:,1]
z=returnMat[:,2]
fig = plt.figure()
ax = Axes3D(fig)
ax.scatter(x,y,z,c=60.0*array(classLabelVector)+1,s=60.0)
plt.show()
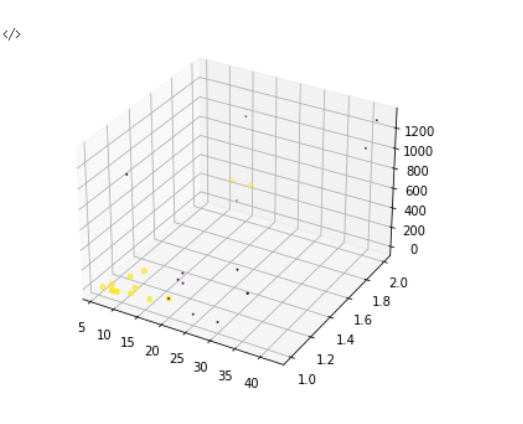
归一化特征值
点击查看代码
def autoNorm(dataSet):
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = np.zeros(np.shape(dataSet))
m = dataSet.shape[0]
normDataSet = dataSet - np.tile(minVals, (m, 1))
normDataSet = normDataSet/np.tile(ranges, (m, 1))
return normDataSet, ranges, minVals
点击查看代码
def datingClassTest():
hoRatio = 0.60
datingDataMat, datingLabels = file2matrix('D:/datingTestSet2.txt')
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normMat[i, :], normMat[numTestVecs:m, :], datingLabels[numTestVecs:m], 3)
print("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
if (classifierResult != datingLabels[i]): errorCount += 1.0
print("the total error rate is: %f" % (errorCount / float(numTestVecs)))
当K=1时
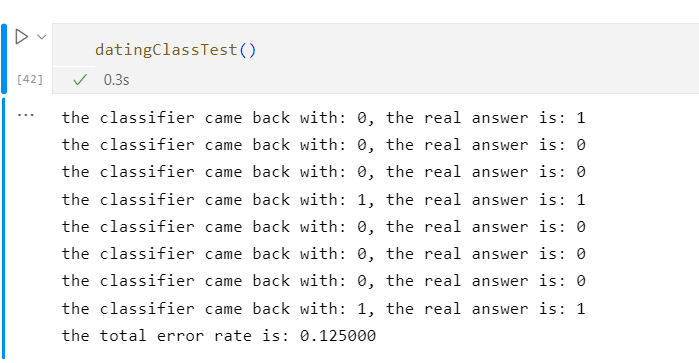
当K=2时
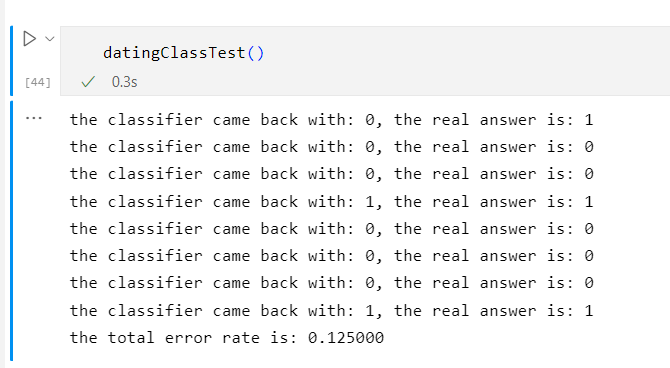
当K=3时
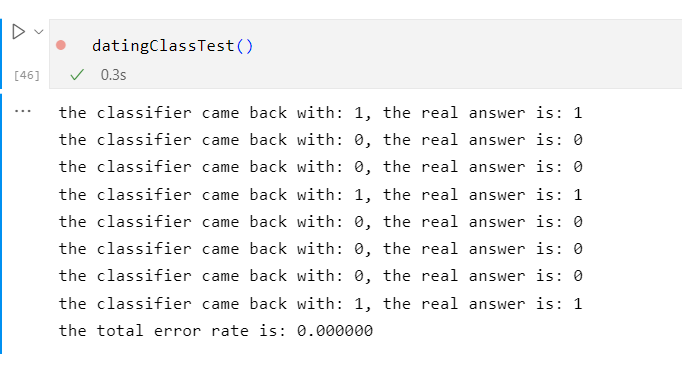
当K=4时
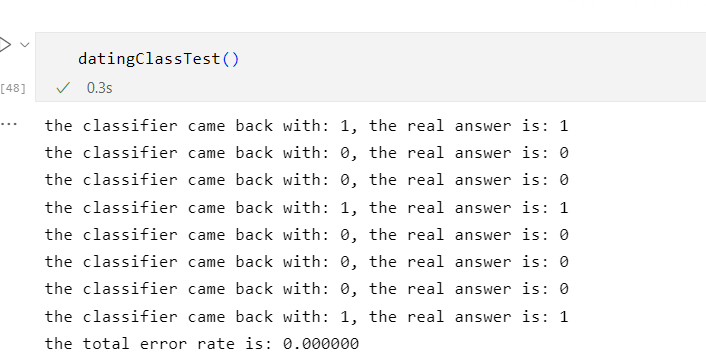
当K=5时
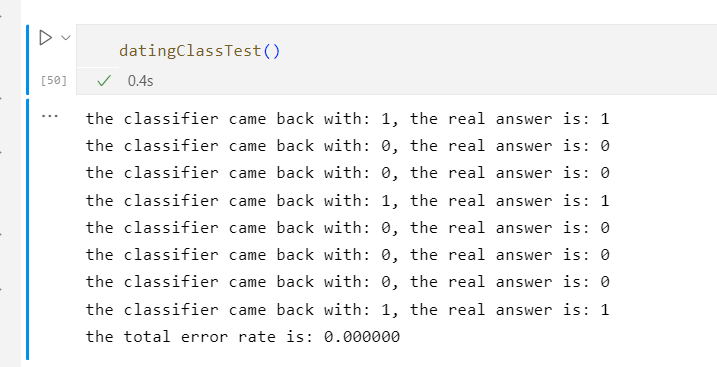
当K=6时
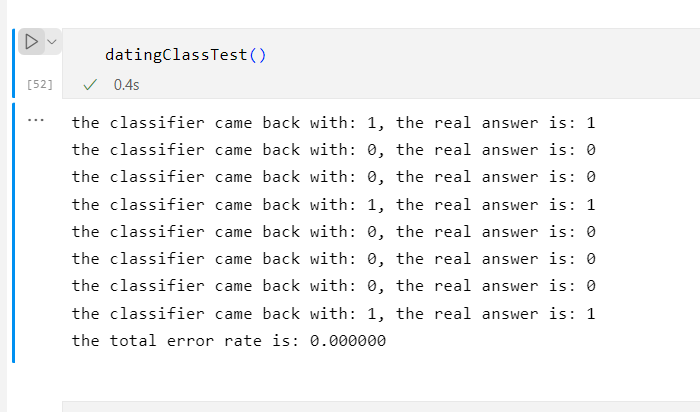
当K=7时
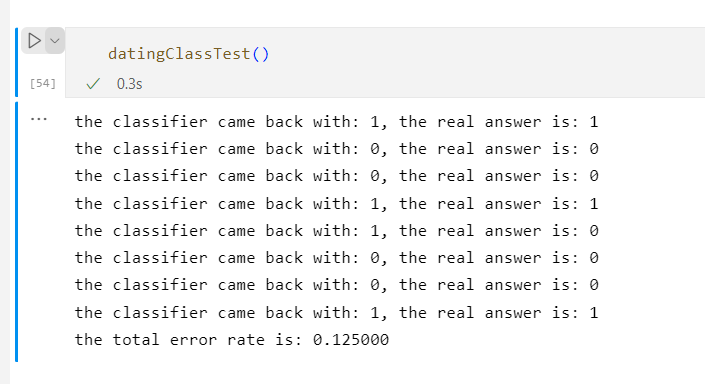
当K=8时
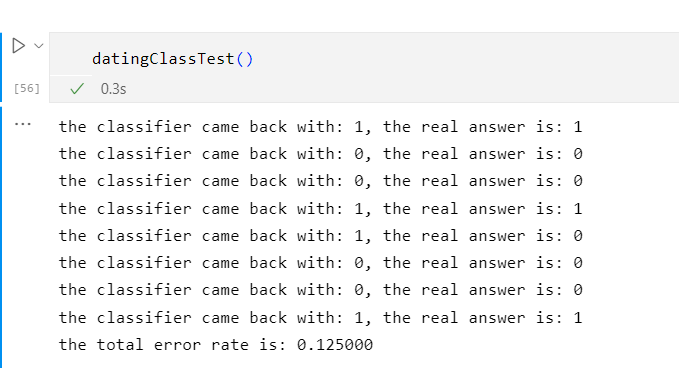
由此可见当K=3、4、5、6时,错误率最低
这是因为K值的大小不能取太小也不能取过大决定的



