二叉树的遍历

递归

前序遍历

定义一个   visited  函数来表示访问树中的某一个节点。visited 函数可以是任意的访问函数，只要满足输出的格式。如：

void visited(TreeNode* node)
{
    cout<<node->val<<endl;  
}

前序遍历的访问顺序为：先访问根节点，在访问左子树，在访问右子树

void Preorder(TreeNode* root)
{
    if(root==nullptr)
        return;
    visited(root);
    Preorder(root->left);
    Preorder(root->right);
}

中序遍历

中序的访问顺序为：先访问左子树，在访问根节点，最后访问右子树

void Inorder(TreeNode* root)
{
    if(root==nullptr)
        return;
    Inorder(root->left);
    visited(root);
    Inorder(root->right);
}

后序遍历

后序遍历的访问顺序为：先访问左子树，在访问右子树，最后访问根节点

void Postorder(TreeNode* root)
{
    if(root==nullptr)
        return;
    Postorder(root->left);
    Postorder(root->right);
    visited(root);
}

非递归迭代 O(n)

非递归形式一般使用栈来完成遍历过程，

前序遍历

主要思想：

（1）定义一个栈，首先将根节点压栈

（2）如果栈不为空，循环：

        （2.1）访问栈顶元素

        （2.2）如果栈顶元素的右孩子不为空，则将右孩子压栈

        （2.3）如果栈顶元素的左孩子不为空，则将左孩子压栈

Note：之所以先将右孩子压栈，再将左孩子压栈，是因为栈的先进后出原则。

void Preorder(TreeNode* root){
    if(root==nullptr)
        return;
    stack<TreeNode*> st;
    st.push(root);
    while(!st.empty())
    {
        root = st.pop();
        visit(root);
        if(root->right!=nullptr)
            st.push(root->right);
        if(root->left!=nullptr)
            st.push(root->left);
    }
}

中序遍历

中序遍历思想：

（1）首先将将根节点入栈，然后访问其左孩子，将其左孩子的左孩子依次入栈，

（2）然后访问栈顶元素，栈顶元素出栈，

        （2.1）如果栈顶元素有右孩子，则将右孩子入栈

循环（1）（2），直到全部遍历一遍。

void Preorder(TreeNode* root){
    if(root==nullptr)
        return;
    stack<TreeNode*> st;
    while(!st.empty()||root!=nullptr)//栈不为空，或者树中元素没有遍历完
    {
        while(root!=null) //如果当前节点不为空，当前节点入栈，访问左子树
        {
            st.push(root);
            root= root->left;
        }
        if(!st.empty())//栈不为空，此时栈顶元素是最左下孩子节点，访问此节点，栈顶元素弹出，指向元栈顶元素的右子树
        {
            root = st.top();
            visit(root);
            st.pop();
            root = root->right;
        }
    }
}

后序遍历

后序遍历相对比较麻烦，因为根节点是最后访问的，因此需要记录根节点是第几次被扫描。因此定义一个新的结构体，表示新的节点结构

struct StackNode{
    TreeNode* r;
    bool isFirst;//表示当前节点是否是第一次被访问
};

后序遍历的基本思想：

（1）首先依然是将当前节点及其左子树的左节点...入栈，

（2）如果栈不为空：

      （2.1） 弹出栈顶元素

      （2.2） 如果此元素是第一次被访问（弹出）：  则将其弹出次数加1（表示成不是第一次弹出），将其再次入栈

                   否则：直接访问此元素，然后将当前节点置为空，防止再次循环将左子树入栈。

循环上述（1）（2）最终访问所有的元素。

void Postorder(TreeNode* root){
    if(root==nullptr)
        return;
    stack<StackNode> st;
    StackNode snode;
    while(!st.empty()||root!=nullptr)//栈不为空，或者树中元素没有遍历完
    {
        while(root!=null) //与前序遍历类似，将所有的从根节点开始到左孩子节点入栈
        {
            snode.isFirst = true;
            snode.r = root;
            st.push(snode);
            root= root->left;
        }
        if(!st.empty())//栈不为空
        {
           snode = st.top(); //弹出栈顶元素
           s.pop();
           if(snode.isFirst) //如果弹出的栈顶元素是第一次被扫描，（刚入栈）
           {
               snode.isFirst = false; //则将扫描次数加1
               s.push(snode); //再将此节点入栈，然后扫描右子节点
               root = snode.r->right;
           }
           else
           {
               visit(snode); //如果不是第一次被扫描，则直接访问该元素，并将root 赋值为空，防止再次将左孩子入栈。
               root = nullptr;
           }
        }
    }
}

Morris Traversal

Morris Traversal只需要O(1)空间，而且同样可以在O(n)时间内完成。

要使用O(1)空间进行遍历，最大的难点在于，遍历到子节点的时候怎样重新返回到父节点（假设节点中没有指向父节点的p指针），由于不能用栈作为辅助空间。为了解决这个问题，Morris方法用到了线索二叉树（threaded binary tree）的概念。在Morris方法中不需要为每个节点额外分配指针指向其前驱（predecessor）和后继节点（successor），只需要利用叶子节点中的左右空指针指向某种顺序遍历下的前驱节点或后继节点就可以了。

前序遍历

1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。
2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。
    a) 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。输出当前节点（在这里输出，这是与中序遍历唯一一点不同）。当前节点更新为当前节点的左孩子。
    b) 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空。当前节点更新为当前节点的右孩子。
3. 重复以上1、2直到当前节点为空。

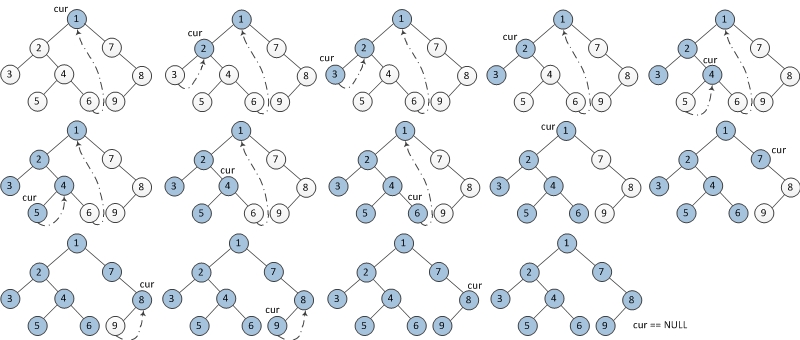
void morrisPreorder(TreeNode* root)
{
    TreeNode* cur=root, *prev = nullptr; //prev 用来表示中序遍历下的前驱
    while(cur!=nullptr) //循环的条件，cur不为空
    {
        if(cur->left ==nullptr) //如果左子树为空，则直接访问当前节点，转向右子树
        {
            visited(cur);
            cur = cur->right;
        }
        else  //如果左子树不为空，则寻找左子树中的中序遍历的最后一个节点，作为当前节点的前驱节点
        {
            prev = cur->left; 
            while(prev->right!=nullptr && prev->right!=cur)
                prev = prev->right;
               
            if(prev->right == nullptr) //如果最右节点的右子树为空，则线索化为当前节点，并访问当前节点
            {
                visited(cur);
                prev->right = cur;
                cur = cur->left;
            }
            else{
                prev->right = nullptr; //如果已经线索化，则说明包括当前节点在内的所有节点都已经被访问过，则访问当前节点的右子树
                cur = cur->right;
            }
        }
    }    
}

中序遍历

1. 如果当前节点的左孩子为空，则输出当前节点并将其右孩子作为当前节点。

2. 如果当前节点的左孩子不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

   a) 如果前驱节点的右孩子为空，将它的右孩子设置为当前节点。当前节点更新为当前节点的左孩子。

   b) 如果前驱节点的右孩子为当前节点，将它的右孩子重新设为空（恢复树的形状）。输出当前节点。当前节点更新为当前节点的右孩子。

3. 重复以上1、2直到当前节点为空。

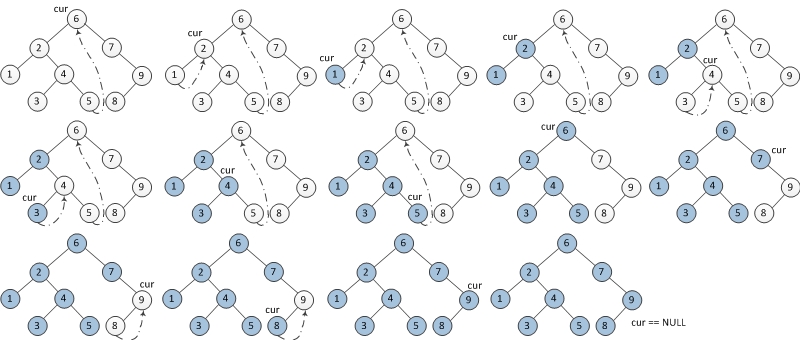
void morrisInorder(TreeNode* root){
    TreeNode* cur = root, *prev = nullptr;
    while(cur!=nullptr) 
    {
        if(cur->left==nullptr){//左孩子为空
            visit(cur);
            cur = cur->right;
        }
        else{ //左孩子不为空，找到前驱节点
            prev = cur->left;
            while(prev->right!=nullptr)
                prev = prev->right;
            if(prev->right == nullptr){ //前驱节点的右孩子为空，将其线索化到当前节点
                prev->right = cur; 
                cur = cur->left;
            }
            else{//右孩子已经线索化，访问当前节点，恢复右孩子节点，当前节点指向其右孩子
                prev->right = nullptr;
                visit(cur);
                cur =cur->right;
            }
        }
    }
}

后序遍历

后续遍历稍显复杂，需要建立一个临时节点dump，令其左孩子是root。并且还需要一个子过程，就是倒序输出某两个节点之间路径上的各个节点。

步骤：

当前节点设置为临时节点 dump

1. 如果当前节点的左孩子为空，则将其右孩子作为当前节点。

2. 如果当前节点的左孩子不为空，则在当前节点的左子树中找到当前节点在中序遍历下的前驱节点。

     a) 如果前驱节点的右孩子为空，将其右孩子设置为当前节点。当前节点更新为当前节点的左孩子。

     b) 如果前驱节点的右孩子为当前节点，将它的右孩子重新设置为空。倒序输出从当前节点的左孩子到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右孩子。

3. 重复以上1,2直到当前节点为空。

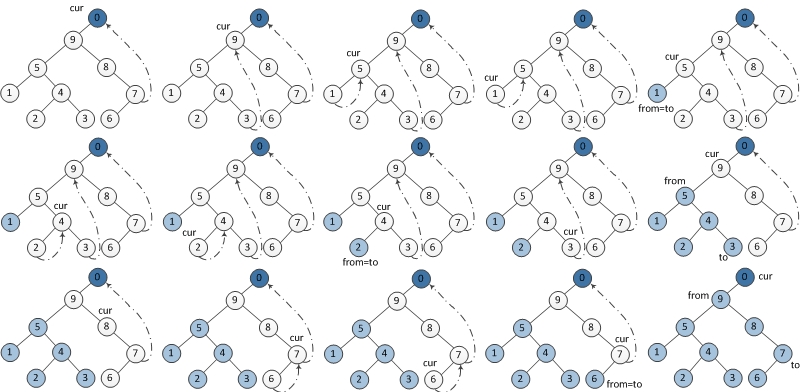
void reverse(TreeNode *from,TreeNode *to)
{
    if(from==to)
        return;
    TreeNode *x = from, *y = from->right, *z;
    while(true)
    {
        z = y->right;
        y->right = x;
        x = y;
        y = z;
        if(x==to)
            break;
    }
}
void visit(TreeNode* from,TreeNode* to)
{
    reverse(from,to);//逆转
    TreeNode *p = to;
    while(true)
    {
        visit(p);
        if(p==from)
            break;
        p->p->right;
    }
    reverse(to,from);//恢复
}

void morrisPostorder(TreeNode* root){
    TreeNode dump(0);
    dump.left = root;
    TreeNode* cur = &dump, *prev = nullptr;
    while(cur!=nullptr) 
    {
        if(cur->left==nullptr){
            cur = cur->right;
        }
        else{ 
            prev = cur->left;
            while(prev->right!=nullptr && prev->right!=cur)
                prev = prev->right;
            if(prev->right == nullptr){ 
                prev->right = cur; 
                cur = cur->left;
            }
            else{
                
                visit(cur->left,prev);
                prev->right = nullptr;
                cur =cur->right;
            }
        }
    }
}