7-1 二分查找
输入n值(1<=n<=1000)、n个非降序排列的整数以及要查找的数x,使用二分查找算法查找x,输出x所在的下标(0~n-1)及比较次数。若x不存在,输出-1和比较次数。

1 int BinarySearch(int a[], int x, int n) 2 { 3 int count = 0; 4 int left = 0; 5 int right = n-1; 6 while(left<=right) 7 { 8 int middle = (left+right)/2; 9 if(x==a[middle]) 10 { 11 count++; 12 cout << middle << endl; 13 cout << count; 14 return 0; 15 } 16 if(x>a[middle]) left = middle + 1; 17 else right = middle - 1; 18 count++; 19 } 20 cout << "-1" << endl; 21 cout << count; 22 return 0; 23 }
这个代码是在书中“二分搜索技术”的代码的基础上修改而来的,主要添加了一个新的变量count储存比较次数,将原本搜索到数据后的返回值改为对count加1,并输出middle数据及count数据。同时,将原本最后在未能搜索到数据时返回-1改为输出-1及count数据并结束binary search。
算法时间复杂度及空间复杂度分析:
以最坏情况考虑,将搜索n/2^m次,所以m=logn,及O(logn)。
空间复杂度应为一个常数,所以为O(1).
心得体会:对于这个二分查找的题目,本身并不难,但是在过程中,我们仍犯了一些不该犯的错误,如对于count变量的处理思路不清晰,没有想到在对middle输出(即在数组中查找到数据后)前应加入对count最后一次搜索的count计算,导致一直不能输出正确数据,最后仍旧是老师提醒后,才明白,说明我们对于这个编程思路不够清晰,没有考虑周全。
7-2 改写二分搜索算法
设a[0:n-1]是已排好序的数组,请改写二分搜索算法,使得当x不在数组中时,返回小于x的最大元素位置i和大于x的最小元素位置j。当搜索元素在数组中时,i和j相同,均为x在数组中的位置。

1 int BinarySearch(int a[], int x, int n) 2 { 3 int left = 0; 4 int right = n-1; 5 int i=0, j=0; 6 while(left<=right) 7 { 8 int middle = (left+right)/2; 9 if(x==a[middle]) 10 { 11 cout << middle << " " << middle; 12 return middle; 13 } 14 if(x>a[middle]) left = middle + 1; 15 else right = middle - 1; 16 } 17 if(left>right) 18 { 19 i = left-1; 20 j = left; 21 } 22 cout << i << " " << j; 23 return -1; 24 } 25 26 int main() 27 { 28 int n; 29 int x; 30 cin >> n >> x; 31 int a[n]; 32 for(int i=0; i<n; i++) 33 { 34 cin >> a[i]; 35 } 36 if(x<a[0]) 37 { 38 cout << "-1 0"; 39 return 0; 40 } 41 else if(x>a[n-1]) 42 { 43 cout << n-1 << " " << n; 44 return 0; 45 } 46 BinarySearch(a,x,n); 47 return 0; 48 }
这个代码依旧是在“二分搜索技术”代码的基础上修改而成的。首先,因为数组为已排好序的数组,所以对于x比数组最大值大和比最小值小的情况,题目以明确给出“若x小于全部数值,则输出:-1 0 若x大于全部数值,则输出:n-1的值 n的值”的要求。因此,我们在main函数中加入判断语句,判断x是否在数组中,并对两种情况给出相应输出并直接结束。在判断x位于数组中后,进入binarysearch函数进行搜索。同样,我们在开头加入两个新变量i和j来保存小于x的最大元素的最大下标i和大于x的最小元素的最小下标j。然后,在已查找到x的返回值middle之前,加入对middle的两次输出,以满足题目要求的i和j的输出。另外,在所有判断完成后。可以断定只有当left指向比right大的时候,才会跳出while循环。此时x不在数组中,数组中比x大的数为left所指向的数,比x小的数为right所指向的数,因此,对i赋值left-1(left-1在此时与right所指向相同),j赋值left,并输出i和j。
算法时间复杂度及空间复杂度分析:
以最坏情况考虑,将搜索n/2^m次,所以m=logn,及O(logn)。
空间复杂度应为一个常数,所以为O(1).
心得体会:
对于这个代码,个人感觉比较简单,主要是对于数组与x的先行判断,可以减少一定情况的时间成本。
7-3 两个有序序列的中位数
已知有两个等长的非降序序列S1, S2, 设计函数求S1与S2并集的中位数。有序序列A0,A1,⋯,AN−1的中位数指A(N−1)/2的值,即第⌊(N+1)/2⌋个数(A0为第1个数)。

1 #include <iostream> 2 using namespace std; 3 void Arrange(int s1[], int s2[], int N) 4 { 5 int X = N+N; 6 int s3[X]; 7 int i = 0, j = 0, k = 0; 8 while(i<N && j<N) 9 { 10 if(s1[i] < s2[j]) 11 { 12 s3[k] = s1[i]; 13 k++, i++; 14 } 15 else 16 { 17 s3[k] = s2[j]; 18 k++, j++; 19 } 20 } 21 while(i<N) 22 { 23 s3[k] = s1[i]; 24 k++, i++; 25 } 26 while(j<N) 27 { 28 s3[k] = s2[j]; 29 k++, j++; 30 } 31 cout << s3[(X-1)/2]; 32 } 33 34 int main() 35 { 36 int N; 37 cin >> N; 38 if(N>100000) 39 { 40 cout<<-1; 41 return 0; 42 } 43 int s1[N], s2[N]; 44 for(int i=0; i<N; i++) 45 { 46 cin >> s1[i]; 47 } 48 for(int i=0; i<N; i++) 49 { 50 cin >> s2[i]; 51 } 52 if( s1[(N-1)/2] == s2[(N-1)/2] ) 53 { 54 cout << s1[(N-1)/2]; 55 return 0; 56 } 57 Arrange(s1, s2, N); 58 return 0; 59 }
对于这个题目,因为两个数组为非降序序列的数组,而我们需要查找他们并集的中位数,所以首先可以进行一个判断,对S1和S2数组中位数是否相等进行判断(如果他们的中位数相等,因为他们为等长的数列,所以他们并集的数列的中位数必定仍为此数),如果相等就直接输出该数字,并直接结束,可以节省一些情况的时间成本。同时,我们在Arrange函数中定义一个新数组s3,其长度为原两个数组的总和。再定义i、j、k三个变量并置0作为s1、s2、s3判断过程中的指针。接着用while循环,在判断i和j指针均小于N的情况下一直判断s1[i]和s2[j]两个数据哪一个小,谁小就将谁存入s3数组中,同时将相应的指针后移(k++加上i++/j++)。再加上两个个新的while循环对i或者j小于N的情况将s1或s2数组中的剩余数据存入s3中。最后输出s3数组的中位数。
算法时间复杂度及空间复杂度分析:
Arrange中无好坏情况之分,都需要循环2N次,将s3数组填满,所以时间复杂度为O(n)。
空间复杂度为O(1),因为其中所使用的变量都为可计算的常数级。
心得体会:
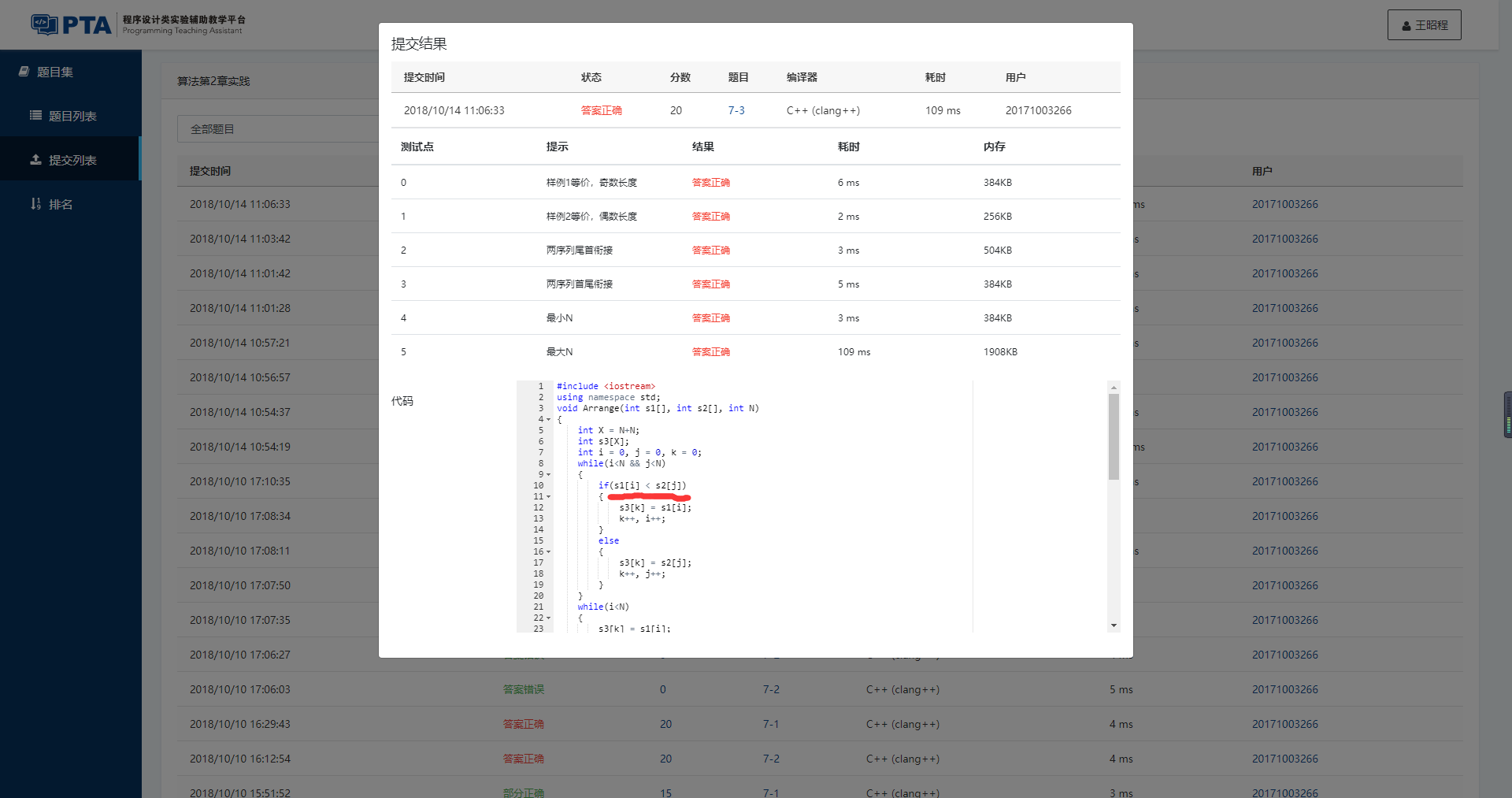
主要学习到的就是在写完代码后一定要检查。我们浪费了大量时间改写各个地方的条件判断,最后在一次重新看代码时,我才发现是i和j打错了造成的。原应该为“if(s1[i] < s2[j])”的判断语句,我们写成了“if(s1[i] < s2[i])”,再加上这个代码在pta中凑巧每次都能过5个中的3个,我们一直没有怀疑是代码写错,一直在为代码添加新的判断语句,或者修改原语句。而这个本应该可以耗费一点时间就检查出来的,我们却一直没有检查,浪费了许多时间。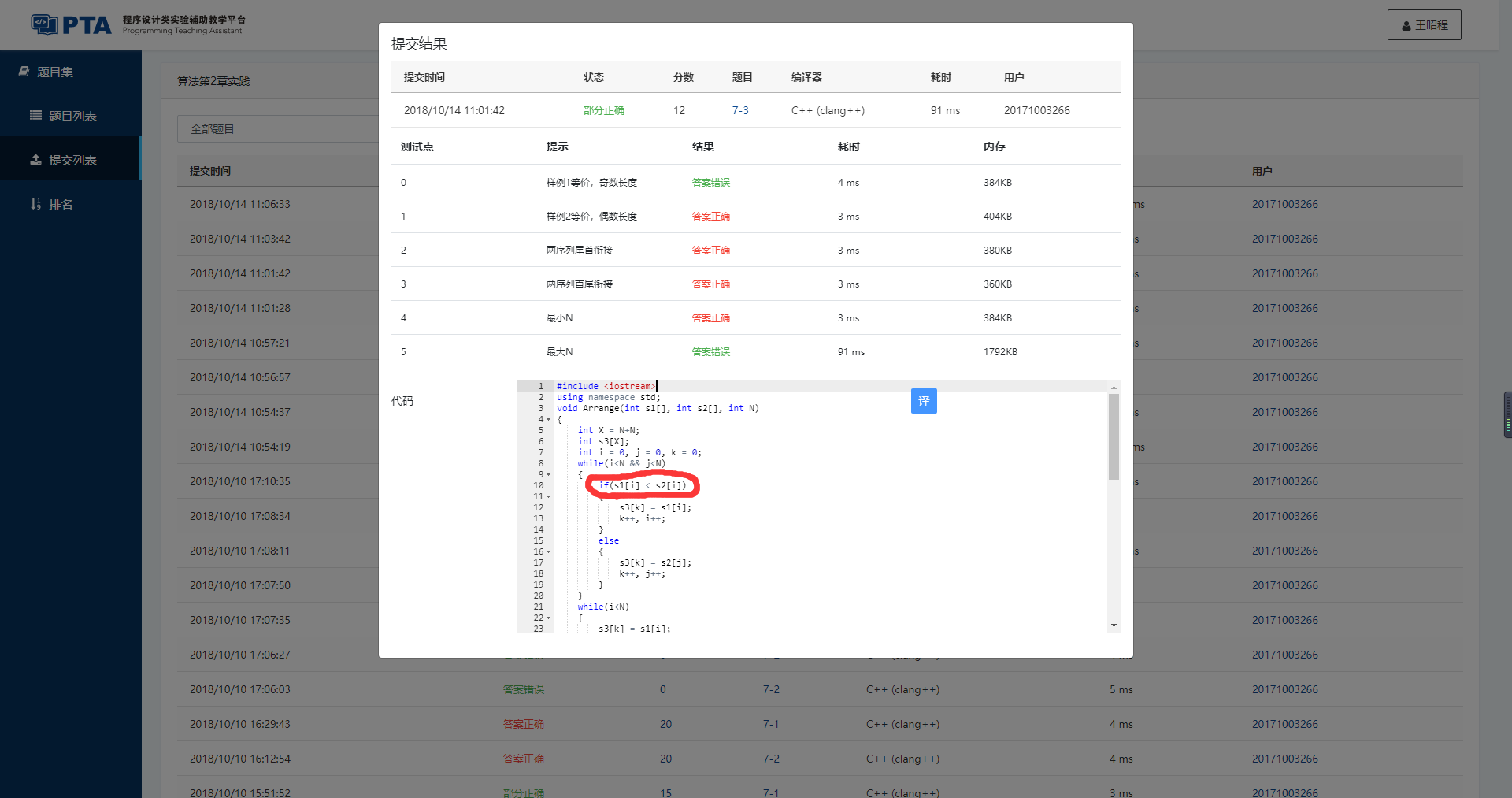




 浙公网安备 33010602011771号
浙公网安备 33010602011771号