组合数问题

从n个连续的数中选择m个互不相邻的数:

\[C_{n-m+1}^m \]

从n个连续的数组成的环中选择m个互不相邻的数:

\[C_{n-m}^m+C_{n-m+1}^{m-1}=\frac{n}{n-m}C_{n-m}^m \]

组合数问题：

\[C_n^m=n!/m!(n-m)! \]

从n个数中选择m个数，可以递推根据前面的数，可以递推出来后面的数。

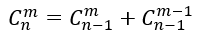
for (int i = 0; i <= 2000; i++)
		f[i][0] = 1;
for (int i = 1; i <= 2000; i++)
{
	for (int j = 1; j <= i; j++)
	{
		f[i][j] = (f[i - 1][j - 1] + f[i - 1][j]) % k;
	}
}

错排

1~n的n个数的全排列，其中错排的情况有多少组。

（错排：对于所有的数1<=x<=n，x的位置不在第x个）

即 ：某人写了 n封信和 有n 个信封，如果所有的信都装错了信封。

\(f(i)\)表示i个数有多少组错排

f[1]=0; f[2]=1; f[3]=2;

对于所有(i>=3) \(f[n]=(f[n-1]+f[n-2])*(n-1)\)

公式解释：

假设得到了f[1],f[2],......f[n-1] ,要求f[n].

第n个数放在第n个，依次和前面的n - 1个错排的数互换位置 ，总共有（n-1）*f[n-1].

从n-1个数中挑一个数i，有n-1种情况，i放在第i个数哪里，其余n-2个数错排，将i放在第n个数，n放在i哪里，总共（n-1）*f[n-2]

综上：

f[1]=0; f[2]=1;

\(f[n]=(f[n-1]+f[n-2])*(n-1)\) (i>=3)

数学期望

有n个物品，每个物品被挑选的概率为x，求数学期望：

\(n\times C_n^0 x^n+(n-1)\times C_n^1 x^(n-1)\times (1-x)+(n-2)\times C_n^2 x^(n-2)\times (1-x)^2+(n-3)\times C_n^3 x^(n-3)\times (1-x)^3+......+1\times C_n^n (1-x)^n\)

上式等于\(x\times n\)

组合数例题

CSP-S2019] Emiya 家今天的饭 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)*

点击查看代码