AtCoder 做题简记
以前做过的题目就懒得更在里面了
AGC 做题简记
AGC001
ABCDE 略
AGC001F Wide Swap
过于神仙,完全没思路
发现限制比较神必,但是发现我们给排列求个逆 $Q=P^{-1}$ ,那么限制就变为了若 $|q_i-q_{i+1}| \ge K$ ,就可以交换 $q_i,q_{i+1}$ ,我们要最小化的目标变成了要让 $q_i=1$ 的 $i$ 尽量小,在此基础上 $q_j=2$ 的 $j$ 也要尽量小,很熟悉?
我们思考是如何建边的,可以发现如果 $|q_i-q_j| < K$ ,那么 $q_i,q_j$ 的相对顺序就不能改变了,回到原排列上就是 $|i-j|<K$ 是 $p_i$ 和 $p_j$ 的相对大小永远不变,所以我们可以利用 $P$ 建边,对于 $|i-j|<K$ ,如果 $p_i<p_j$ 就 $i \leftarrow j$ ,否则就 $j \rightarrow i$
但是注意我们连边是借助 $P$ ,但这个建出的 $DAG$ 是要求转化为 $Q$ 的答案,所以建反图每次取最大拓扑即可,找入度为 $0$ 的点就是维护区间 $\max$ ,倘若除开已经被删掉的点满足 $\max\limits_{i-K+1 \le j \le i+K-1} p_j=p_i$ 那么就说明入度为 $0$ 了,加到堆里即可,时间复杂度 $O(n \log n)$
UPD. 还有一种归并做法,直接贴链接了
AGC002
ABC 略
AGC002D Stamp Rally
可以直接二分 + $Kruskal$ 重构树,也可以整体二分 + 可撤销并查集,时间复杂度 $O(n \log^2 n)$ , $O(n \log n)$ 的做法大概就是整体二分的时候每层从左往右扫加边即可
AGC002E Candy Piles
博弈论是不是必做不出啊,还在那里想什么 $\text{SG}$ 函数,真的是逊毙了
考虑先从大到小排序,看作许多小球摆在那 (看我偷几张图来)
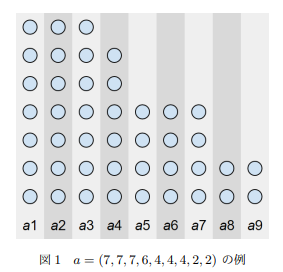
看成网格图可以发现题意可转化为从左下角的 $(0,0)$ 出发,可以往上往右走,走到边界算输:
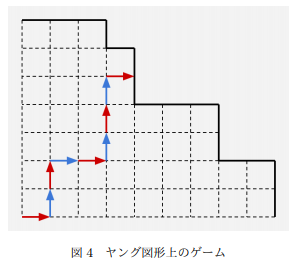
那么我们设边界点为先手必胜态(后文忽略先手),那么一个点为必输态当且仅当它右边和上面的点为必胜态,然后发现还是不会...
其实有个很巧妙的性质,那就是一条对角线上的点(当然是在碰到边界之前)胜负态是相同的!于是我们只需要找到最大的 $(i,i)$ 使得其没超过边界然后看看过两边胜负态即可
AGC002F Leftmost Ball
其实以前 $\text{y}\color{red}{\text{ybyyb}}$ 讲过...但是每次都不记得咋做了,只好自己推了!
显然 $K=1$ 答案为 $1$ ,下面只讨论 $K>1$ 的情况
转化一下题意,变成放 $n$ 个白球和 $n$ 种其他不同颜色的球各 $K-1$ 个,且第 $i$ 个白球前其他球的颜色个数不能超过 $i-1$ 个,那么就很好设状态了
设 $f_{i,j}$ 为已经放了 $i$ 个白球, $j$ 种其他颜色的球(可以放在第 $i$ 个白球后面),为了防止算重,我们钦定每次放白球都要放在当前第一个没放球的位置,放一种颜色的球时这种颜色的第一个也要放在当前第一个空位,就有转移
$$f_{i,j}=f_{i-1,j}+f_{i,j-1}(n-j+1)\tbinom{nK-i-(j-1)(K-1)}{K-2} \quad (j \le i)$$
直接转移即可,时间复杂度 $O(n^2)$
AGC003
ABC 略
AGC003D Anticube
发现如果我们能分解质因数就做完了,找到指数模 $3$ 后互补的数,取个数多的那边集合即可
所以我们直接 $\text{Pollard-Rho}$ 就切了!!!然而我并不会/ll
因为 $O(n\sqrt{V})$ 不行,那我们就退而求其次试试做 $O(nV^{\frac{1}{3}})$ ,也就是我们先分解出 $p \le V^{\frac{1}{3}}$ 的质因子
现在顶多剩下两个质因子了,如果除剩的数形如 $p,p^2 (p \le V^{\frac{1}{2}})$ ,那么直接把这个因子也算上即可,否则可以发现这个数必然跟任何一个数都凑不出完全立方数,不管直接加入答案, $map$ 维护一下即可
AGC003E Sequential operations on Sequence
以后要多想,不能一下就摆烂了/fn
显然如果 $q_i \ge q_{i+1}$ , $q_i$ 就是废的,先单调栈一下,记操作后的序列叫 $A,m=|A|$ ,然后?然后就不会摆烂了/ll
正着搞显然没前途,都不清楚到底长啥样,所以正难则反,我们考虑反着算出 $f_i$ 表示计算第 $i$ 次及以后的的操作整体基础值,发现每次余的一截都是差分可以解决的,重点看 $f_i$ 的贡献
首先有 $f_{i-1}$ 可以加上 $f_i \times \lfloor \frac{a_i}{a_{i-1}} \rfloor$ ,还多出来 $r=a_i \mod a_{i-1}$ 的,怎么办?发现这多出来的如果大于等于 $a_1$ ,那么必然又是前面一次操作后的序列的复制,我们找到最大的 $a_j \le r$ 的, $f_j$ 加上 $f_i \times \lfloor \frac{r}{a_{j}} \rfloor$ ,是一个递归过程,直接每次二分做即可
因为每次二分找到 $a_j \le r$ 都会使 $r$ 至少减半,所以复杂度为 $O(n \log^2 n)$
AGC003F Fraction of Fractal
$0$ 级分形是平凡的,只看 $K > 0$ 的分形
记 $c$ 为 $1$ 级分形的黑色点数,我们观察一下 $1$ 级分形对联通性的影响:
如果 $1$ 级分形上可以连下,左可以连右,那么答案必然是 $1$
如果 $1$ 级分形上不可以连下,左不可以连右,那么答案必然是 $c^{K-1}$
否则要么上可以连下,要么左可以连右,两者一样,假设是左可以连右进行计算
推一推发现答案可以写作 $K-1$ 级分形中黑点的个数 - 左右相邻两个都是黑格的对数
记 $a$ 为 $1$ 级分形中左右相邻两个都是黑格的对数, $b$ 为 $1$ 级分形中左边界与右边界都是黑色的行数,那么推一下能知道答案就是 $\begin{bmatrix}c & b \\0 & a \\\end{bmatrix}^{K-1}$ 的 $c'-b'$
AGC004
ABCD 略
AGC004E Salvage Robots
考虑机器人太多,动起来过于/tuu,我们可以将其视作出口和边界在动,一个显然的性质是肯定会扫成一个矩形,而且扫法比较工整,可以手玩一下
所以就设 $f_{u,d,l,r}$ 表示出口覆盖的矩形从出口的坐标开始上、下、左、右扩展了多大,前缀和一下就可以转移了
AGC004F Namori
注意到点为奇数必然无解(操作的奇偶性),然后肯定要分类讨论(良心的样例提示我们要分树,奇环,偶环讨论)
树肯定是最简单的,考虑树,因为是将相邻两个(也就是深度相差 \(1\) 的)且同色的翻转,有点诡异,考虑转化一下
因为树必然是二分图,转化为初始奇深度的点上都有一个棋子,每次可以将一个棋子移向相邻的一个空位,求都移到偶深度的点上的最小步数,显然奇深度点与偶深度点数不同就无解
考虑下界是什么,随便找一个点为根,令 \(sum_u\) 为 \(u\) 子树内深度为奇数的点的个数减去深度为偶数的点的个数,那么 \(u\) 与 \(fa_u\) 这条边至少要被经过 \(|sum_u|\) 次,显然也好构造至这个下界,所以答案就是 \(\sum\limits_{i=1}^n |sum_i|\) ,当然记得 \(sum_{rt} \not = 0\) 就无解
然后再来看看基环树的情况,显然环以外还是一样的,我们先任取一条边断开然后取其一端点作为根,然后来考虑这多出来的一条边的影响,由于上述是基于二分图考虑的,所以我们下面分作奇环和偶环来讨论
奇环
如果是奇环那么就是连接这染色二分图的同一颜色的点(也就是深度同奇偶的点),我们考虑对其操作是什么意义,相当于若两边同时是棋子(或空位),则可以把其变成都是空位(或棋子),也就是说其能(也只能)将在整棵树中多余的棋子或空位消掉偶数个
所以若 \(2 \not \mid sum_u\) ,则无解,否则我们必然会对这条边操作 \(\frac{sum_u}{2}\) ,也就是让环上的点的 \(sum\) 都减去 \(\frac{sum_u}{2}\) ,然后答案还是 \(\sum\limits_{i=1}^n |sum_i|\)
偶环
如果是偶环则仍然是二分图,那么这条边的作用也只能是移动棋子,我们设令 \(a_i\) 为只考虑环上对应编号 \(i\) 的点 \(u\) 的子树的 \(\sum_u\) ,设 \(x_i\) 为环上第 \(i\) 条边的移动次数(正负代表方向),那么需要满足
我们需要最小化 \(\sum\limits_{i=1}^{len}|x_i|\) (相当于环上边的移动总次数),所以改写一下,变形为
显然让 \(x_1\) 取 \(\{0,a_1,a_1+a_2,\ldots,\sum\limits_{i=1}^{len}a_i\}\) 的中位数即可
每种情况分别处理一下即可
AGC005
ABC 略
[AGC005D] ~K Perm Counting
错排问题直接上棋盘多项式,推荐这篇题解
[AGC005E] Sugigma: The Showdown
首先无限走就是当前 \(A\) 所在点在第一棵树有一条边 \((u,v)\) 使得在第二棵树上 \(dis(u,v) \ge 3\) ,这个显然
然后观察每个点是否能到,令 \(d_{1/2,u}\) 为 \(u\) 到第一/二棵树的起点的距离,每次只能走到 \(d_{1,u} < d_{2,u}\) 的位置,这样我们考虑先判能不能走到一个可以无限走的点,不能就走到 \(d_{2,u}\) 最大的点 \(x\) ,答案就是 \(2d_{2,x}\)
代码咕咕咕了
[AGC005F] Many Easy Problems
对于枚举的 \(i\) ,考虑一个点的贡献,发现方案数就是 \(i\) 个点不全选在一个子树内的方案的个数,记 \(size_{u,v}\) 为以 \(u\) 为根的时候 \(v\) 的子树大小,有
怎么卷积优化就不讲了,很多题解都讲了,代码也咕咕咕了
AGC006
ABE 略
[AGC006C] Rabbit Exercise
放在 C 题确实有点埋没了,感觉题目顺序应该是 ABECDF 或者 ABEDCF ?
考虑一次跳跃后 \(x_i'=x_{i-1}+x_{i+1}-x_{i}\) ,很经典,考虑差分,令 \(d_{i}=x_{i}-x{i+1}\) ,则一次跳跃为交换 \(d_{i-1},d_{i}\)
所以其实就是一轮就是一个置换,考虑找出每个置换环,每个环相当于转了 \(k \bmod len\) 位,时间复杂度 \(O(n)\) ,当然也可以直接写快速幂
[AGC006D] Median Pyramid Hard
经典题,中位数之类的一般考虑转成 \(01\) 做,所以考虑二分答案,转成 \(01\) 后就很好判断最顶上是 \(0\) 还是 \(1\) 了
[AGC006F] Median Pyramid Hard
这种题一般直接考虑 \((x,y)\) 代表 \(x\) 与 \(y\) 连边,这里我们显然连单向边
推一推可以发现,若是一个连通块能分层三染色(即若 \(x \rightarrow y\) ,则有 \(col_x=col_y+1 \bmod 3\) ),那么这个连通块要么不变(三种颜色没有全部出现,显然不会新增任何的边)或变成一张完全分层三染色图;若是不能分层三染色,可以发现整个连通块的边会连满,边数即为 \(size^2\)
AGC007
ABD 略
[AGC007C] Pushing Balls
这个时候的 C 怎么就这么难了/ll,完全做不出来/ll
先考虑 \(x=0\) 怎么做,也就是一开始每个间距都为 \(d\) 的情况,观察推了一个球以后的情况,首先会剩下 \(n-1\) 个球和 \(n\) 个坑,虽然有一段距离会变化,不满足原来的性质,但是根据期望的线性性,可以发现我们可以取期望距离直接当作距离!具体可能推一推能感受到,同时注意到每个剩下的段期望距离肯定相等,所以就是子问题了,那么我们只需要算一算推了 \(i\) 个球后的期望距离即可
先观察推一个球后的期望距离,首先有 \(\frac{1}{2n}\) 的概率将开头或者结尾一段删掉(为什么是 \(\frac{1}{2n}\) 是因为一共有 \(2n\) 段!),对于剩下的球和坑的期望距离没有影响,然后剩下的,对于第 \(i\) 段距离(这个 \(i\) 是重编号后的),都有 \(\frac{1}{2n}\) 的概率将它变长为 \(3 \cdot d\) ,所以
这样推完 \(i\) 次的 \(d\) 就能求了,然后考虑 \(x \ge 0\) 的情况,大胆猜测第一次直接把距离取平均然后当作 \(x=0\) 来做就是对的!为什么?其实考虑一种推球方案与和其对称的方案(第 \(t\) 个时刻 \(i\) 为左边推,则对称方案里第 \(t\) 个时刻 \(n-i+1\) 往右边推)两者加起来,就可以看作 \(x=0\) 的情况,而每一种方案都有其对称方案,所以就可以证明结论的正确性了
[AGC007E] Pushing Balls
考虑二分答案,注意到进去和出来没有本质区别,相当于是选两个点,满足这两个点是要经过当前子树根的返祖边(不一定存在),然后从其中一个点走到另一个点要满足将子树内走完且合法,钦定第一个点的深度小于第二个点
注意到若两种选法满足严格偏序,则有一种没有必要,所以双指针以后,设以 \(u\) 为根的子树的有用选法为 \(f_u\) ,则 \(f_u \le 2\min(f_{ls_{u}},f_{rs_{u}})\) ,则总选法最多为 \(T(n)=2T(n/2)+O(n)=O(n \log n)\) ,总复杂度为 \(O(n \log^2 n)\) ,当然偷懒写 \(\text{sort}\) 也是可以做的
[AGC007F] Shik and Copying String
首先肯定 \(T\) 串的每个位置 \(i\) 都是由 \(S\) 串小于等于 \(i\) 的一个位置贡献来的,这样我们就可以给每个位置 \(i\) 找一个匹配 \(p_i\) 满足 \(p_i \le i,S_{p_i}=T_i\) 且不能存在两个不同字符间的匹配有互相包含关系,因为这显然无法构造,在此前提下我们想要每个 \(j\) 尽量大,从后往前扫可以得到所有的匹配。注意到若 \(j<i,p_j=p_i\) ,则 \(j\) 的限制比 \(i\) 弱,不需要管 \(j\) 的限制了
现在就转化为了一些没有包含关系,且端点坐标互不相同的区间,每个左端点上都有一个向右移动的点,每 \(1\) 单位时间可以移动到一个位置,但要保证点的相对位置(坐标大小关系)不变,问所有点的最大移动次数最小是多少?
手玩一下可以发现,先把所有区间按左端点排序,一个点 \(i\) 的移动次数即为最大的 \(len\) 满足 \(r_i+len-1 \ge l_{i+len-1}\) ,双指针即可
AGC008
ABCD 略
[AGC008E] Next or Nextnext
考虑连有向边 \(a_i \rightarrow i\) ,则图的结构是基环外向树森林,首先分环和基环树(指有非环上点)的讨论
环
首先如果只有单独一个环,方案数也不只有一种,手玩一下可以发现除开一个点的奇数环都有两种方案,不过偶数环只有一种方案,因为如果偶数环 \(p_{p_i}=a_i\) 会断成两个环,接不起来,不合法
然后还有一种可能是两个长度相等的环可以合到一起(当然不能再合并了),方案数就为环长 \(len\)
不会算方案数可以看代码
基环树
注意到基环树肯定不能合并,只需要考虑单独的一个基环树怎么去计算,再推一下可以发现一定结构是环上每个点至多挂着一条链,且随便以环上一个点为根,每个深度(对环长取模)至多有一个环外点
然后因为 \(p_i=a_i\) 或 \(p_{p_i}=a_i\) ,所以一条链还可以把放在环上的位置(有点抽象,可以自己画张图)后移,但是如果后移前后面一个位置也放了个环外点则后面一条链也要后移,所以若放了环外点的连续段个数为 \(cnt\) ,方案数就为 \(2^{cnt}\)
不过注意特判环上面放满了点,则只有一种方案
时间复杂度 \(O(n)\)
[AGC008F] Black Radius
先考虑所有点都能选的情况,首先为了防止算重,我们考虑一种情况只在 \(d\) 最小的时候统计,注意只要没有覆盖整棵树,就不会出现存在两个最小的 \(d\) 的情况
记 \(f(u,d)\) 为将所有与 \(u\) 距离不超过 \(d\) 的节点都染成黑色的状态,可以发现会被计算的 \(d\) 肯定是段前缀,因为 \(d\) 越小越难被别的点表示出来
有一个显然的判定合法条件是不存在 \(u\) 的一个相邻的点 \(v\) 使得 \(f(u,d)=f(v,d-1)\) ,可以证明这是充要条件,这个条件又等价于除开以 \(v\) 为根的这棵子树,别的子树都会被 \(f(v,d-1)\) 完全染黑,所以 \(v\) 一定是以 \(u\) 为树根,深度最深的那个儿子(也就是长链剖分的长儿子)
然后记 \(f_u\) 表示以 \(u\) 为根的最长链长度和 \(g_u\) 表示除开那个儿子的最长链(也就是次长链),那么就有 \(d \le \min(f_u-1,g_u+1)\) ( \(d<f_u\) 是因为钦定了不能把整棵树染黑)
那么接下来考虑有些点不能选的情况,首先有能选的点没有任何影响,主要考虑不能选的点还能有哪些贡献
可以发现上界不变,但有下界,注意如果 \(f_(u,d)\) 至少有一个其中有关键点的子树被全染黑了,那么 \(f(u,d)\) 一定能被表示出来,且如果不存在就一定表示不出来,所以下界就是其中有关键点的子树中最小的最深深度
证明也不难,假设存在一个 \(x\) 使得 \(f(x,d')=f(u,d)\) ,令其所在的子树根为 \(v\) 。因为 \(v\) 子树没被完全覆盖,所以 \(d'=d-dist(u,x)<d\) (因为没完全覆盖,所以 \(d'\) 大一点或者小一点都有影响),又因为 \(f(u,d)\) 本身要有贡献,所以不存在 \(f(x,d')=f(u,d) \quad (d'<d)\) ,矛盾
换根 \(\text{DP}\) 即可,时间复杂度 \(O(n)\)
AGC019
不知道能不能略
AGC019F Yes or No
AGC022
不知道能不能略
AGC022D Shopping
首先显然可以将时间都对 \(2L\) 取模,模掉的一定要加且不会影响策略,现在有 \(0 \le t_i < 2L\)
先定一个上界 \(2L(n+1)\) (也就是每过 \(2L\) 时间就到下一站,最后回来),然后试图减少一些轮数
我们称在 \(0 \rightarrow L\) 的时候上下车称为在左边上下车,反过来称作在右边上下车,将所有的点分为几种:
在哪边下都会错过另一边的第一趟的点
在左边下会错过右边第一趟的点
在右边下会错过左边第一趟的点
在哪边下都不会错过另一边第一趟的点
第一种点显然没有任何影响,注意对于 \(t_i=0\) 的可以不用多走一轮即可
我们试图让剩下的一些点不多走轮数,具体的形如下图的蓝色和紫色(注意这个图左右反过来了):
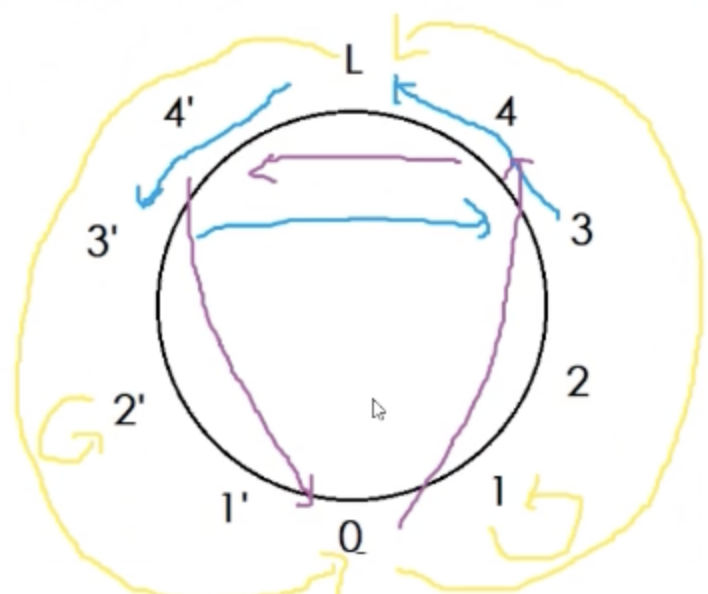
所以我们发现若是存在一对 \(i,j (i<j)\) ,\(i\) 从右边下车能赶上左边第一趟车, \(j\) 从左边下车能赶上右边第一趟车,那么就能减少一轮
于是乎这变成了最大化匹配数,跑网络流?其实不需要,我们观察一下第二种点和第三种点的限制条件
第二种点的限制条件为 \(2(L-x_i) < t_i \le 2x_i\) ,第三种为 \(2x_i < t_i \le 2(L-x_i)\) ,可得第二种点 \(x_i > \frac{L}{2}\) ,第三种点 \(x_i < \frac{L}{2}\)
所以第二种与第三种点必定不会匹配,只有可能是第四种点匹配后三种点,所以先尽量用第四种匹配完其他两种,剩下的自行匹配即可,只需要栈就能维护,时间复杂度 \(O(n)\)
AGC022F Checkers
sto \(\text{w}\color{red}{\text{angrx}}\) orz
若两点 \(A,B\) 进行操作,那么视作删掉了原本两点,加入了 \(C=2B-A\)
故显然最后剩下的点坐标一定形如 \(\sum_{i=1}^n c_i2^{d_i}x^i\) ,由于每个点坐标相差过大,能够看作若 \(x\) 次数不同则不会互相影响,所以其实方案数就是不同的 \(c_i,d_i\) 的方案数
我们考虑倒着来,最开始只有一个点,每次可以把这个点变为两个点,注意到 \((c_i,d_i)\) 只有 \(2n\) 种取值,如果相同我们一起考虑,则可以画成一张 \(n\) 行 \(2\) 列的图
左边一列代表 \(c=1\) ,右边一列代表 \(c=-1\) ,从下往上第 \(i\) 行(最下面为第 \(0\) 行)代表 \(d=2^i\) ,显然最开始只有一个点时其在第 \(0\) 行,左边一列上
那么一次操作等价于把一个点变为两个点,一个在原本点上面的位置,一个在其右边的位置,我们从下往上对于一个等价类一起考虑
注意到具体层数并不重要,设计状态 \(f_{i,a,b}\) 表示还剩 \(i\) 个点,这一层现在左边有 \(a\) 个点,右边有 \(b\) 个点(这一层上面还没拓展,个数都为 \(0\) )
那么我们枚举其上面一层左边要有 \(a'\) 个点,右边要有 \(b'\) 个点(不能同时为 \(0\) ),显然这从前者到后者只有唯一的方法,即左边点变掉 \(a'\) 个点,右边变掉 \(b'\) 个点
那么当前层就变为了左边有 \(a-a'+b'\) ,右边有 \(b-b'+a'\) 个点,而且不会再发生改变,故直接可重排计算一下方案数,然后记搜即可,时间复杂度 \(O(n^5)\) (非常跑不满),可以通过此题
能不能再给力点?
当然可以!
我们先把多重排上面的 \(n!\) 提出来,答案就是 \(n! f_{n-1,1,0}\) ,写出转移
我们设 \(g_{i,D}=\sum_{a-b=D} f_{i-a-b,a,b}\) (显然 \(g_{i,-D}=g_{i,D}\) ),转移做 \(f \rightarrow g,g \rightarrow f\) 复杂度就是 \(O(n^4)\) 了,为啥? \(f\) 状态数为 \(O(n^3)\) ,转移为 \(O(n)\) ,\(g\) 状态数为 \(O(n^2)\) ,转移为 \(O(n)\) ,故计算 \(f\) 为 \(O(n^4)\)
能不能再给力点?
发现 \(g \rightarrow f\) 这一步其实没有用,直接把 \(f\) 删掉,现在答案就变成了 \(n!(g_{n-1,0}+g_{n-1,1})\) ,此时边界为 \(g_{0,D}=[D=0]\) ,转移变为了
复杂度虽然没有得到优化,但是至少现在只剩 \(g\) 了,为了方便,在后面直接将其作为新的 \(f\) ,然后考虑换元,令 \(x=a-D',y=b+D'\) ,则有
分类讨论一下 \(D'\) 的正负号(下面的 \(f_{i,D}\) 都是一部分)
若 \(D'=0\) ,都不需要换元,直接转移即可
若 \(D'>0\) ,则
令
可以做到 \(O(n^3)\) 求解 \(g\) ,然后有
当 \(D'<0\) ,同理可设出一个 \(h\) ,然而发现其将 \(D,D'\) 一并取反就是 \(g\)
所以最后有转移式
记搜即可,时间复杂度 \(O(n^3)\)
AGC029
不知道能不能略
AGC029E Wandering TKHS
引用 \(\text{F}\color{red}{\text{Zzzz}}\) 一句话:
看起来每一步都很显然但是放一起就是一步都不会.jpg
只能说确实,反正我没有脑子
考虑计算点 \(v\) 对 \(u\) 的贡献,因为 \(u\) 肯定会先拓展到以 \(1\) 为根的 \(LCA(u,v)\) ,可以发现若是 \(v\) 对 \(lca\) 有贡献,那对 \(u\) 必定有贡献,所以只需考虑 \(v\) 的祖先
现在 \(u\) 是 \(v\) 的祖先,什么样的情况会使得 \(u\) 在拓展到 \(1\) 之前拓展到 \(v\) 的,思考一下能得到当且仅当 \(1\) 到 \(u\) 路径(不包括 \(u\) )上的最大值大于 \(u\) 到 \(v\) 路径(不包括 \(u\) )上的最大值
那么我们记 \(Max\) 为 \(1\) 到 \(v\) 路径上的最大值,显然 \(Max\) 往 \(v\) 这个方向的子树都可以算上 \(v\) 的贡献,而且当路径上的次大值 \(Maxc\) 满足 \(dep_{Maxc}<dep_{Max}\) 时以 \(Max\) 子树内都能算上 \(v\) 的贡献,这显然可以 \(O(n)\) 计算
AGC038
不知道能不能略
AGC038F Two Permutations
比较小清新的 \(F\) 题,先只考虑 \(A\) 与 \(P\) 的关系,推一推可以发现,对于一个 \(P\) 上的置换环, \(A\) 在这些位置上要么同时选 \(P_i\) ,要么同时不选 \(P_i\) , \(B\) 与 \(Q\) 的关系也同理
所以每个置换环都只有两种状态,且同一个排列中不同置换环互不影响,可以讨论一下每个位置换不换的代价(懒得列举了,具体可以看代码)
但是我们发现若是直接最小割,也就是连向 \(S\) 就同时选的话不好构造图,我们让对应 \(P\) 上的置换环是这样, \(Q\) 上的置换环改为连向 \(T\) 就同时选,就可以建图了,具体还是可以看代码
AGC051
不知道能不能略
AGC051C Flipper
先看能到达的状态有哪些,如果将黑色表示为 \(1\) 白色为 \(0\) ,考虑一次操作对每行每列的异或值的影响
对于每列是平凡的,因为每次操作都会改变一列的异或上 \(0\) 或者 \(2\) ,所以列的限制就是每列异或值相等,我们称第 \(y\) 列的异或值为 \(p_y\)
对于每行就比较难搞,考虑把每行再按列编号 \(\bmod 3\) 的分类,第 \(i\) 行的叫做 \(q_{x,0/1/2}\) ,可以发现每次操作就是把 \(q_{x,*},q_{x+1,*}\) 全部异或 \(1\) ,也就是全部取反
由于行的限制过于强,我们只好大胆猜测个较松的判定:如果两个状态 \(p\) 全相等, \(q_x\) 要么相等,要么取反后相等,那么这两个状态就可以互相到达
证明?可以考虑先把 \(x \ge 2,y \ge 3\) 的黑点全部消成白色,然后按照 \(x=2\) 和 \(y=3\) 把第一象限分成四个区域讨论,发现每个区域都成立,具体的可以看这里 (其实具体的题解都可以看这里)
那么我们考虑对于一个合法的 \(p\) 和 \(q\) ,它对应的状态中最小的点数是多少,我们可以先搞出个下界 \(\sum\limits_{i=0}^2\max(\sum\limits_{y \equiv i \pmod 3}p_y,\sum\limits_x p_{x,i})\) ,显然至少要这么多,接着我们给出一个下界的构造
首先声明,我们称一个 \(p\) 和 \(q\) 是合法的,当且仅当 \(\forall i \in \{0,1,2\} \oplus_{y \equiv i \pmod 3}p_y = \oplus_x q_{x,i}\) ,原因显然
然后对于 \(p_y=1\) 且 \(q_{x,y \pmod 3}=1\) 的,我们可以直接让 \((x,y)\) 为黑色,当只满足一个条件时我们考虑找到一个空行 \(X\) 和一个空列 \(Y\) ,即 \(p_Y=0,q_{X,*}=0\) ,然后把点按照条件放置于 \((x,Y)\) 或 \((X,y)\) ,由于 \(p\) 和 \(q\) 合法,可以推出这一空行和这一空列的所有异或值仍为 \(0\)
我们令 \(a_i=\sum\limits_{y \equiv i \pmod 3}p_y,b_i=\sum\limits_x p_{x,i}\) ,那么一次操作只会对 \(b\) 有所修改,而我们要求的是 \(\sum\limits_{i=0}^2\max(a_i,b_i)\) ,所以将答案式改写为 \(\sum\limits_{i=0}^2a_i+\max(b_i-a_i,0)\) ,我们相当于要最小化 \(\sum\limits_{i=0}^2\max(b_i-a_i,0)\)
我们先假设可以做到把所有的 \(q_{x,*}\) 中至多只有一个值为 \(1\) ,那么接下来我们每次将一个值为 \(1\) 的行翻转,对应的是将 \(b\) 中一个大于等于 \(0\) 的位置的值减 \(1\) ,其他两个位置的值加 \(1\) ,那么贪心一下肯定是将 \(b_i-a_i\) 中的最大值减到 \(0\) 或者次大值加到 \(0\) 时是最优的,计算一下即可
问题是我们不一定能够做到先前那个条件啊?可以发现合法等价于 \(b_i-a_i \equiv 0 \pmod 2\) ,所以只要多操作一次就可以了,能够发现这顶多让答案增加了 \(1\) ,可以证明这是最优的(虽然我不会)
AGC055
AB 略
AGC055E Set Merging
题目太离谱,怎么办?快来直接摆烂!/ll
发现原操作太离谱,来点等价的东东,又因为 \(S_i\) 和 \(S_{i+1}\) 相等的时候对 \(i\) 操作没用,我们加强限制,直接不允许这样做,然后离谱的构造来了
我们把初始状态视作一个 \(\{1,2,...,n\}\) 的排列,对 \(i\) 操作视作 \(\text{swap}(p_i,p_{i+1})\) (有条件 \(p_i<p_{i+1}\) ),有 \(S_i=\big[\min\limits_{j=i}^{n}p_j,\max\limits_{j=1}^{i} p_j \big]\) ,证明可以考虑归纳
所以只要能构造出一个这样的排列,那么操作数就是逆序对数,考虑如何构造,我们先把一定要放特定数的位置 \(i\) 先放好,如果这一步满足条件,剩下的数从下到大放肯定最容易合法且逆序对数最小,所以搞一搞就可以了,具体实现可以看看代码
AGC056
不知道能不能略
AGC056C 01 Balanced
我们将 \(\texttt{0}\) 的权值赋为 \(1\) , \(\texttt{1}\) 的权值赋为 \(-1\) ,记 \(S_i\) 为其权值前缀和,显然有限制
绝对值很难搞,但是可以发现可以把第一个限制变为 \(|S_i-S_{i-1}| \le 1\) ,因为没有限制会影响 \(S_i\) 的奇偶性,所以就是 \(01\) 最短路
AGC056D Subset Sum Game
博弈博弈,完全自闭/ll
我们发现 \(\text{Alice}\) 先手被 \(\text{Bob}\) 狙击实在太毒瘤了,考虑先枚举 \(\text{Alice}\) 先选第 \(i\) 个数 \(a_i\) ,然后变成 \(\text{Bob}\) 先手, \(\text{Alice}\) 负责凑即可
按照 \(\text{z}\color{red}{\text{houhuanyi}}\) 的说法, \(\text{I}\color{red}{\text{tst}}\) 曾这样总结过一个套路,双人取数和一些双人博弈,可以找一些匹配 \((x,y)\) ,表示如果 \(\text{Alice}\) 选 \(x\) ,则 \(\text{Bob}\) 选 \(y\) ,反之若 \(\text{Alice}\) 选 \(y\) 则 \(\text{Bob}\) 就选 \(x\)
先考虑 \(n\) 是奇数,在选了一个数后就变成了偶数个,我们将其排序以后奇数位置与偶数位置(除去了第 \(i\) 个位置后)匹配,那么判定条件就是( \(X\) 是奇数位置的和, \(Y\) 是偶数位置的和,显然有 \(X \le Y\) )
如果不满足则 \(\text{Bob}\) 可以往不合法的一边逼,比如 \(X+a_i < L\) ,那么 \(\text{Bob}\) 每次选当前最大的偶数位置的,如果 \(\text{Alice}\) 不按套路出牌也选偶数位置(因为按套路肯定输了),那么 \(\text{Bob}\) 直接把最大的奇数位置也选了,那么此时 \(\text{Alice}\) 拥有的数的和更小了
如果满足就代表对于每个匹配任选一个数加起来都在范围内,所以充分必要
偶数咋做?暴猜结论!枚举不管一个数再套奇数做法就切了!
证明相似,不管的那个数就是 \(\text{Bob}\) 的先手切换器(因为这个数没有匹配,所以 \(\text{Alice}\) 不会管这个数),这次选了这个数下次就是 \(\text{Alice}\) 先手在配对的组里选了,因为上述判定条件就等价于怎么选都满足条件,所以 \(\text{Alice}\) 接下来随便选一个数,如果 \(\text{Bob}\) 选了这个数的匹配,那就是一个子问题,否则就选和 \(\text{Bob}\) 选的数匹配的一直选到 \(\text{Bob}\) 选与随便选的那个数匹配的即可,又是子问题,所以一定能在每个匹配对中选一个,也就满足条件, \(\text{Bob}\) 先手时直接选与 \(\text{Bob}\) 这轮匹配的数即可,这是充分性
必要性的话考虑不满足的话 \(\text{Bob}\) 像奇数一样逼输 \(\text{Alice}\) 就行了,所以又是充分必要的
UPD :更新一个线性做法,这个做法可能还自然一些
首先 \(n\) 是奇数的时候已经是线性了,只考虑偶数怎么做到线性,重新观察限制的式子 \(L \le S_A \le R\) ,我们将其乘 \(2\) 再同时减去所有数之和 \(S\) ,有 \(2L-S \le S_A - S_B \le 2R-S\)
令 \(x=S-(L+R)\) ,同时加上 \(x\) ,有 \(L-R \le S_A-S_B+x \le R-L\) ,即为 \(|S_A-S_B+x| \le R-L\) ,就可以转化为为初始有个 \(x\) , \(\text{Alice}\) 每次选一个数 \(a_i\) 可以让其变为 \(x+a_i\) , \(\text{Bob}\) 选 \(a_i\) 则可以让其变为 \(x-a_i\) , \(\text{Alice}\) 想最小化最后的 \(x\) 的绝对值, \(\text{Bob}\) 要最大化,问 \(x\) 最后的值为多少
首先还是因为 \(\text{Alice}\) 不想被狙击,所以 \(\text{Alice}\) 先选一个 \(a_p\) ,把先手交给 \(\text{Bob}\) ,然后可以发现一个上界是将 \(a_p+x\) 放进删掉一开始选的那个数的序列中,排完序后偶位置之和减去奇位置之和,然后发现这也是下界
具体证明可以考虑归纳法,其实和上面那个做法的证明差不多,还是匹配,我们还是排完序后那样匹配,但是 \(x+a_p\) 匹配的那个相当于是没有匹配的
如果 \(\text{Bob}\) 选中的是这个没有匹配的,则 \(\text{Alice}\) 就选择最大的位置,变为子问题;否则 \(\text{Alice}\) 还是选择 \(\text{Bob}\) 选的数的匹配即可,可以发现上界即把每个匹配都取满,且 \(\text{Bob}\) 确实能取满
所以枚举一下 \(p\) 加上双指针,就能像 \(n\) 是奇数一样做到 \(O(n)\) 了
AGC057
AB 略
AGC057C Increment or Xor
$\text{AGC}$ 构造题果真都是神仙题/ll
看到异或和加 $1$ 操作,考虑建一棵从低到高的 $\text{01trie}$ ,叶子的 $val$ 记的是这个叶子代表的值的位置,观察一下两个操作:
我们发现叶子要进行 $val$ 的交换必须 $\oplus 2^{n-1}$ 把所有叶子交换 ,或者 $+1$ 实现 $2^n-1$ 值对应的叶子和 $2^{n-1}-1$ 值对应的叶子交换 ,想交换任意一对叶子就先把它们 $\oplus$ 成 $2^n-1$ 和 $2^{n-1}-1$ 即可
因为与一个叶子同父亲的另一个叶子永远不变,所以我们想的算法是先将所有叶子交换成 $val$ 小的是左儿子,然后所有数 $\oplus$ 上 $A_0$ 现在的值,然后 $\text{check}$ 一下即可
正确性比较显然,可以感性证明?然后时间复杂度是 $O(n2^n)$ 的(有个 $\text{01trie}$ ),可能有个细节就是怎么查一对叶子现在的权值,就直接暴跳父亲看是左儿子还是右儿子即可,记得传标记!
操作数至多为 $2^n+O(1)$ 的,但是我们可以卡卡常,看是 $val_{ls}<val_{rs}$ 和 $val_{ls}>val_{rs}$ 哪个多,先都变成那个状态,可以发现 $\oplus a_0$ 时会顺便转对,就变成 $2^{n-1}+O(1)$ 的了
ARC 做题简记
[ARC136F] Flip Cells
生成函数做法还不会,不过有一个 \(\text{HEZ}\) 神仙的做法,记录一下
其实和 CF1349D 的官方题解做法(非鞅与停时做法)思想几乎一致,所以无论什么做法都有着不同的拓展性,不要觉得一个做法就能涵盖另一个做法
先考虑如果指定一个终止态怎么求?那么其实就可以转化为长度为 \(N\) 的 \(01\) 序列,现在有 \(x\) 个位置为 \(1\) ,每次可以随机一个位置将其反转,求所有位置都为 \(0\) 的期望时间
设 \(f_i\) 为现在有 \(i\) 个 \(1\) ,到所有位置为 \(0\) 的期望时间,那么有转移
这非常的经典,我们考虑记 \(g_i=f_{i+1}-f_{i}\) ,有
又因为 \(f_{N}=f_{N-1}+1\) ,所以 \(g_{N-1}=1\) ,即可以推出所有的 \(g\) ,也就可以求出所有的 \(f\)
现在回到原问题,有多个终止状态怎么搞?考虑 CF1349D 的官方题解做法
令 \(S\) 为整个终止态集合,状态 \(i\) 表示编号为 \(i\) 的终止态(随便编号)
设 \(end_i\) 为终止态只有状态 \(i\) 时的期望时间, \(ans_i\) 为原题意中结束在状态 \(i\) 的期望时间, \(p_i\) 为结束在 \(i\) 的概率, \(trans_{i,j}\) 为初始状态为 \(i\) ,终止状态只有 \(j\) 的期望时间,则有
求和得到
注意到对于任意的 \(i\) , \(\sum\limits_{j=1}^{|S|}trans_{i,j}\) 都相等,设其为 \(C\)
\(|S|\) 是好求的,现在只需要求 \(\sum\limits_{i=1}^{|S|}end_{i}\) 和 \(C\) 了,其实是两个一样的问题,第一个初始态是题目给的,第二个随便搞个终止态(原题意里的终止态)当初始态即可
因为只跟 \(1\) 的个数有关,可以背包解决,时间复杂度 \(O(n^2m^2)\)
咕咕咕~



 浙公网安备 33010602011771号
浙公网安备 33010602011771号