实验3_C语言函数应用编程

一、实验目的

1. 能正确使用c语法规则定义、声明、调用函数
2. 能正确编写递归函数
3. 针对具体问题场景，能合理抽象出独立的功能模块，正确定义函数并使用，使得代码更具可读性、可维护性
4. 针对具体问题场景，能正确、合理使用全局变量和局部static变量，解决实际问题

二、实验过程
1、task1：成绩等级转换
源代码：

#include <stdio.h>

char score_to_grade(int score);  // 函数声明

int main() {
    int score;
    char grade;

    while (scanf_s("%d", &score) != EOF) {
        grade = score_to_grade(score);  // 函数调用
        printf("分数: %d, 等级: %c\n\n", score, grade);
    }

    return 0;
}

// 函数定义
char score_to_grade(int score) {
    char ans;

    switch (score / 10) {
    case 10:
    case 9:   ans = 'A'; break;
    case 8:   ans = 'B'; break;
    case 7:   ans = 'C'; break;
    case 6:   ans = 'D'; break;
    default:  ans = 'E';
    }

    return ans;
}

运行结果：

问题回答：

问题1：函数 score_to_grade 的功能是什么？形参类型、返回值类型是什么？

答：将输入的分数（score）转换为对应的等级（grade）。根据分数的区间，它将分数分为A，B，C，D或E等级。

形参类型：该参数为 int 类型，表示分数。返回值类型：函数返回一个 char 类型的值，表示对应分数的等级（如 'A', 'B', 'C', 'D', 或 'E'）。

问题2：如果line21-28以下形式，代码存在哪些问题，请逐一指出。

 switch(score/10) {
 case 10:
 case 9:   ans = "A"; 
case 8:   ans = "B";
 case 7:   ans = "C";
 case 6:   ans = "D";
 default:  ans = 'E';
 }

答：① 字符串和字符的类型不匹配：ans = "A"; 等行使用的双引号表示字符串类型，而字符类型应该使用单引号，例如 ans = 'A';

② 缺少 break 语句：在每个 case 后面缺少 break 语句，满足某个 case 条件后，代码会继续执行后面的所有 case ，直到遇到 break 或 switch 结束，这将导致错误的等级被赋值。例如，如果 score 是 89，程序会执行到 case 8；并给 ans 赋值为 B ，然后继续执行，最后会赋值为 E 。

2、task2：计算一个整数 n 所有数字的和

源代码：

#include <stdio.h>
int sum_digits(int n);  // 函数声明
int main() {
    int n;
    int ans;
    while (printf("Enter n: "), scanf_s("%d", &n) != EOF) {
        ans = sum_digits(n);    // 函数调用
        printf("n = %d, ans = %d\n\n", n, ans);
    }
    return 0;
} 

// 函数定义
int sum_digits(int n) {
    int ans = 0;
    while (n != 0) {
        ans += n % 10;
        n /= 10;
    }
    return ans;
}

运行结果：

问题回答：

问题1：函数sum_digits的功能是什么？

答：计算并返回一个整数 n 的所有数字的和。例如，给定 n = 123，该函数会返回 1 + 2 + 3 = 6。它通过逐位提取数字（使用 n % 10）并累加这些数字实现这个功能，直到 n 减少到 0 为止。

问题2：如果保持main代码和函数sum_digits声明不变，把函数sum_digits定义成如下实现方式，能实现同 等的效果吗？ 如果不能实现同等效果，分析原因。 如果能实现同等效果，说明两种实现方式背后的算法思维区别。

 int sum_digits(int n) {
    if(n < 10)
        return n;
    
    return sum_digits(n/10) + n%10;
 }

答：能实现同等效果。第一种是迭代方式：使用 while 循环，通过逐位提取数字的方式（n % 10）来累加数字，直到 n 变为 0。 这种方式在逻辑上是通过直接操作数的每一位来处理问题，通常更容易理解，且避免了递归的调用开销。 第二种是递归方式：使用递归方法 essentially calling itself with a smaller number (i.e., n / 10) until the number is less than 10. 这种方式有助于利用递归的特性，从数学角度思考问题，将复杂问题分解为更简单的部分。 递归实现可能在某些情况下易于表达（如单一表达式），但在深度递归时可能会因栈溢出而遭遇性能问题，尤其是对于大数字。

3、task3：计算整数 x 的 n 次方
源代码：

#include <stdio.h>

int power(int x, int n);    // 函数声明

int main() {
    int x, n;
    int ans;

    while (printf("Enter x and n: "), scanf_s("%d%d", &x, &n) != EOF) {
        ans = power(x, n);  // 函数调用
        printf("n = %d, ans = %d\n\n", n, ans);
    }

    return 0;
}

// 函数定义
int power(int x, int n) {
    int t;

    if (n == 0)
        return 1;
    else if (n % 2)
        return x * power(x, n - 1);
    else {
        t = power(x, n / 2);
        return t * t;
    }
}

运行结果：

问题回答：

问题1: 函数power的功能是什么？

答：函数 power 的功能是计算给定整数 x 的 n 次方，即 xn。

问题2：函数power是递归函数吗？如果是，找出递归模式。写出这个递归模式对应的数学公式模型。

答：函数 power 是一个递归函数。数学公式模型：

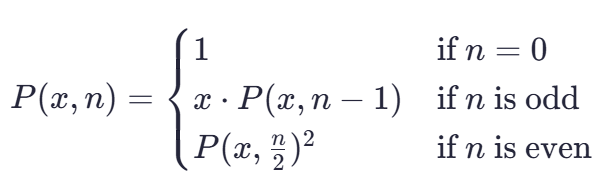
 4、task4：打印100以内的孪生素数及其总数

源代码：

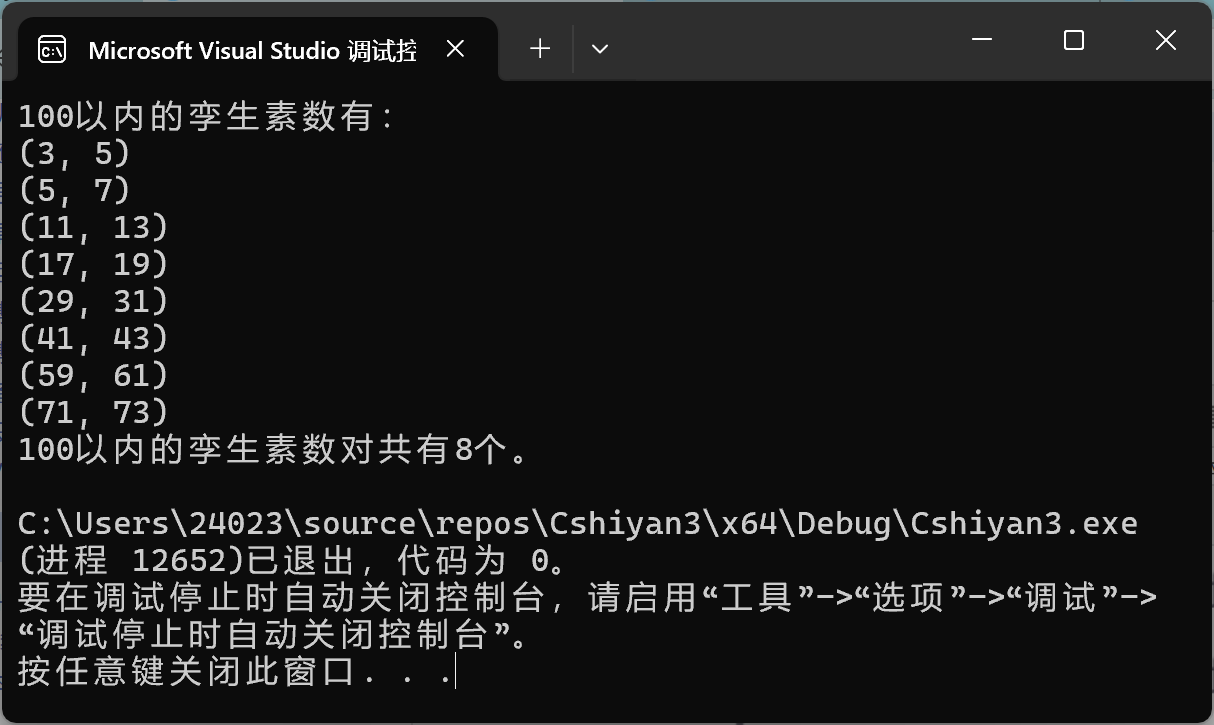
#include <stdio.h>  

// 函数声明  
int is_prime(int n);

int main() {
    int n;
    int count = 0; // 孪生素数的总数  
    printf("100以内的孪生素数有：\n");

    // 检查2到97的数字，判断对应的n和n+2是否为素数  
    for (n = 2; n <= 97; n++) {
        if (is_prime(n) && is_prime(n + 2)) {
            printf("(%d, %d)\n", n, n + 2);
            count++; // 计数  
        }
    }

    // 输出孪生素数对的总数  
    printf("100以内的孪生素数对共有%d个。\n", count);
    return 0;
}

// 判断一个正整数n是否是素数  
int is_prime(int n) {
    if (n <= 1) {
        return 0; // 小于等于1的数字不是素数  
    }
    for (int i = 2; i * i <= n; i++) { // 检查到平方根  
        if (n % i == 0) {
            return 0; // 不是素数  
        }
    }
    return 1; // 是素数  
}

运行结果：

 5、task5：汉诺塔

源代码：

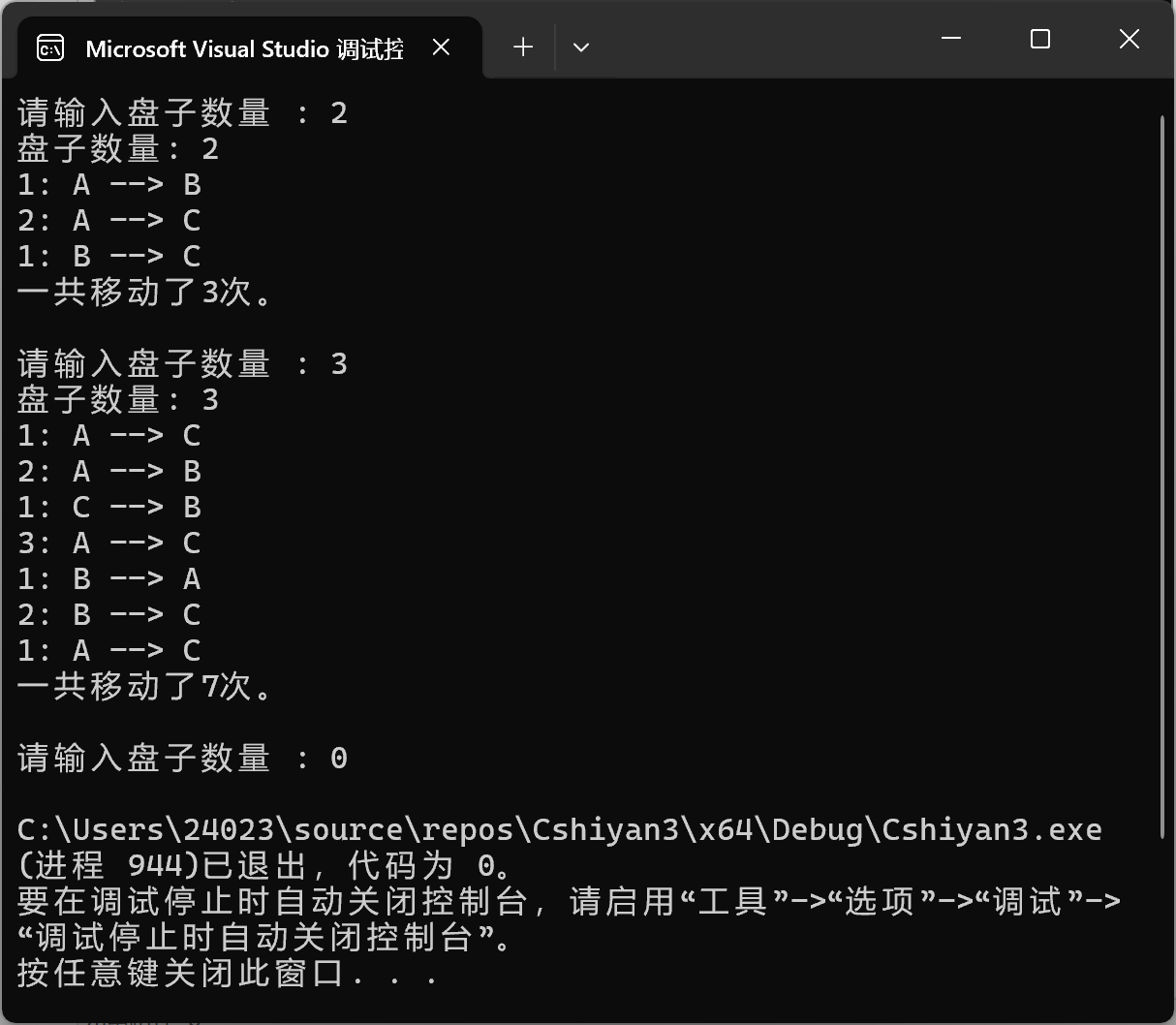
#include <stdio.h>  

void move(int n, char source, char target, char auxiliary, int* count) {
    if (n == 1) {
        // 移动一个盘子并增加移动次数  
        printf("1: %c --> %c\n", source, target);
        (*count)++;
    }
    else {
        // 递归移动n-1个盘子  
        move(n - 1, source, auxiliary, target, count);
        // 移动最后一个盘子  
        printf("%d: %c --> %c\n", n, source, target);
        (*count)++;
        // 递归移动n-1个盘子  
        move(n - 1, auxiliary, target, source, count);
    }
}

int main() {
    int n;
    while (1) {
        printf("请输入盘子数量 : ");
        scanf_s("%d", &n);
        if (n == 0) {
            break;
        }

        int moveCount = 0; // 初始化移动次数  

        printf("盘子数量: %d\n", n);
        move(n, 'A', 'C', 'B', &moveCount); // 从A到C，使用B作辅助  
        printf("一共移动了%d次。\n\n", moveCount);
    }

    return 0;
}

运行结果：

 6、task6：分别用迭代方式和递归方式编写函数计算组合数

源代码：

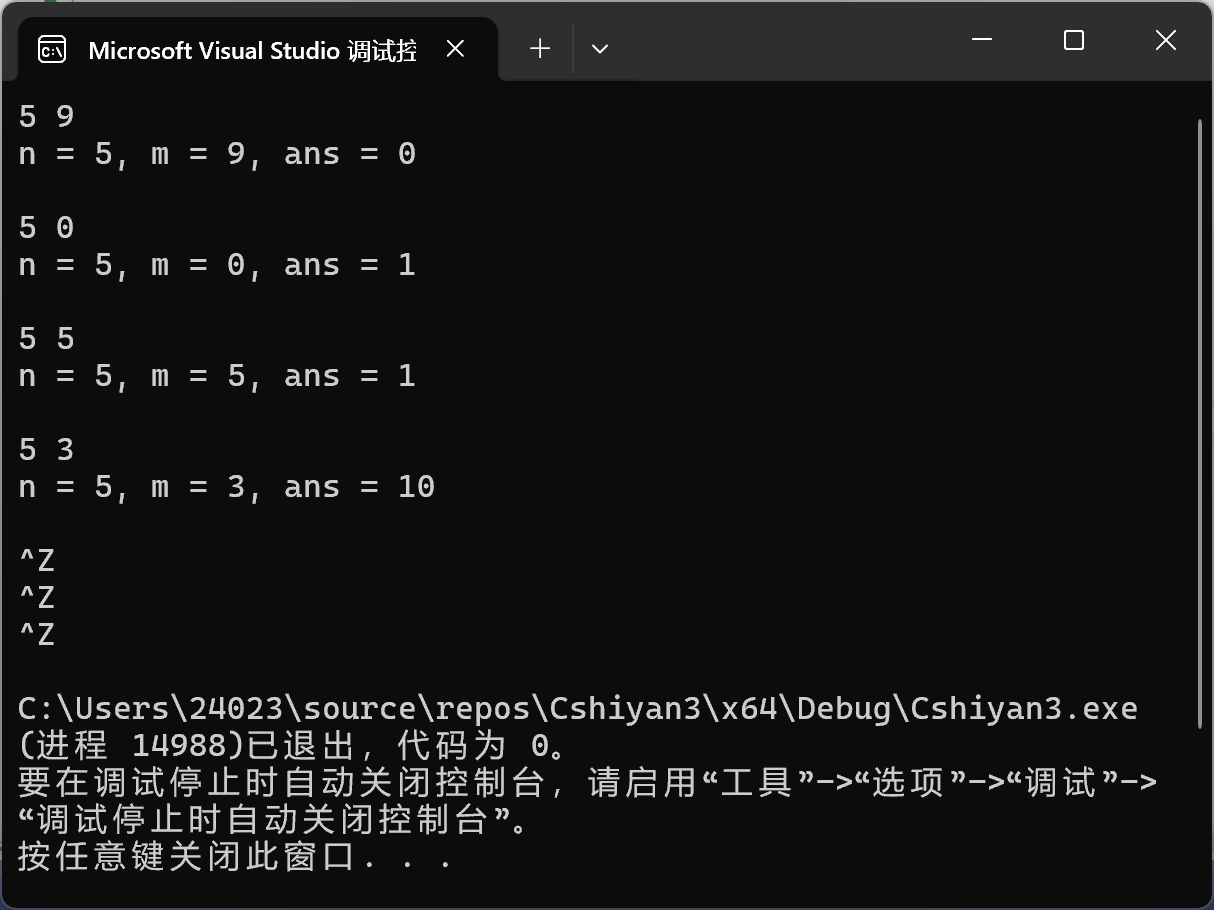
#include <stdio.h>  

int func(int n, int m);   // 函数声明  

int main() {
    int n, m;
    int ans;

    while (scanf_s("%d%d", &n, &m) != EOF) {
        ans = func(n, m);   // 函数调用  
        printf("n = %d, m = %d, ans = %d\n\n", n, m, ans);
    }

    return 0;
}

// 迭代方式实现组合数计算  
int combination_iterative(int n, int m) {
    if (m > n || m < 0) {
        return 0;
    }
    if (m == 0 || m == n) {
        return 1;
    }

    int result = 1;

    // 计算 C(n, m) = n! / (m! * (n - m)!)  
    for (int i = 0; i < m; i++) {
        result = result * (n - i) / (i + 1);
    }

    return result;
}

// 递归方式实现组合数计算  
int combination_recursive(int n, int m) {
    if (m > n || m < 0) {
        return 0;
    }
    if (m == 0 || m == n) {
        return 1;
    }
    // C(n, m) = C(n-1, m-1) + C(n-1, m)  
    return combination_recursive(n - 1, m - 1) + combination_recursive(n - 1, m);
}

// 主函数实现  
int func(int n, int m) {
    // 可以在这里选择使用哪种实现方法  
    // return combination_iterative(n, m);    // 使用迭代方式  
    return combination_recursive(n, m);        // 使用递归方式  
}

运行结果：

7、task7：用穷举法计算三个整数的最大公约数
源代码：

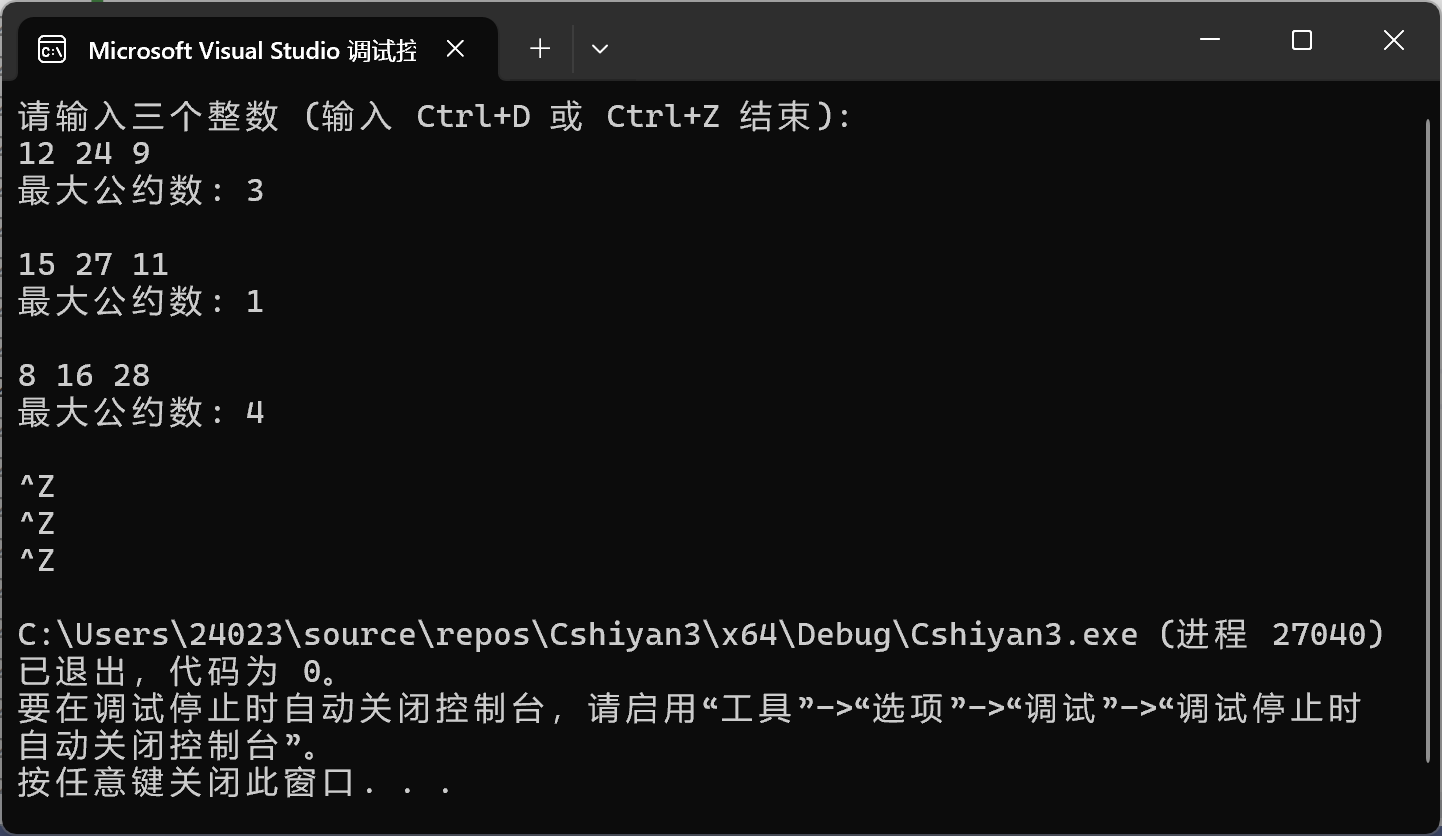
#include <stdio.h>  

// 函数声明  
int gcd(int a, int b, int c);

int main() {
    int a, b, c;
    int ans;
    printf("请输入三个整数 (输入 Ctrl+D 或 Ctrl+Z 结束):\n");
    while (scanf_s("%d%d%d", &a, &b, &c) != EOF) {
        ans = gcd(a, b, c);  // 函数调用  
        printf("最大公约数: %d\n\n", ans);
    }
    return 0;
}

// 函数定义  
int gcd(int a, int b, int c) {
    int min_num = a;
    if (b < min_num) min_num = b;
    if (c < min_num) min_num = c;

    for (int i = min_num; i > 0; i--) {
        if (a % i == 0 && b % i == 0 && c % i == 0) {
            return i;  // 找到最大公约数后立即返回  
        }
    }
    return 1;  // 如果没有找到大于1的公约数，返回1  
}

运行结果：

 三、实验心得

1、双引号表示字符串类型，单引号表示字符类型。

2、写程序先搭好框架，再按照算法填入相应的代码，运行调试。

3、程序错误大致有三种：算法错误、语法错误、运行结果与预期不符。