【攻防世界】-Simple-Math

⭕、知识点

伽罗瓦域/暴力求解/脚本编写

一、题目

二、解题

直接写脚本

import numpy as np
import galois
import hashlib

# 定义二元伽罗瓦域
GF = galois.GF(2)

# 定义题目中的矩阵
A = GF([[1, 1, 0, 1, 1, 0, 1, 1, 1, 1],
        [0, 0, 1, 1, 0, 0, 0, 1, 1, 0],
        [1, 0, 1, 1, 0, 0, 1, 1, 1, 0],
        [0, 1, 0, 1, 0, 1, 1, 1, 0, 0],
        [0, 0, 0, 0, 1, 1, 0, 1, 1, 1],
        [1, 1, 1, 1, 1, 0, 0, 0, 1, 0],
        [1, 0, 0, 0, 0, 1, 0, 1, 1, 1],
        [0, 0, 0, 1, 0, 1, 0, 0, 0, 1],
        [0, 1, 1, 0, 0, 0, 1, 1, 1, 0],
        [0, 0, 0, 1, 0, 0, 1, 1, 0, 1]])

# 求A的逆
A_inv = np.linalg.inv(A)
# 定义题目中的矩阵b
b = GF([1, 0, 1, 1, 0, 0, 0, 1, 0, 1])
# 求解线性方程组
x = A_inv@b
# 打印结果
print(x)
# 合并x向量中的所有元素
x_c = "".join(map(str, x))
# 计算哈希值
hash_code = hashlib.sha1(x_c.encode())
# 转为十六进制表示，得到结果
result = hash_code.hexdigest()
print(result)

三、答案

XSCTF{103c8041593b4b8e38971db283a7a773b0ffc2ee}

四、总结

1、有关伽罗瓦域

2、有关伽罗瓦域的代码

A_inv = np.linalg.inv(A)

np实际上调用了GF的接口，所以可处理A矩阵
如果传入用np自己定义的A矩阵，则np并不知道A是伽罗瓦域矩阵，将会导致逆矩阵计算错误

3、map()函数的使用

# 基本语法
map(function, iterable)

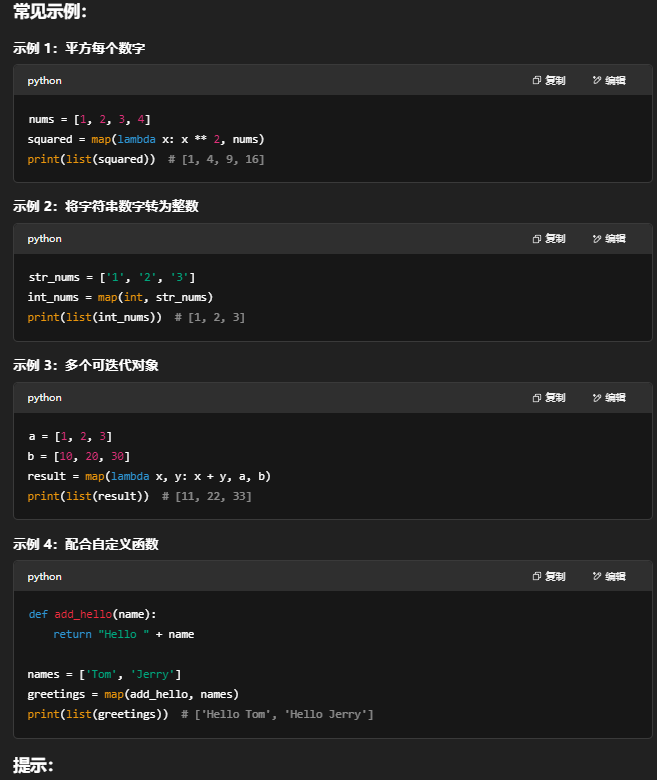
所以代码中map(str, x)是把向量中的每个值转为字符串并保存在一个新的列表

4、np.linalg模块

命名原因：
线性代数（Linear Algebra）

所有线性代数的操作都在本模块中，包括本题中用到的inv()求逆矩阵

5、hashlib的部分函数

sha1()

只能接收字节数据，但是x_c为字符串类型，用.encode()可以将字符串转为字节类型

复习一下,把字符串转为字节数据

byte("xxx",encoding="utf-8")
# 或
"xxx".encode("utf-8)