OO第三单元JML总结

(1)总结分析自己实现规格所采取的设计策略

• 刚开始阅读JML时，由于方法规格过长、需要填空的部分过多感到一点混乱，但是经过通读代码的方式慢慢找到了方法。

• 首先根据需求实现基础的exceptions中的异常类；再完善main中除NetWork类之外的类的属性和大部分方法；最后处理规格更为复杂、与其他类交互最多的NetWork类。

• 在完善类中方法时，首先处理规格中的异常部分，对不同情况进行讨论并快速了解非异常情况；接着，分析规格要求在类中创建或选用合适的容器，实现一种时间复杂度较低的方法。

(2)结合课程内容，整理基于JML规格来设计测试的方法和策略

• 测试方法
  • JUnit：完成一个相对较为复杂的函数后，对照JML对可能出现的情况做测试，测试重点为核心代码（算法的核心部分）和复杂代码（循环、分支部分以及具有特殊限制的代码）
  • 评测机：对指令按照交互关系进行分类，每一类测1000点，一个点10000条指令，出错概率更高
  • 手造数据：一般用来构造极端数据卡TLE
• 测试策略
  • 效率高的算法用于编写代码，之前实现的效率比较低但可以保证正确性的代码可以用来做测试
  • 采用对拍的方法，避免出现对JML理解偏差

(3)总结分析容器选择和使用的经验

• Person类
  • HashMap<Person, Integer> acquaintance;需要查询Person的相关者
  • LinkedList<Message> messages; 加入信息采用头插法，复杂度\(O(1)\)
• Group类
  • HashMap<Integer， Person> people;需要用id索引Person
• Network类
  • HashMap<Integer, Person> personMap;需要用id索引Person
  • SizeBalancedTree<Person> netSbt;查询name rank，复杂度\(O(\log(n))\)；维护节点大小平衡树时间复杂度均摊为\(O(\log(n))\)
  • DisjointSet netSet;查询联通分支数，复杂度\(O(1)\)，判断两节点是否属于同一连通分支，复杂度\(O(1)\)，维护并查集时间复杂度均摊为\(O(1)\)
  • HashMap<Integer, Group> groupMap;需要用id索引Group
  • HashMap<Integer, Message> messageMap;需要用id索引Message
  • HashMap<Integer, HashSet<Integer>> groupPersonSetMap;维护用于getGroupValueSum()方法的类的属性groupValueSum，复杂度\(O(1)\)
  • HashMap<Integer, Integer> emojiId2HeatMap;用于表示emojiId和Heat的映射关系
  • HashMap<Person, HashSet<Edge>> person2EdgeSetMap;作为Person与其acquaintance的value的补充，维护复杂度\(O(1)\)

(4)针对本单元容易出现的性能问题，总结分析原因如果自己作业没有出现，分析自己的设计为何可以避免

• isCircle (qci)： 判断两节点是否处于同一连通分支分支。如果用BFS，DFS暴力遍历person的所有acquaintance，时间复杂度为\(O(n)\)或\(O(n^2)\)；本次作业采用并查集，时间复杂度\(O(1)\)
• queryNameRank (qnr)：求Network中某个人按name排序的排名。如果暴力遍历person，时间复杂度为\(O(n)\)；本次作业采用节点大小平衡树，时间复杂度为\(O(\log(n))\)
• queryBlockSum (qbs)：求解连通分支的个数。如果用BFS，DFS在Network的person中暴力遍历，时间复杂度为\(O(n)\)或\(O(n^2)\)；本次作业采用并查集，时间复杂度\(O(1)\)
• getAgeMean (qgam)：求Group中所有人的年龄的平均值。如果直接遍历该Group中所有的Person求解，时间复杂度为\(O(n)\)；本次作业在Group中添加peopleAgeSum变量来记录组内Person年龄和，在执行addPerson()和delFromGroup()方法时对其进行维护，时间复杂度\(O(1)\)
• getAgeVar (qgav)：求Group中所有人的年龄的方差。如果直接遍历该Group中所有的Person求解，时间复杂度为\(O(n)\)；本次作业在Group中添加peopleAge2Sum变量来记录组内Person年龄平方和，在执行addPerson()和delFromGroup()方法时对其进行维护，时间复杂度\(O(1)\)
• getValueSum (qgvs)：求Group中所有边的边权之和。如果直接对组内的Person进行二重循环遍历求解，时间复杂度为\(O(n^2)\)；本次作业在Group中添加groupValueSum变量来记录边权和，在执行addPerson()、delFromGroup()以及addRelation()方法时在对其进行维护，时间复杂度\(O(1)\)
• sendIndirectMessage (sim)：求带权图两节点间最短路径。如果暴力遍历，时间复杂度为\(O(n)\)或\(O(n^2)\)；本次作业采用堆优的Dijkstra算法，时间复杂度为\(O(\log(n))\)

(5)梳理自己的作业架构设计，特别是图模型构建与维护策略

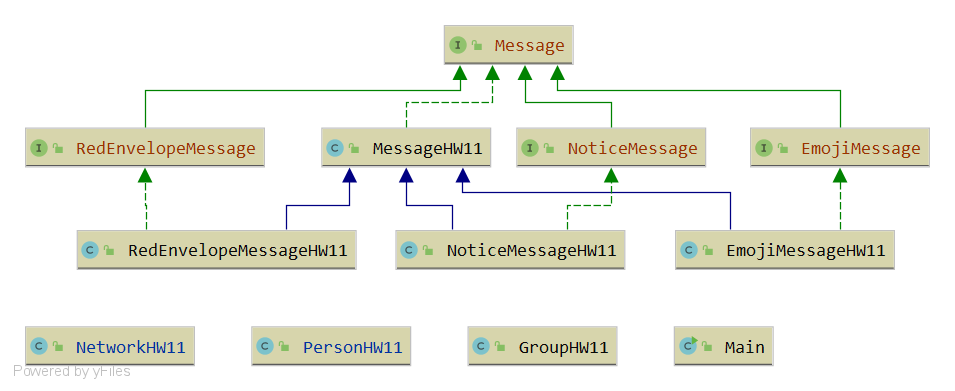
本次作业主要根据所给JML按部就班地实现，并没有特别的架构设计；此外，图模型的构建与维护已经在前文中详细叙述，在此不再赘述。