Towers of Hanoi题解

Towers of Hanoi

题面翻译

给定盘子数\(n\)和步数\(m\),求汉诺塔移动\(m\)步之后，三根柱子上各有多少个盘子。

\(n\)最大为\(100\)，\(m\)最大为\(2^n-1\).

题目描述

PDF

输入格式

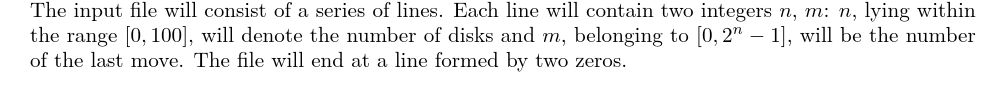
输出格式

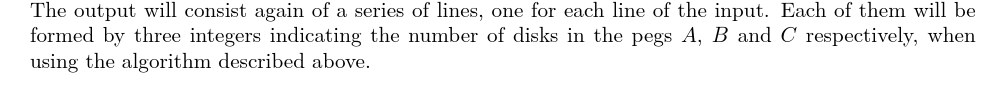
样例 #1

样例输入 #1

3 5
64 2
8 45
0 0

样例输出 #1

1 1 1
62 1 1
4 2 2

题目分析

仔细阅读题面，可知目的为：汉诺塔中 \(n\) 个盘子移动 \(m\)​ 步之后，三根柱子上各有多少个盘子。

首先，汉诺塔问题的递归解决步骤为：

1. 先将上面的 \(n-1\) 个盘子从起点柱子移动到中转柱子。
2. 然后将最底下、最大的盘子从起点柱子移动到目标柱子。
3. 最后将 \(n-1\) 个盘子从中转柱子移动到目标柱子。

代码框架为：

/*
n : 盘子数量
from : 起点柱子
to:目标柱子
tmp:中转柱子
*/
void hanoi(int n,int from,int to,int tmp){
	if(n==1){
		cout<<from<<"->"<<to<<endl;
		return ;
	}
	hanoi(n-1,from,tmp,to);
	hanoi(1,from,to,tmp);
	hanoi(n-1,tmp,to,from);
}

由此，我们可以使用模拟的方式来统计各个柱子上盘子的数量，但是盘子数量最多为 \(100\) 这么递归下去会超时，我们需要找到更快的方法。

从汉诺塔的递归实现，我们来寻找一下执行次数的规律。设 \(f_n\) 为 \(n\) 个盘子的移动次数，从递归的实现过程可得到移动次数的计算公式：\(f_n=f_{n-1}+1+f_{n-1}=2\times f_{n-1}+1\)。且 \(f_1=1\)，手动递推计算一下可发现 \(n\) 个盘子的执行次数为 \(2^n-1\)。

这个发现能否对于程序优化带来帮助呢？

还是回到原始的递归实现汉诺塔的部分，程序分为了 \(3\) 个部分，对于第一部分将 \(n-1\) 个盘子进行移动的部分根据我们刚刚求到的公式可计算出总的执行次数为 \(2^{n-1}-1\)，若步骤数 \(m>2^{n-1}-1\) 我们完全不用去模拟这 \(n-1\) 个盘子的具体移动过程，直接将这 \(n-1\) 个盘子进行整体的移动即可。若是 \(m\le2^{n-1}-1\) 则第三步移动 \(n-1\) 个盘子从中转柱子到目标柱子的部分也不用去做了，因为执行不到那就会有 \(m\) 次了。

依据这样的思路，不断缩小问题的规模，直到计算出执行次数为 \(m\) 位置，我们可以采用递归的方式进行实现。

另外题目中注意一些易错的细节，首先是数据范围，\(m\) 最多为 \(2^n-1\) 会超过 long long 我们可以使用 __int128 来进行存储；其次是注意题目中要求盘子总数是偶数时正常从A到C，而总数为奇数时则是从A到B通过C中转。

代码实现

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
using i128 = __int128;
int cnt[3];
i128 m;
i128 read(){
	i128 num=0;
	char c=getchar();
	while(c<'0' ||c>'9') c=getchar();
	while(c>='0' && c<='9'){
		num=num*10+c-'0';
		c=getchar();
	}
	return num;
}

void hanoi(i128 sum,int n,int from,int to,int tmp){
	//sum-总的执行次数 n-盘子数量 from-起点柱子 to-目标柱子 tmp-中转柱子
	if(sum==m) return ;//次数到了就结束
	i128 num=1;
	num=(num<<(n-1))-1;//计算(n-1)个盘子的移动次数 2^{n-1}-1
	if(sum+num>m){//m较小，递归模拟
		hanoi(sum,n-1,from,tmp,to);
		return ;
	}
	//上面n-1个盘子移动结束了，还没有m次,就直接整体移动，不用一步步模拟
	//n-1个从from 移动到tmp
	cnt[from]-=n-1;
	cnt[tmp]+=n-1;
	
	if(sum+num==m){//移动完n-1个后正好m次
		return ;
	}
	//1个 从 from 移动到 to
	cnt[from]--;
	cnt[to]++;
	
	if(sum+num+1==m){//移动完底下的正好m次
		return ;
	}
	// 上面两步移动完还没有m次，则递归模拟
	hanoi(sum+num+1,n-1,tmp,to,from);
}
int main(){
	i128 n;
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	while(1){
		n=read();
		m=read();
		if(n==0 && m==0) break;
		cnt[0]=n;cnt[1]=cnt[2]=0;
		if(n&1)
			hanoi(0,n,0,2,1);
		else
			hanoi(0,n,0,1,2);
		cout<<cnt[0]<<" "<<cnt[2]<<" "<<cnt[1]<<endl;
	}
	return 0;
}