树状数组讲解

1.引入

给出2个问题：

问题1：

问题2：

 

数据范围：

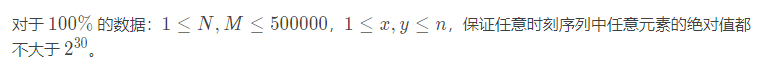
很显然，用 朴素的方法去模拟会超时，那么就需要一些更优秀的数据结构

——树状数组

2.基本概念

 

给出一个数组 a[8]={1,2,3,4,5,6,7,8}

然后看图

 

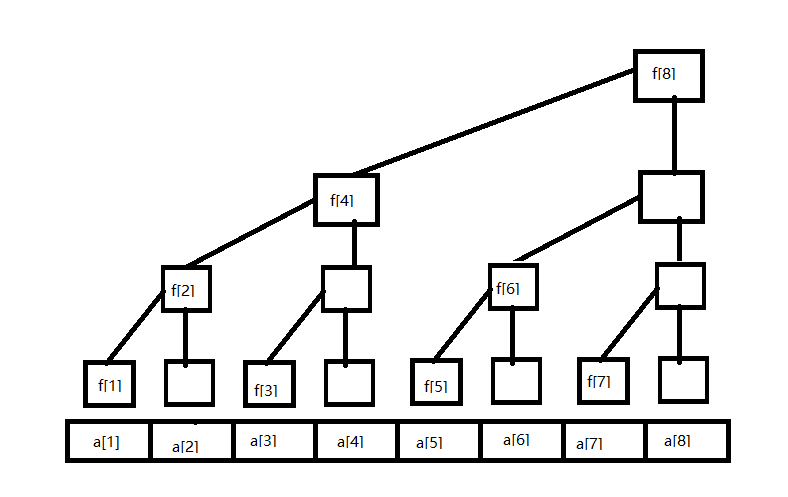
在如图的一棵二叉树中，f[1]=a[1],f[3]=a[3],f[5]=a[5],f[7]=a[7]

f[2]=a[1]+a[2],f[6]=a[5]+a[6]

f[4]=a[1]+a[2]+a[3]+a[4]

f[8]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]+a[8]

3.用法

（1）区间查询

如果将前i个元素的和记为sum[1]，那么通过这些值就可以把所有的sum[i]表示出来

比如:sum[7]=a[1]+a[2]+a[3]+a[4]+a[5]+a[6]+a[7]=f[4]+f[6]+f[7]

这里要介绍一下lowbit，lowbit(x)表示将x转为二进制后从右向左第一个1及后面的数字

比如7=(111)₂，那么lowbit(7)=001；6=(110)₂,那么lowbit(6)=010

再给出一个结论，lowbit(x)=x&(-x)，这里就不证明了，可以自己举例验证

然后我直接给出代码，结合代码理解

int sum(int x)
{
    int ans=0;
    while(x>0)
    {
        ans+=f[x];
        x-=lowbit(x); 
    }
    return ans;
}

当x=7时，先ans+=f[7]，这时lowbit(x)=(001)₂，x=x-lowbit(x)=(110)₂=6

然后ans+=f[6]，这时lowbit(x)=(010)₂，x=x-lowbit(x)=(100)₂=4

最后ans+=f[4]，这时lowbit(x)=(100)₂，x=x-lowbit(x)=(000)₂=0

循环结束

模拟代码可以得到，ans[7]=f[7]+f[6]+f[4]

然后就用前缀和的方法，区间[x,y]的和就是sum(y)-sum(x-1）

（2）单点修改

首先思考一个问题：当a[i]被改动时，有哪些f[]的值会变？

看那张图，可以发现当a[1]变时，f[1],f[2],f[4],f[8]会变；当a[3]变时，f[3],f[4],f[8]会变......

继续给出代码理解

void add(int x,int k)
{
    while(x<=n)
    {
        f[x]+=k;
        x+=lowbit(x);
    }
}

举x=3时的例子

先f[3]+=k，这时lowbit(x)=(001)₂，x=x+lowbit(x)=(100)₂=4

再f[4]+=k，这时lowbit(x)=(100)₂，x=x+lowbit(x)=(1000)₂=8

最后f[8]+=k，这时lowbit(x)=(1000)₂，x=x+lowbit(x)=(10000)₂=16

超出范围，循环结束

模拟代码可得，当a[3]变时，f[3],f[4],f[8]会变

其实基本框架已经讲完了......

（3）区间修改

前面两种操作都运用了前缀和，而接下来的两种操作就要用到差分

接下来的两种代码及思想都与之前有共同之处，所以解释相对简略

原数组每次读入时，减去前一个，再加到树状数组里，这样就差分了。

 

int la=0,a;
for(int i=1;i<=n;i++)
{
    cin>>a;
    add(i,a-la);
    la=a;
}
        

 

根据树状数组的性质，只需要前后节点都维护就行了。

用我的程序就是

void add(int x,int k)
{
    while(x<=n)
　　{
        f[x]+=k;
        x+=lowbit(x);
    }
}

add(x,k);
add(y+1,-k);

（4）单点查询

 因为我们用的是差分，差分的前缀就是原数组，该节点的结束值就是此时差分数组的前缀

所以代码就是

int sum(int x)
{
    int ans=0;
    while(x>0)
    {
        ans+=f[x];
        x-=lowbit(x); 
    }
    return ans;
}

cout<<ans(x)<<'\n';

4.关于树状数组

• 查询和修改的复杂度均为O(log n)
• 属于二进制的运用
• 是解决逆序对问题的常用方法

5.推荐例题

首先是“引入”里给出的两道模板题

https://www.luogu.com.cn/problem/P3374

https://www.luogu.com.cn/problem/P3368

以及一道逆序对题目

https://www.luogu.com.cn/problem/P1908