ST表讲解

1.引入

先给出一个问题

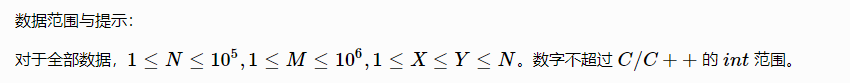
给出样例：

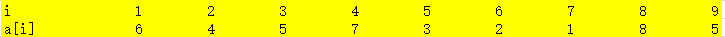
方法1：

看到这个问题，我的第一个想法是按题意根据每一个询问暴力找出区间最大值，但很明显这是会超时的。

方法2：

当然也有快一点的方法，可以先预处理，将所有可能的区间最大值全求出来，然后再询问时输出。

具体的话就是先把每相邻两个的最大值求出来，然后将[1,2]最大值和a₃比较可以得到[1,3]最大值，其余以此类推。

如果用f[x][y]表示区间[x,y]最大值，那么过程如图所示:

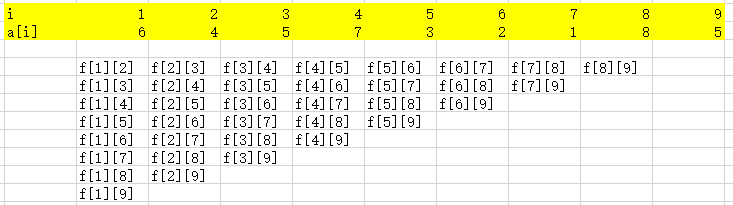
这样的时间和空间复杂度都为O（N²），任然无法通过此题。

2.ST表做法

方法3：

我们可以用如图所示的方法预处理：

 

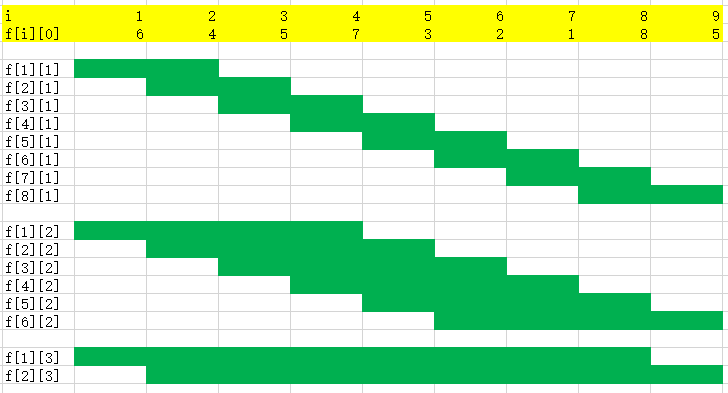
其中f[i][j]表示以i为起点，向右寻找2^j个元素得到的最大值，即[i,i+2^j-1]的最大值。

预处理的过程可以用dp解决，举个例子，如表，f[1][2]=max(f[1][1],f[3][1])，f[2][3]=max(f[2][2],f[6][2])

从特殊到一般可以得到:f[i][j]=max(f[i][j-1],f[i+2^j-1][j-1])。

询问的结果也可以用预处理出来的值得到，比如[1,6]的最大值为max(f[1][2],f[3][2]),[1,9]的最大值为max(f[1][3],f[2][3])

同样从特殊到一般可以得到:[x,y]的最大值为max(f[x][k],f[y-2^k+1][k])，其中k=log₂(y-x+1)向下取

这些结论可以通过表格去理解。

还剩一些细节，比如log怎么算？

这里给出一种做法，定义一个数组logn，将logn[0]设为-1，之后的每一项可以递推：logn[i]=logn[i/2]+1。

最后给出代码

#include <bits/stdc++.h>
using namespace std;
int f[200010][50],logn[200010]={-1}; 
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>f[i][0];
        logn[i]=logn[i/2]+1;
    }
    for(int j=1;j<=logn[n];j++)
        for(int i=1;i<=n-(1<<j)+1;i++)
            f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
    while(m--)
    {
        int x,y;
        cin>>x>>y;
        int k=logn[y-x+1];
        cout<<max(f[x][k],f[y-(1<<k)+1][k])<<endl;
    }
     return 0;
}

3.有关ST表

• 用于解决区间最值（RMQ）问题
• 时间复杂度为O(n log n)，其中每次询问的复杂度为O(1)，非常高效
• 只能处理静态区间最值，如果处理动态区间就要修改整张表
• 之后的树状数组和线段树可以维护动态区间